High School Geometry
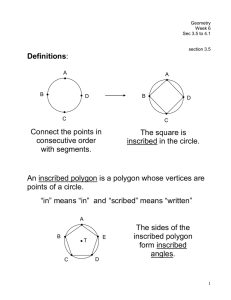
... Identify and describe relationships among inscribed angles, radii, and chords. (MA10‐GR.HS‐S.4‐GLE.2‐EO.e.i) (CCSS: G‐C.2) PARCC Calculator Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is p ...
... Identify and describe relationships among inscribed angles, radii, and chords. (MA10‐GR.HS‐S.4‐GLE.2‐EO.e.i) (CCSS: G‐C.2) PARCC Calculator Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is p ...
Key Learning in Mathematics - Year 6
... Recognise, describe and build simple 3-D shapes, including making nets Recognise angles where they meet at a point, are on a straight line, or are vertically opposite, and find missing angles Find unknown angles in any triangles, quadrilaterals, regular polygons ...
... Recognise, describe and build simple 3-D shapes, including making nets Recognise angles where they meet at a point, are on a straight line, or are vertically opposite, and find missing angles Find unknown angles in any triangles, quadrilaterals, regular polygons ...
Plane Geometry
... A circle is defined as a closed plane curve every point of which is equidistant from a fixed point within the curve. ...
... A circle is defined as a closed plane curve every point of which is equidistant from a fixed point within the curve. ...
Name: :______ Date:
... 4. Use right triangle trigonometry to explain the relationship between the angle and the highlighted leg of the right triangle in the unit circle. What trigonometric function can be represented by the length of the leg of the right triangle? ...
... 4. Use right triangle trigonometry to explain the relationship between the angle and the highlighted leg of the right triangle in the unit circle. What trigonometric function can be represented by the length of the leg of the right triangle? ...