A semi-reflexive tactic for (sub-)equational reasoning
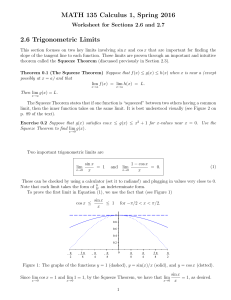
... Relations or simply PERs) can be used in type theory to reason about functions over equivalence classes over a subset of a given set X: let (X, ≡) be a set together with a PER over it. We say that an element x ∈ X is proper if x ≡ x. The subset of the proper elements of X forms a setoid. To represen ...
... Relations or simply PERs) can be used in type theory to reason about functions over equivalence classes over a subset of a given set X: let (X, ≡) be a set together with a PER over it. We say that an element x ∈ X is proper if x ≡ x. The subset of the proper elements of X forms a setoid. To represen ...
Section 4.1: The Definite Integral
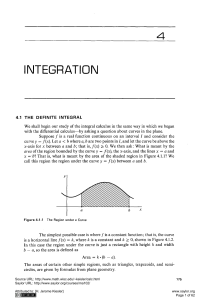
... with the differential calculus-by asking a question about curves in the plane. Suppose f is a real function continuous on an interval I and consider the curve y = f(x). Let a < b where a, bare two points in J, and let the curve be above the x-axis for x between a and b; that is, f(x) ~ 0. We then as ...
... with the differential calculus-by asking a question about curves in the plane. Suppose f is a real function continuous on an interval I and consider the curve y = f(x). Let a < b where a, bare two points in J, and let the curve be above the x-axis for x between a and b; that is, f(x) ~ 0. We then as ...
2012_0080. Introduction to MV logic
... • Second, MV logic is used in some top EDA tools as mathematical technique to minimize binary logic (Synopsys, Cadence, Lattice) • Thirdly, MV logic can be realized in software and as such is used in Machine Learning, Artificial Intelligence, Data Mining, and Robotics ...
... • Second, MV logic is used in some top EDA tools as mathematical technique to minimize binary logic (Synopsys, Cadence, Lattice) • Thirdly, MV logic can be realized in software and as such is used in Machine Learning, Artificial Intelligence, Data Mining, and Robotics ...
Function of several real variables
In mathematical analysis, and applications in geometry, applied mathematics, engineering, natural sciences, and economics, a function of several real variables or real multivariate function is a function with more than one argument, with all arguments being real variables. This concept extends the idea of a function of a real variable to several variables. The ""input"" variables take real values, while the ""output"", also called the ""value of the function"", may be real or complex. However, the study of the complex valued functions may be easily reduced to the study of the real valued functions, by considering the real and imaginary parts of the complex function; therefore, unless explicitly specified, only real valued functions will be considered in this article.The domain of a function of several variables is the subset of ℝn for which the function is defined. As usual, the domain of a function of several real variables is supposed to contain an open subset of ℝn.