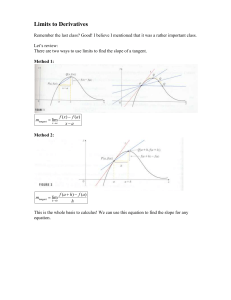
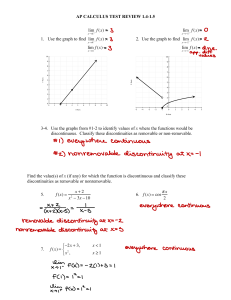
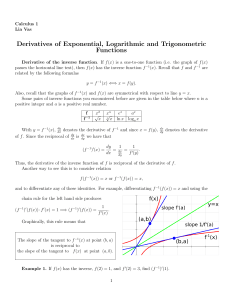
On Malliavin`s proof of Hörmander`s theorem
... In view of this S result, Hörmander’s condition is not surprising. Indeed, if we define E(x,t) = k≥0 V̂k (x, t), then this gives us a subbundle of Rn+1 which is integrable by construction of the V̂k . Note that the dimension of E(x,t) could in principle depend on (x, t), but since the dimension is ...
... In view of this S result, Hörmander’s condition is not surprising. Indeed, if we define E(x,t) = k≥0 V̂k (x, t), then this gives us a subbundle of Rn+1 which is integrable by construction of the V̂k . Note that the dimension of E(x,t) could in principle depend on (x, t), but since the dimension is ...
Limit worksheets - Canvas
... Instructor’s overview – 2 The problems used in the slides below are indicative what level we expect throughout the course. Instructors will want to supplement these with both easier and harder examples as class progress dictates. One goal in providing these templates is to help ensure a uniform lev ...
... Instructor’s overview – 2 The problems used in the slides below are indicative what level we expect throughout the course. Instructors will want to supplement these with both easier and harder examples as class progress dictates. One goal in providing these templates is to help ensure a uniform lev ...
Factorials of real negative and imaginary numbers - A
... important contributions to derive several important properties of the gamma function (Srinivasan 2007). Anglani and Barlie (2007) gave the additive representation of factorials. The gamma function is extended to all complex numbers, with a real part >0, except for at zero and negative integers. Figu ...
... important contributions to derive several important properties of the gamma function (Srinivasan 2007). Anglani and Barlie (2007) gave the additive representation of factorials. The gamma function is extended to all complex numbers, with a real part >0, except for at zero and negative integers. Figu ...
Function of several real variables
In mathematical analysis, and applications in geometry, applied mathematics, engineering, natural sciences, and economics, a function of several real variables or real multivariate function is a function with more than one argument, with all arguments being real variables. This concept extends the idea of a function of a real variable to several variables. The ""input"" variables take real values, while the ""output"", also called the ""value of the function"", may be real or complex. However, the study of the complex valued functions may be easily reduced to the study of the real valued functions, by considering the real and imaginary parts of the complex function; therefore, unless explicitly specified, only real valued functions will be considered in this article.The domain of a function of several variables is the subset of ℝn for which the function is defined. As usual, the domain of a function of several real variables is supposed to contain an open subset of ℝn.