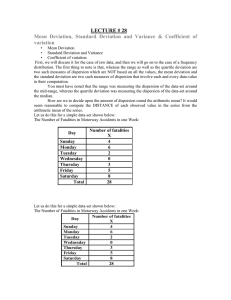
LECTURE # 28 Mean Deviation, Standard Deviation and Variance
... SHORT CUT FORMULA OF THE STANDARD DEVIATION IN CASE OF GROUPED ...
... SHORT CUT FORMULA OF THE STANDARD DEVIATION IN CASE OF GROUPED ...
AP Statistics Review Normal Models and Sampling Distributions
... 2.0 liters, but extra room at the top of the bottle allows for a maximum of 2.25 liters of soda before the bottle overflows. The standard deviation of the amount of soda put into the bottles by the machine is known to be 0.15 liter. (a) Overfilling the bottles causes a mess on the assembly line, but ...
... 2.0 liters, but extra room at the top of the bottle allows for a maximum of 2.25 liters of soda before the bottle overflows. The standard deviation of the amount of soda put into the bottles by the machine is known to be 0.15 liter. (a) Overfilling the bottles causes a mess on the assembly line, but ...
Estimating (D3)
... 3) For large sample sizes, the sampling distribution of the mean may be approximated by a normal distribution. This approximation improves as the size of the samples increases: The three properties of sampling distribution given above together comprise the Central Limit Theorem. Example 1.3: Suppose ...
... 3) For large sample sizes, the sampling distribution of the mean may be approximated by a normal distribution. This approximation improves as the size of the samples increases: The three properties of sampling distribution given above together comprise the Central Limit Theorem. Example 1.3: Suppose ...
Statistics for Business and Economics, 6/e
... To find the average score it is necessary to calculate the total scores tor all students. For this, the multiplication between the score and the frequency To find the average score it is necessary to calculate the total scores tor all students. For this, the multiplication between the score and the ...
... To find the average score it is necessary to calculate the total scores tor all students. For this, the multiplication between the score and the frequency To find the average score it is necessary to calculate the total scores tor all students. For this, the multiplication between the score and the ...
Decile Mean: A New Robust Measure of Central Tendency
... evidence that they may perform poorly in the presence of non-normality or when outliers occur in data. We investigate the performances of some popular and commonly used measures of central tendency such as the mean, the median and the trimmed mean and observe that they may not perform as good as we ...
... evidence that they may perform poorly in the presence of non-normality or when outliers occur in data. We investigate the performances of some popular and commonly used measures of central tendency such as the mean, the median and the trimmed mean and observe that they may not perform as good as we ...
Measures of Dispersion
... Quartile deviation considers only 50% of the item and ignores the other 50% of items in the series. Mean deviation no doubt an improved measure but ignores negative signs without any basis. Karl Pearson after observing all these things has given us a more scientific formula for calculating or measur ...
... Quartile deviation considers only 50% of the item and ignores the other 50% of items in the series. Mean deviation no doubt an improved measure but ignores negative signs without any basis. Karl Pearson after observing all these things has given us a more scientific formula for calculating or measur ...
Chapter 7 and Chapter 8 Practice
... 8) A coffee machine dispenses normally distributed amounts of coffee with a mean of 12 ounces and a standard deviation of 0.2 ounce. If a sample of 9 cups is selected, find the probability that the mean of the sample will be less than 12.1 ounces. Find the probability if the sample is just 1 cup. Us ...
... 8) A coffee machine dispenses normally distributed amounts of coffee with a mean of 12 ounces and a standard deviation of 0.2 ounce. If a sample of 9 cups is selected, find the probability that the mean of the sample will be less than 12.1 ounces. Find the probability if the sample is just 1 cup. Us ...