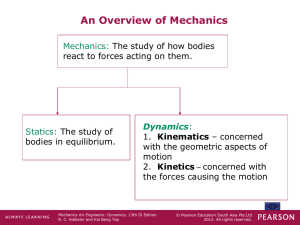
week 1
... The t-axis is tangent to the path (curve) at the instant considered, positive in the direction of the particle’s motion. The n-axis is perpendicular to the t-axis with the positive direction toward the center of curvature of the curve. Mechanics for Engineers: Dynamics, 13th SI Edition R. C. Hibbele ...
... The t-axis is tangent to the path (curve) at the instant considered, positive in the direction of the particle’s motion. The n-axis is perpendicular to the t-axis with the positive direction toward the center of curvature of the curve. Mechanics for Engineers: Dynamics, 13th SI Edition R. C. Hibbele ...
Revisiting a 90yearold debate: the advantages of the mean deviation
... science. The first is concerned with the Platonic world of perfect distributions and ideal measurements. Perhaps agriculture, where Fisher worked and where vegetative reproduction of cases is possible, is one of the fields that most closely approximates this world. The second is concerned with the A ...
... science. The first is concerned with the Platonic world of perfect distributions and ideal measurements. Perhaps agriculture, where Fisher worked and where vegetative reproduction of cases is possible, is one of the fields that most closely approximates this world. The second is concerned with the A ...
Sample pages 2 PDF
... These two equations cannot be integrated, because their left hand sides do not represent total differentials of some functions. Consequently, they provide an example of a non-holonomic (vector) constraint. There are no general methods of solving problems involving non-holonomic constraints. Each cas ...
... These two equations cannot be integrated, because their left hand sides do not represent total differentials of some functions. Consequently, they provide an example of a non-holonomic (vector) constraint. There are no general methods of solving problems involving non-holonomic constraints. Each cas ...
Connected Particles
... This icon indicates the slide contains activities created in Flash. These activities are not editable. For more detailed instructions, see the Getting Started presentation. 11 of of 67 ...
... This icon indicates the slide contains activities created in Flash. These activities are not editable. For more detailed instructions, see the Getting Started presentation. 11 of of 67 ...
Classical Electrodynamics and Theory of Relativity
... processes, this was theory of electromagnetism. Development of theory of electromagnetism in XIX-th century became a premise for arising theory of relativity. In this book I follow historical sequence of events. In Chapter I electrostatics and magnetostatics are explained starting with first experim ...
... processes, this was theory of electromagnetism. Development of theory of electromagnetism in XIX-th century became a premise for arising theory of relativity. In this book I follow historical sequence of events. In Chapter I electrostatics and magnetostatics are explained starting with first experim ...
Social Science Reasoning Using Statistics
... – Value most representative of the entire distribution, that is, of all of the individuals – Central Tendency: 3 main measures – Mean (M) – Median (Mdn) – Mode • Note: “Average” may refer to each of these three measures, but it usually refers to Mean. ...
... – Value most representative of the entire distribution, that is, of all of the individuals – Central Tendency: 3 main measures – Mean (M) – Median (Mdn) – Mode • Note: “Average” may refer to each of these three measures, but it usually refers to Mean. ...
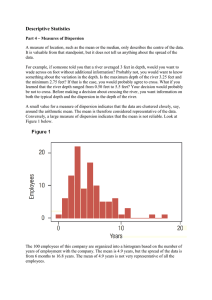
Descriptive Statistics
... The mean deviation has two advantages. First, it uses all the values in the computation whereas the range uses only the highest and the lowest values. Second, it is easy to understand - it is the average amount by which values deviate from the mean. However, its drawback is the use of absolute value ...
... The mean deviation has two advantages. First, it uses all the values in the computation whereas the range uses only the highest and the lowest values. Second, it is easy to understand - it is the average amount by which values deviate from the mean. However, its drawback is the use of absolute value ...
Multiple Choice Questions Descriptive Statistics
... where L indicates that the earthquake had an intensity below 4.0 and a H indicates that the earthquake had an intensity above 9.0. One measure of central tendancy is the x% trimmed mean computed after trimming x% of the upper values and x% of the bottom values. The value of the 20% trimmed mean is: ...
... where L indicates that the earthquake had an intensity below 4.0 and a H indicates that the earthquake had an intensity above 9.0. One measure of central tendancy is the x% trimmed mean computed after trimming x% of the upper values and x% of the bottom values. The value of the 20% trimmed mean is: ...
Mean and median - ESE - Salento University Publishing
... distributions β equals one. So the expectation value of the squared difference between mean and median is of the order of the variance of the mean for both normal and uniform distributions. From Chebyshev’s inequality it can be derived that the difference between mean and median of a continuous pr ...
... distributions β equals one. So the expectation value of the squared difference between mean and median is of the order of the variance of the mean for both normal and uniform distributions. From Chebyshev’s inequality it can be derived that the difference between mean and median of a continuous pr ...