* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Random Number Generation
Multiplication algorithm wikipedia , lookup
Horner's method wikipedia , lookup
Mean field particle methods wikipedia , lookup
Monte Carlo method wikipedia , lookup
Newton's method wikipedia , lookup
Simulated annealing wikipedia , lookup
False position method wikipedia , lookup
Resampling (statistics) wikipedia , lookup
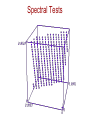
Random Number Generation Fall 2013 By Yaohang Li, Ph.D. Review • Last Class – Variance Reduction • This Class – – – – Random Number Generation Uniform Distribution Non-uniform Distribution Random Number Generation Assignment 3 • Next Class – Quasi-Monte Carlo Random Numbers • Application of Random Numbers – Simulation • Simulate natural phenomena – Sampling • It is often impractical to examine all possible cases, but a random sample will provide insight into what constitutes typical behavior – Numerical analysis – Computer programming – Decision making • “Many executives make their decisions by flipping a coin…” – Recreation Natural Random Number • Natural Random Numbers – No two snowflakes are the same – Sources • White Noise • Water Molecule Distribution • etc. – Generation • Measurement • Irreproducible • Errors Pseudorandom Number Generators • Pseudorandom Numbers – Using a Mathematical Formula – Deterministic – Behave like real random numbers • Comments – There is no “perfect” pseudorandom number generator – We should never completely trust results from a single pseudorandom number generator – Good random number generators are hard to find Middle-square method • Developed by von Neumann • Procedure – 4 digit starting value is created – Square and produce 8-digit number – Get the middle 4 digits as the result and seed for next number • Problems – What if the middle 4 digits are 0 – Forsythe found that the sequence may stuck in 6100, 2100, 4100, 8100, 6100, … • Not a good generator Quality of Pseudorandom Numbers • • • • • • • Uniformity Randomness Independence Reproducibility Portability Efficiency A sufficiently long period Generating Uniform Random Numbers • Generating Uniform Random Numbers – Uniform distribution on [0,1) – Generation • Un=Xn/m – Xn: Random number Integer – m: Max(Xn)+1: Usually the word size of a computer – Un: Uniform real random number at [0,1) Linear Congruential Method • Linear Congruential Method – Most commonly used generator for pseudorandom numbers xn axn1 b (mod m) • m: modulus • a: multiplier • b: additive constant – Period • m constrains the period – max period: 2m-1 – m is usually chosen to be either prime of a power-of-two Shift-Register Generators (SRG) • Shift-Register Generators – based on the following recursion k 1 xnk ai xni (mod 2), i 0 – ai and xi are either 0 or 1 – Comments • The recursion produces only bits • Incorporate these bits into integers Lagged-Fibonacci Generators • Lagged-Fibonacci Generators (LFG) – Additive Lagged-Fibonacci Generators xn xn j xnk (mod 2m ), j k – Multiplicative Lagged-Fibonacci Generators xn xn j xnk (mod 2m ), j k • Comments – LFG has a much longer period than LCGs – (2k-1)2m-1 Spectral Tests Spectral Tests Inversive Congruential Generators • Inversive Congruential Generators (ICGs) – Recursive ICGs xn a x n1 b (mod m), – Explicit ICGs xn an b (mod m) cc 1 (mod m) – Advantage of ICGs • ICGs do not fall in hyperplanes Combined Generators • Combined Generators – Combining different recurrences can increase the period length – Improve the structural properties of pseudorandom generators – Construct a new random sequence z n xn y n , – • exclusive-or operator • addition modulo • addition of floating-point random numbers modulo 1 – x, y • Different random number sources Parallel Random Number Generators • Requirements of Parallel Random Numbers – Every random number sequence generated on each processor should satisfy the requirements of a good sequential generator. – The parallel generator must be reproducible both on different machines and on the same machine with a different partitioning of the processing resources. – The parallelly generated random streams must be uncorrelated and must not overlap. – The parallel generator should work for an arbitrary, but perhaps bounded, number of processors. Parallel Random Numbers Generations (Leapfrog) • Leapfrog Parallel Random Numbers Generations (Sequence Splitting) • Sequence Splitting Parallel Random Numbers Generations (Sequence Splitting) • Random Tree Method – Also called parameterization method SPRNG • http://sprng.cs.fsu.edu Random Choices from a Finite Set •A random integer X between 0 and k-1 X kU – U is a random number uniformly distributed in [0,1) •A more general case x1 , if 0 U p1 X x2 , ifp1 U p1 p2 x , ifp p ... p U 1 2 k k 1 Inverse Function Method • Cumulative Distribution Function – Most real-valued distribution may be expressed in terms of its distribution function F(x) • Inverse Function Method – X=F-1(U) – Now the problem reduces to how to evaluate the inverse function F-1() Interesting Trick • Generating the random samples of F(x)=x2 • Inverse Function Method – X=U-1/2 • A short cut method – If X1 is a random variable having the distribution F1(x) and if X2 is a random variable having the distribution F2(x) • max(X1, X2) has the distribution F1(x)F2(x) • min(X1, X2) has the distribution F1(x)+F2(x)-F1(x)F2(x) – Then X=max(U1, U2) has the distribution of F(x)=x2 – Hard to believe that max(U1, U2) and U-1/2 have the same distribution Normal Distribution • Polar Method 1. 2. 3. 4. 5. Generate two independent random variables, U1 and U2 Set V1=2U1-1, V2=2U2-1 Set S=V1*V1+V2*V2 If S>=1, return to Step 1 Set X1 and X2 according to the following two equations X 1 V1 2 ln S S X 2 V2 2 ln S S Acceptance-Rejection Method • Desired pdf – • Suppose we bound the desired probability distribution function to sample from a box Algorithm 1. Generate a random variable x from U(0,1) 2. Generate another random variable y from U(0,1) 3. If x<f(y)/fmax then return y 4. else repeat from step 1 Acceptance-Rejection Method Example • Determine an algorithm for generating random variates for a random variable that take values 1, 2, …, 10 with probabilities 0.11, 0.12, 0.09, 0.08, 0.12, 0.10, 0.09, 0.09. 0.10, 0.10 respectively • Acceptance-Rejection Method – u1=U(0,1), u2=U(0,1), c=max(p())=0.12 – Y=floor(10*u1+1) – while (u2>p(Y)/c) • u1=U(0,1), u2=U(0,1) • Y=floor(10*u1+1) – output Y Analysis of Acceptance-Rejection Method • Advantage – Acceptance-Rejection Method can fit in different pdfs – popularly used in complicated probability geometry • Disadvantage – Inefficient if the volume of the region of interest is small relative to that of the box • most of the darts will miss the target Exponential Distribution • F(x)=1-e-x/ – Logarithm method (inverse function method) – X=-lnU Shuffling Algorithm • Let X1, X2, …, Xt be a set of t numbers to be shuffled 1. 2. 3. 4. 5. j=t Generate U Set k=floor (jU)+1 Exchange Xk with Xj Decrease j by 1. If j>1, return to step 2 • Random Numbers Summary – Uniform Random Numbers • Generation of Uniform Random Numbers – Natural Random Number Generators – Pseudorandom Number Generators • Pseudorandom Number Generators – – – – – – Requirement of Pseudorandom Number Generators LCG LFG SRG ICG Combined Random Number Generators • Parallel Random Number Generators – Requirement of Parallel Random Number Generators – Techniques for Parallel Random Number Generators • Leapfrog • Sequence Splitting • Random Tree Summary • Numerical Distribution – Random Choices from a finite set – General methods for continuous distributions • inverse function method • acceptance-rejection method – Distributions • Normal distribution – Polar method • Exponential distribution – Shuffling What I want you to do? • Review Slides • Review basic probability/statistics concepts