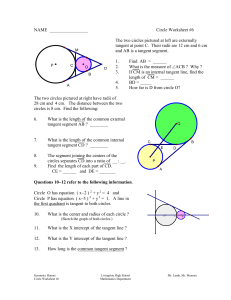
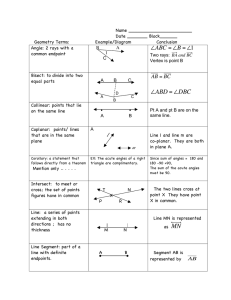
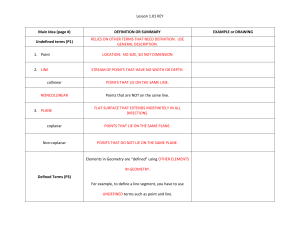
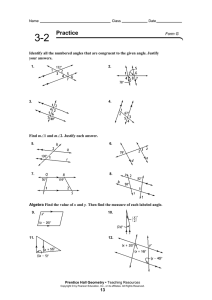
Homework sheet 6
... (where N = mn + m + n) is injective, with image equal to an algebraic set in PN (Ω). [This was asserted in class; your job is to check it carefully.] 3. Consider the projective plane curve C cut out by the homogeneous equation Y 2 Z = X 2 (X + Z). Write down a non-constant morphism from P1 to C; car ...
... (where N = mn + m + n) is injective, with image equal to an algebraic set in PN (Ω). [This was asserted in class; your job is to check it carefully.] 3. Consider the projective plane curve C cut out by the homogeneous equation Y 2 Z = X 2 (X + Z). Write down a non-constant morphism from P1 to C; car ...
Year 7 - Nrich
... The interactive workout generates questions on a variety of core topics, complete with solutions, which could be used as lesson starters or for revision. Iffy Logic, Contrary Logic and Twisty Logic provide a good grounding in the logical reasoning needed in A Level Mathematics. ...
... The interactive workout generates questions on a variety of core topics, complete with solutions, which could be used as lesson starters or for revision. Iffy Logic, Contrary Logic and Twisty Logic provide a good grounding in the logical reasoning needed in A Level Mathematics. ...
Vectors 1 - Core 4 Revision 1. The lines L and M have vector
... The lines l1 and l2 have vector equations r = (2 + λ)i + (–2 – λ)j + (7 + λ)k and r = (4 + 4µ)i + (26 + 14µ)j + (–3 – 5µ)k respectively, where λ and µ are scalar parameters. ...
... The lines l1 and l2 have vector equations r = (2 + λ)i + (–2 – λ)j + (7 + λ)k and r = (4 + 4µ)i + (26 + 14µ)j + (–3 – 5µ)k respectively, where λ and µ are scalar parameters. ...
Lesson 1.01 KEY Main Idea (page #) DEFINITION OR SUMMARY
... Flat surface that extends infinitely and has no depth. All the points are a given distance, the radius, from a given ...
... Flat surface that extends infinitely and has no depth. All the points are a given distance, the radius, from a given ...
When is Tangent, tangent? - TI Education
... activity screens are set up for handheld view and may need re-positioning in computer view. Scaling view to 200% can assist when grabbing points in the activity. TI-Nspire Applications Notes (with Q&A), Calculator, L&S, G&G. ...
... activity screens are set up for handheld view and may need re-positioning in computer view. Scaling view to 200% can assist when grabbing points in the activity. TI-Nspire Applications Notes (with Q&A), Calculator, L&S, G&G. ...
0025_hsm11gmtr_1203.indd
... in Washington, D.C. Your binoculars are at the vertex of the angle formed by tangents to the dome. You estimate that this vertex angle is 70. What is the measure of the arc of the circular base of the dome that is visible? Find the diameter of O. A line that appears to be tangent is tangent. If you ...
... in Washington, D.C. Your binoculars are at the vertex of the angle formed by tangents to the dome. You estimate that this vertex angle is 70. What is the measure of the arc of the circular base of the dome that is visible? Find the diameter of O. A line that appears to be tangent is tangent. If you ...
Handout #5 AN INTRODUCTION TO VECTORS Prof. Moseley
... = [3/5, 4/5] . To make vectors in ú more applicable to two dimensional geometry we can introduce the concept of an equivalence relation and equivalence classes. We say that an arbitrary directed line segment in the p lane is equivalent to a geometrical vector in G if it has the same direction and ma ...
... = [3/5, 4/5] . To make vectors in ú more applicable to two dimensional geometry we can introduce the concept of an equivalence relation and equivalence classes. We say that an arbitrary directed line segment in the p lane is equivalent to a geometrical vector in G if it has the same direction and ma ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.