S1-Equivariant K-Theory of CP1
... dimensional vector spaces, we call E = tx∈X Ex a G -vector bundle if it is equipped with certain topological structure and a continuous action of G such that g .Ex = Eg .x . Example. (The Hopf Bundle) A canonical example of a S 1 -bundle over CP1 is H ∗ := {([d], z) ∈ CP1 × C2 : z is a point in the ...
... dimensional vector spaces, we call E = tx∈X Ex a G -vector bundle if it is equipped with certain topological structure and a continuous action of G such that g .Ex = Eg .x . Example. (The Hopf Bundle) A canonical example of a S 1 -bundle over CP1 is H ∗ := {([d], z) ∈ CP1 × C2 : z is a point in the ...
Lecture 8: Curved Spaces
... side of the Einstein equation is related to the Riemann curvature tensor which is obtained by parallel transporting a vector around a parallelogram just like for two dimensional surfaces. Lastly a few words about the energy-momentum tensor. For simple systems (e.g. a system of dust particles) this t ...
... side of the Einstein equation is related to the Riemann curvature tensor which is obtained by parallel transporting a vector around a parallelogram just like for two dimensional surfaces. Lastly a few words about the energy-momentum tensor. For simple systems (e.g. a system of dust particles) this t ...
0002_hsm11gmtr_0301.indd
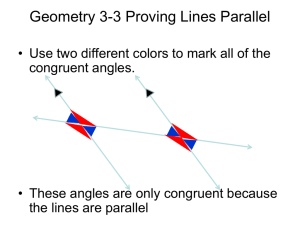
... north to south. Are the bridge and the highway parallel, skew, or neither? Explain. ...
... north to south. Are the bridge and the highway parallel, skew, or neither? Explain. ...
Week 5
... • Calculate using the Pythagoreon Theorem, sin, and cos • Calculate the components of a force vector • Add two force vectors together • Understand the concept of equilibrium • Calculate reactions • Determine if a truss is stable ...
... • Calculate using the Pythagoreon Theorem, sin, and cos • Calculate the components of a force vector • Add two force vectors together • Understand the concept of equilibrium • Calculate reactions • Determine if a truss is stable ...
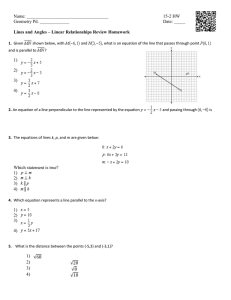
Geometry Proving Lines are Parallel Worksheet ⋆Algebra For #1
... ?Algebra For #1-3, find the value of x that makes m k n. ...
... ?Algebra For #1-3, find the value of x that makes m k n. ...
Chapter 5
... If you stand on a scale while riding an elevator, how would your weight differ from normal in the following situations? The elevator accelerates upward from rest. The elevator accelerates downward from rest. The elevator slows while going up. The elevator slows while going down. The elevator moves a ...
... If you stand on a scale while riding an elevator, how would your weight differ from normal in the following situations? The elevator accelerates upward from rest. The elevator accelerates downward from rest. The elevator slows while going up. The elevator slows while going down. The elevator moves a ...
Geometry Notes
... Geometry Notes Lesson 5.3A – Trigonometry T.2.G.6 Use trigonometric ratios (sine, cosine, tangent) to determine lengths of sides and measures of angles in right triangles including angles of elevation and angles of depression T.2.G.7 Use similarity of right triangles to express the sine, cosine, and ...
... Geometry Notes Lesson 5.3A – Trigonometry T.2.G.6 Use trigonometric ratios (sine, cosine, tangent) to determine lengths of sides and measures of angles in right triangles including angles of elevation and angles of depression T.2.G.7 Use similarity of right triangles to express the sine, cosine, and ...
Geometry review, part I Geometry review I
... ignored), but we have different properties. In 2D, the vector perpendicular to a given vector is unique (up to a scale). In 3D, it is not. Two 3D vectors in 3D can be multiplied to get a vector (vector or cross product). Dot product works the same way, but the coordinate expression is (v·w) = vxwx+ ...
... ignored), but we have different properties. In 2D, the vector perpendicular to a given vector is unique (up to a scale). In 3D, it is not. Two 3D vectors in 3D can be multiplied to get a vector (vector or cross product). Dot product works the same way, but the coordinate expression is (v·w) = vxwx+ ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.