Geometry Name: Introduction to Proofs: Theorems and Postulates
... consecutive interior angles are supplementary. If two parallel lines are cut by a transversal, then consecutive exterior angles are supplementary. If two parallel lines are cut by a transversal, then corresponding angles are congruent, alternate interior angles are congruent, and alternate exterior ...
... consecutive interior angles are supplementary. If two parallel lines are cut by a transversal, then consecutive exterior angles are supplementary. If two parallel lines are cut by a transversal, then corresponding angles are congruent, alternate interior angles are congruent, and alternate exterior ...
File
... Theorem 5.3 – angle bisector theorem - if a point is on the bisector of an angle, then it is equidistant from the sides of the angle Theorem 5.4 – converse of the angle bisector theorem - if a point is equidistant from the sides of an angle, then it is on the angle bisector theorem 5.5 - The p ...
... Theorem 5.3 – angle bisector theorem - if a point is on the bisector of an angle, then it is equidistant from the sides of the angle Theorem 5.4 – converse of the angle bisector theorem - if a point is equidistant from the sides of an angle, then it is on the angle bisector theorem 5.5 - The p ...
Module 3 Homework Answers
... Topic: Rotational symmetry Hubcaps have rotational symmetry. That means that a hubcap does not have to turn a full circle to appear the same. For instance, a hubcap with this pattern, , will look the same every turn. It is said to have 90 rotational symmetry because for each quarter turn it rotates ...
... Topic: Rotational symmetry Hubcaps have rotational symmetry. That means that a hubcap does not have to turn a full circle to appear the same. For instance, a hubcap with this pattern, , will look the same every turn. It is said to have 90 rotational symmetry because for each quarter turn it rotates ...
geometry unit 2 workbook
... For 7-13, fill in the blanks with always, sometimes, or never. 7. A Rhombus is ________________ equilateral. 8. The diagonals of a rectangle are ________________ perpendicular. 9. A rectangle is ________________ a rhombus. 10) A parallelogram is ________________ a rhombus. 11) A square is __________ ...
... For 7-13, fill in the blanks with always, sometimes, or never. 7. A Rhombus is ________________ equilateral. 8. The diagonals of a rectangle are ________________ perpendicular. 9. A rectangle is ________________ a rhombus. 10) A parallelogram is ________________ a rhombus. 11) A square is __________ ...
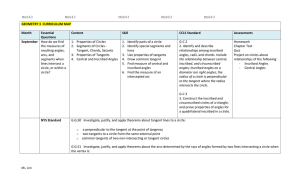
Subject Geometry Academic Grade 10 Unit # 2 Pacing 8
... In Unit 2 students will thoroughly study the properties of triangles. Students will be able to identify congruent triangles, write congruence statements, and apply theorems to prove triangles congruent. Students will also study the properties of quadrilaterals and be able to identify the different q ...
... In Unit 2 students will thoroughly study the properties of triangles. Students will be able to identify congruent triangles, write congruence statements, and apply theorems to prove triangles congruent. Students will also study the properties of quadrilaterals and be able to identify the different q ...
Solutions to in-class problems
... = AC. By the Existence and Uniqueness of Perpendiculars, we can drop a perpendicular from A to some point P on BC. Then, since ∠ABC ∼ ...
... = AC. By the Existence and Uniqueness of Perpendiculars, we can drop a perpendicular from A to some point P on BC. Then, since ∠ABC ∼ ...
Shape Blending Using the Star-Skeleton Representation - CS
... are visible. The star-skeleton is comprised of two parts: a decomposition of the polygon into star-shaped pieces, each represented by its vertices and a special star point called the star origin (upper part of Figure 1); and a planar graph, the skeleton, that joins the star origins (lower part of Fi ...
... are visible. The star-skeleton is comprised of two parts: a decomposition of the polygon into star-shaped pieces, each represented by its vertices and a special star point called the star origin (upper part of Figure 1); and a planar graph, the skeleton, that joins the star origins (lower part of Fi ...
Target 5a (Day 1)
... equidistant from the ______________ of the segment. Theorem 5.2 – Any point _________________ from the endpoints of a segment _______ on the perpendicular bisector of the segment. Concurrent lines – When ___ or more lines intersect at a common point. Point of Concurrency – The ________________ point ...
... equidistant from the ______________ of the segment. Theorem 5.2 – Any point _________________ from the endpoints of a segment _______ on the perpendicular bisector of the segment. Concurrent lines – When ___ or more lines intersect at a common point. Point of Concurrency – The ________________ point ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑