Solving Linear Diophantine Equations Using the Geometric
... Given a system of linear Diophantine equations A1 x1 +. . .+An xn = 0, which we shall write as AX = 0, each Ai denoting the ith column of A, we suppose, without loss of generality, that A is a full row rank m×n integral matrix. Let S0 (A) denote the set of minimal solutions of minimal support, and L ...
... Given a system of linear Diophantine equations A1 x1 +. . .+An xn = 0, which we shall write as AX = 0, each Ai denoting the ith column of A, we suppose, without loss of generality, that A is a full row rank m×n integral matrix. Let S0 (A) denote the set of minimal solutions of minimal support, and L ...
Full text
... lim B(t) = lim C(t) = 1. Remark: In [2], similar recurrences are treated by a slightly different method. The recursion for (qn) can be considered as a fixed-point problem and our results can be derived in principal by studying this fixed-point problem. ...
... lim B(t) = lim C(t) = 1. Remark: In [2], similar recurrences are treated by a slightly different method. The recursion for (qn) can be considered as a fixed-point problem and our results can be derived in principal by studying this fixed-point problem. ...
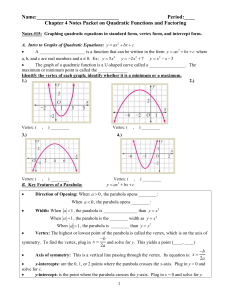
Day 57 - 61 EOC Quadratics Reivew
... 2nd: Factor out the GCF 3rd: Complete the X & box method to find the factors 4th: Set every factor that contains an x in it, equal to 0 & solve for x. B.) Completing the Square 1st: Move the constant (number with no variable) to the right so that all variables are on the left & all constants are on ...
... 2nd: Factor out the GCF 3rd: Complete the X & box method to find the factors 4th: Set every factor that contains an x in it, equal to 0 & solve for x. B.) Completing the Square 1st: Move the constant (number with no variable) to the right so that all variables are on the left & all constants are on ...
Literal Equations Manipulating Variables and Constants
... the products ma or πr2. In this case the unknown (such as r in πr2) must factored out of the term before we can isolate it. The following rules, examples, and exercises will help you review and practice solving literal equations from physics and chemistry. PROCEDURE In general, we solve a literal eq ...
... the products ma or πr2. In this case the unknown (such as r in πr2) must factored out of the term before we can isolate it. The following rules, examples, and exercises will help you review and practice solving literal equations from physics and chemistry. PROCEDURE In general, we solve a literal eq ...
5.2 Vertex Form
... It’s a simple matter to transform the equation f (x) = (x + 2)2 + 3 into the general form of a quadratic function, f (x) = ax2 + bx + c. We simply use the three-step algorithm to square the binomial; then we combine like terms. f (x) = (x + 2)2 + 3 f (x) = x2 + 4x + 4 + 3 f (x) = x2 + 4x + 7 Note, h ...
... It’s a simple matter to transform the equation f (x) = (x + 2)2 + 3 into the general form of a quadratic function, f (x) = ax2 + bx + c. We simply use the three-step algorithm to square the binomial; then we combine like terms. f (x) = (x + 2)2 + 3 f (x) = x2 + 4x + 4 + 3 f (x) = x2 + 4x + 7 Note, h ...
modularity of elliptic curves
... curve is modular. Together, Ribet’s and Wiles’s proofs show that the Frey curve does not exist. Thus, the combined efforts of Taniyama, Shimura, Frey, Serre, Ribet, and Wiles, Taylor, and many others resulted in a proof of Fermat’s Last Theorem over three centuries after Fermat’s death. Actually, W ...
... curve is modular. Together, Ribet’s and Wiles’s proofs show that the Frey curve does not exist. Thus, the combined efforts of Taniyama, Shimura, Frey, Serre, Ribet, and Wiles, Taylor, and many others resulted in a proof of Fermat’s Last Theorem over three centuries after Fermat’s death. Actually, W ...
Recurrence Equations
... equivalent constant coefficient linear recurrence of order 1 in much the same way as we transformed (53.3) into such a recurrence. (53.9) is already in the form of (53.17). The recurrence: F (n) = F (n − 1) + F (n − 2), n ≥ 2 defines the Fibonacci numbers when the initial values F (0) = 0 and F (1) ...
... equivalent constant coefficient linear recurrence of order 1 in much the same way as we transformed (53.3) into such a recurrence. (53.9) is already in the form of (53.17). The recurrence: F (n) = F (n − 1) + F (n − 2), n ≥ 2 defines the Fibonacci numbers when the initial values F (0) = 0 and F (1) ...
Ch. 9 :: Workbook/Homework
... Section 9.3 — Addition, Subtraction, and Multiplication of Radical Expressions Section 9.4 — Division of Radical Expressions ...
... Section 9.3 — Addition, Subtraction, and Multiplication of Radical Expressions Section 9.4 — Division of Radical Expressions ...
Equation

In mathematics, an equation is an equality containing one or more variables. Solving the equation consists of determining which values of the variables make the equality true. In this situation, variables are also known as unknowns and the values which satisfy the equality are known as solutions. An equation differs from an identity in that an equation is not necessarily true for all possible values of the variable.There are many types of equations, and they are found in all areas of mathematics; the techniques used to examine them differ according to their type.Algebra studies two main families of equations: polynomial equations and, among them, linear equations. Polynomial equations have the form P(X) = 0, where P is a polynomial. Linear equations have the form a(x) + b = 0, where a is a linear function and b is a vector. To solve them, one uses algorithmic or geometric techniques, coming from linear algebra or mathematical analysis. Changing the domain of a function can change the problem considerably. Algebra also studies Diophantine equations where the coefficients and solutions are integers. The techniques used are different and come from number theory. These equations are difficult in general; one often searches just to find the existence or absence of a solution, and, if they exist, to count the number of solutions.Geometry uses equations to describe geometric figures. The objective is now different, as equations are used to describe geometric properties. In this context, there are two large families of equations, Cartesian equations and parametric equations.Differential equations are equations involving one or more functions and their derivatives. They are solved by finding an expression for the function that does not involve derivatives. Differential equations are used to model real-life processes in areas such as physics, chemistry, biology, and economics.The ""="" symbol was invented by Robert Recorde (1510–1558), who considered that nothing could be more equal than parallel straight lines with the same length.