How to Hash into Elliptic Curves
... case, the discrete logarithm of H(m) with respect to G is known, which makes most protocols insecure. For example, it is easy to see that for Boneh-Franklin identity encryption scheme, the attacker can then decrypt any ciphertext. This remains true if we use H(m) = h1 (m).G1 + h2 (m).G2 or any such ...
... case, the discrete logarithm of H(m) with respect to G is known, which makes most protocols insecure. For example, it is easy to see that for Boneh-Franklin identity encryption scheme, the attacker can then decrypt any ciphertext. This remains true if we use H(m) = h1 (m).G1 + h2 (m).G2 or any such ...
Hypergeometric Solutions of Linear Recurrences with Polynomial
... A sequence a E SK will be called polynomial (respectively rational) a polynomial f (x) E K[x] (respectively a rational function f (x) E K(x)) such that a(n) = f (n) for all large enough n E IN . A non-zero sequence a E SK is a hypergeometric term (or simply hypergeometric) over K if there is a ratio ...
... A sequence a E SK will be called polynomial (respectively rational) a polynomial f (x) E K[x] (respectively a rational function f (x) E K(x)) such that a(n) = f (n) for all large enough n E IN . A non-zero sequence a E SK is a hypergeometric term (or simply hypergeometric) over K if there is a ratio ...
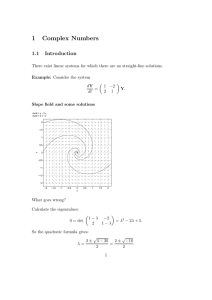
2. Systems of Linear Equations, Matrices
... intersection given by the unique solution we have found. Of course, in general, four planes need not have a point of intersection in common or may have an entire line or plane as their intersection (in the latter case the four equations would each describe the same plane). Systems with solutions are ...
... intersection given by the unique solution we have found. Of course, in general, four planes need not have a point of intersection in common or may have an entire line or plane as their intersection (in the latter case the four equations would each describe the same plane). Systems with solutions are ...
Z/mZ AS A NUMBER SYSTEM As useful as the congruence notation
... (i) If d - b, then the congruence ax ≡ b (mod m) has no solutions. (ii) If d | b, then the congruence ax ≡ b (mod m) has exactly d distinct solutions. We had explained that “distinct solutions” refers to solutions which are distinct modulo m, since x0 ≡ x (mod m), then x is a solution if and only if ...
... (i) If d - b, then the congruence ax ≡ b (mod m) has no solutions. (ii) If d | b, then the congruence ax ≡ b (mod m) has exactly d distinct solutions. We had explained that “distinct solutions” refers to solutions which are distinct modulo m, since x0 ≡ x (mod m), then x is a solution if and only if ...
RICCATI EQUATION AND VOLUME ESTIMATES Contents 1
... 3.1. Example. Suppose that M is complete, and let p ∈ M . Then the distance f = f (q) = d(p, q) from p is a distance function on the open subset W = M \ ({p} ∪ Cp ) of M , where Cp denotes the cut locus of p in M . More generally, if N ⊆ M is a properly embedded submanifold, then the distance f = f ...
... 3.1. Example. Suppose that M is complete, and let p ∈ M . Then the distance f = f (q) = d(p, q) from p is a distance function on the open subset W = M \ ({p} ∪ Cp ) of M , where Cp denotes the cut locus of p in M . More generally, if N ⊆ M is a properly embedded submanifold, then the distance f = f ...
Paper 2. - Siglap Secondary School
... (a) Calculate the value of p. (b) Draw the graph of y = x 2 − 4 x − 5 for − 2 ≤ x ≤ 6 . Use the scale of 2 cm to 1 unit on the horizontal x-axis and 1 cm to 1 unit on the vertical y-axis. (c) Use your graph to find the values of x when y = −1. (d) By drawing a suitable tangent, find the grad ...
... (a) Calculate the value of p. (b) Draw the graph of y = x 2 − 4 x − 5 for − 2 ≤ x ≤ 6 . Use the scale of 2 cm to 1 unit on the horizontal x-axis and 1 cm to 1 unit on the vertical y-axis. (c) Use your graph to find the values of x when y = −1. (d) By drawing a suitable tangent, find the grad ...
Equation

In mathematics, an equation is an equality containing one or more variables. Solving the equation consists of determining which values of the variables make the equality true. In this situation, variables are also known as unknowns and the values which satisfy the equality are known as solutions. An equation differs from an identity in that an equation is not necessarily true for all possible values of the variable.There are many types of equations, and they are found in all areas of mathematics; the techniques used to examine them differ according to their type.Algebra studies two main families of equations: polynomial equations and, among them, linear equations. Polynomial equations have the form P(X) = 0, where P is a polynomial. Linear equations have the form a(x) + b = 0, where a is a linear function and b is a vector. To solve them, one uses algorithmic or geometric techniques, coming from linear algebra or mathematical analysis. Changing the domain of a function can change the problem considerably. Algebra also studies Diophantine equations where the coefficients and solutions are integers. The techniques used are different and come from number theory. These equations are difficult in general; one often searches just to find the existence or absence of a solution, and, if they exist, to count the number of solutions.Geometry uses equations to describe geometric figures. The objective is now different, as equations are used to describe geometric properties. In this context, there are two large families of equations, Cartesian equations and parametric equations.Differential equations are equations involving one or more functions and their derivatives. They are solved by finding an expression for the function that does not involve derivatives. Differential equations are used to model real-life processes in areas such as physics, chemistry, biology, and economics.The ""="" symbol was invented by Robert Recorde (1510–1558), who considered that nothing could be more equal than parallel straight lines with the same length.