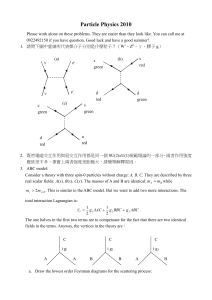
Particle Physics
... θ and initial momentum magnitude p p1 p2 . Only its relations with θ and p are needed. You can drop all the multiplicative constants. Comment: This is the result for a structure-less scattering. Compare it to the answers in 3c, 3d where there is a propagating mediating particle. From the experim ...
... θ and initial momentum magnitude p p1 p2 . Only its relations with θ and p are needed. You can drop all the multiplicative constants. Comment: This is the result for a structure-less scattering. Compare it to the answers in 3c, 3d where there is a propagating mediating particle. From the experim ...
Related Exercises - Cornell Math
... Exercise 3. Try to write out this theorem: “In a quadrilateral, if opposite angles add up to 180◦ , then this quadrilateral is cyclic (i.e. all vertices all lie on one circle)”. Exercise 4. Try to write out this formula: “Straight line AB is tangent to the circle with center O and one point C (i.e. ...
... Exercise 3. Try to write out this theorem: “In a quadrilateral, if opposite angles add up to 180◦ , then this quadrilateral is cyclic (i.e. all vertices all lie on one circle)”. Exercise 4. Try to write out this formula: “Straight line AB is tangent to the circle with center O and one point C (i.e. ...
Uncertainty Principle
... Newtonian physics is viewed as a deterministic system. • Initial positions allow calculation of final states • Knowledge of all past variables implies future knowledge ...
... Newtonian physics is viewed as a deterministic system. • Initial positions allow calculation of final states • Knowledge of all past variables implies future knowledge ...
CONSERVED CURRENTS OF THE MAXWELL EQUATIONS
... deficiency of this formalism is that this Lagrangian is the time component of a vector. Recently this formalism was improved by Sudbery [8] who generalized the previous Lagrangian to a vector, from which he deduced the conserved currents of Lipkin. His Lagrangian for the free Maxwell field was invar ...
... deficiency of this formalism is that this Lagrangian is the time component of a vector. Recently this formalism was improved by Sudbery [8] who generalized the previous Lagrangian to a vector, from which he deduced the conserved currents of Lipkin. His Lagrangian for the free Maxwell field was invar ...
Document
... triangle is greater than the length of the third side. A All of the following must be true: AB+BC>AC BC+AC>AB B AC+AB>BC C *Theorem 5.11 is used to determine whether the three given segments can form a triangle.* ...
... triangle is greater than the length of the third side. A All of the following must be true: AB+BC>AC BC+AC>AB B AC+AB>BC C *Theorem 5.11 is used to determine whether the three given segments can form a triangle.* ...
Lecture 29: Motion in a Central Potential Phy851 Fall 2009
... • Any basis formed from eigenstates of an exactly solvable system plus a weak symmetry breaking perturbation – We can watch the levels evolve as we increase the perturbation strength, and therefore keep track of the quantum numbers ...
... • Any basis formed from eigenstates of an exactly solvable system plus a weak symmetry breaking perturbation – We can watch the levels evolve as we increase the perturbation strength, and therefore keep track of the quantum numbers ...
Are both pairs of opposite sides congruent?
... First use the Distance Formula to show that AB and CD are congruent. AB = ...
... First use the Distance Formula to show that AB and CD are congruent. AB = ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.