Molecular Quantum Chemistry
... There are Nbasis4 two-electron integrals to solve - this is how the method scales with problem size. This can be reduced in actual calculations trough a number of tricks usually down to Nbasis2. ...
... There are Nbasis4 two-electron integrals to solve - this is how the method scales with problem size. This can be reduced in actual calculations trough a number of tricks usually down to Nbasis2. ...
E k
... also Live in another Space: kx-ky-kz Space or Wavevector Space or Momentum Space Remember: Our EE’s Terminologies like V and I want us to see Semiconductors in this additional space as well. ...
... also Live in another Space: kx-ky-kz Space or Wavevector Space or Momentum Space Remember: Our EE’s Terminologies like V and I want us to see Semiconductors in this additional space as well. ...
Adding Fermi-Dirac Statistics to the Drude Model = Sommmerfield
... This is a very simple spin-selective device. Electrons of one angular momentum are favored as they travel past the Schottky barrier due to the external magnetic field and spin filtering in the CoFe. They then fall into the quantum well and recombine with holes. Emission from the quantum well gives a ...
... This is a very simple spin-selective device. Electrons of one angular momentum are favored as they travel past the Schottky barrier due to the external magnetic field and spin filtering in the CoFe. They then fall into the quantum well and recombine with holes. Emission from the quantum well gives a ...
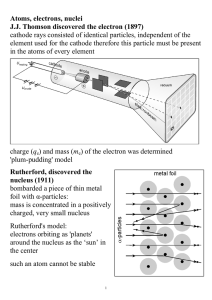
Atoms, electrons, nuclei J.J. Thomson discovered the electron (1897
... Davisson and Germer (1927) used electron beams to induce diffraction through a thin metal foil: interference interference phenomena have been shown with various other particles: duality is a general characteristic of matter Bohr's model (incorrect, but useful) electrons in an atom can only occupy ce ...
... Davisson and Germer (1927) used electron beams to induce diffraction through a thin metal foil: interference interference phenomena have been shown with various other particles: duality is a general characteristic of matter Bohr's model (incorrect, but useful) electrons in an atom can only occupy ce ...
The study of biology can help you better understand
... K ________________________________________________________________ Ca ________________________________________________________________ ...
... K ________________________________________________________________ Ca ________________________________________________________________ ...
2. Fermi Statistics of Electrons and Some Definitions
... The density parameter rs is typically given in bohr units. For metals rs is typically around 2 bohr (remember: this only refers to the valence electrons), and therefore kF is approximately 1 bohr−1 , or 2 Å−1 , respectively. Later, we will often apply Eq. (2.28) - (2.31) because some formulas can be ...
... The density parameter rs is typically given in bohr units. For metals rs is typically around 2 bohr (remember: this only refers to the valence electrons), and therefore kF is approximately 1 bohr−1 , or 2 Å−1 , respectively. Later, we will often apply Eq. (2.28) - (2.31) because some formulas can be ...
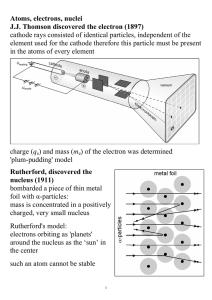
Atoms, electrons, nuclei J.J. Thomson discovered the electron (1897
... Davisson and Germer (1927) used electron beams to induce diffraction through a thin metal foil: interference interference phenomena have been shown with various other particles: duality is a general characteristic of matter Propagation law of free electrons state function ψ(x,t); we can ‘find’ the e ...
... Davisson and Germer (1927) used electron beams to induce diffraction through a thin metal foil: interference interference phenomena have been shown with various other particles: duality is a general characteristic of matter Propagation law of free electrons state function ψ(x,t); we can ‘find’ the e ...
Ch 11 WS Orbitals and Electron Arrangement
... is often thought of as a region of space in which there is a high probability of finding an electron. 8. Circle the letter of the term that is used to label the energy levels of electrons. a. atomic orbitals c. quantum b. quantum mechanical numbers d. principal quantum numbers (n) 9. Principal energ ...
... is often thought of as a region of space in which there is a high probability of finding an electron. 8. Circle the letter of the term that is used to label the energy levels of electrons. a. atomic orbitals c. quantum b. quantum mechanical numbers d. principal quantum numbers (n) 9. Principal energ ...
PES Topography
... Piecewise-linear approximation to density Exact results not known; hence there are several “gradient-corrected” functionals KXC KXC [ ...
... Piecewise-linear approximation to density Exact results not known; hence there are several “gradient-corrected” functionals KXC KXC [ ...
another Exam2
... (c) (5) Now consider the 3-dimensional delta-function potential V (r ) = A ! (r) . Using the first Born approximation again, calculate d! / d" . Determine the constant A which gives the same result as was found in part (b). ...
... (c) (5) Now consider the 3-dimensional delta-function potential V (r ) = A ! (r) . Using the first Born approximation again, calculate d! / d" . Determine the constant A which gives the same result as was found in part (b). ...
Lecture 2
... The Hartree 1-electron equation needs to be solved “self-consistently” to obtain the solutions (i.e., ei and i) for all the electrons! Why? Because the Hartree potential is written in terms of the solutions Thus, Hartree “guessed” the solutions, used these guesses to compute the Hartree potential, ...
... The Hartree 1-electron equation needs to be solved “self-consistently” to obtain the solutions (i.e., ei and i) for all the electrons! Why? Because the Hartree potential is written in terms of the solutions Thus, Hartree “guessed” the solutions, used these guesses to compute the Hartree potential, ...
PHY4605–Introduction to Quantum Mechanics II Spring 1997 Problem Set 4 Jan. 31, 2005
... Problem Set 4 Jan. 31, 2005 Due: Feb. 7, 2005 Reading: Griffiths, Ch. 6 1. Finite extent of proton. The binding energy and ground state of an electron in an H-atom are normally obtained under the assumption that the proton is a fixed point charge, such that the potential is V0 (r) = −e2 /(4π²0 r) al ...
... Problem Set 4 Jan. 31, 2005 Due: Feb. 7, 2005 Reading: Griffiths, Ch. 6 1. Finite extent of proton. The binding energy and ground state of an electron in an H-atom are normally obtained under the assumption that the proton is a fixed point charge, such that the potential is V0 (r) = −e2 /(4π²0 r) al ...
21Sc , 48 22Ti , 50 22Ti , 50
... b) electrons can have either ±½ spins. c) electrons with opposing spins are attracted to each other. ...
... b) electrons can have either ±½ spins. c) electrons with opposing spins are attracted to each other. ...
Aufbau Diagram Directions
... Pauli Exclusion: an atomic orbital may describe at most 2 electrons (each electron will have a different spin) Hund’s Rule: When electrons occupy orbitals of equal energy, one electron enters each orbital until all the orbitas contain one electron, then a second electron is added to each orbital. Ho ...
... Pauli Exclusion: an atomic orbital may describe at most 2 electrons (each electron will have a different spin) Hund’s Rule: When electrons occupy orbitals of equal energy, one electron enters each orbital until all the orbitas contain one electron, then a second electron is added to each orbital. Ho ...
Chapter 2 Part 1 ppt
... Electrons - energy can be measured very accurately, therefore cannot know position (x) with any certainty • Probability of finding an electron at any position (electron density = probability) • Both Schrodinger and Heisenberg proposed ways to treat electrons as waves, Schrodinger’s math was easier ...
... Electrons - energy can be measured very accurately, therefore cannot know position (x) with any certainty • Probability of finding an electron at any position (electron density = probability) • Both Schrodinger and Heisenberg proposed ways to treat electrons as waves, Schrodinger’s math was easier ...
Bohr Model of the Hydrogen Atom
... (c) What is the energy of the ground state, measured in eV (electron volts)? As you likely know from high school physics and/or chemistry courses, the Bohr model predicts the energies of the hydrogen atom incredibly accurately: in fact, not until the introduction of relativistic quantum mechanics wa ...
... (c) What is the energy of the ground state, measured in eV (electron volts)? As you likely know from high school physics and/or chemistry courses, the Bohr model predicts the energies of the hydrogen atom incredibly accurately: in fact, not until the introduction of relativistic quantum mechanics wa ...
Ch1-8 Brown and LeMay Review
... M Ba(OH)2 ? Assume the volumes are additive. Heisenberg Uncertainty Principle Hund’s Rule Wave nature of light Pauli Exclusion Principle Shielding effect A) Can be used to predict that a gaseous carbon atom in its ground state is paramagnetic. B) Explains electron diffraction. C) Indicates that atom ...
... M Ba(OH)2 ? Assume the volumes are additive. Heisenberg Uncertainty Principle Hund’s Rule Wave nature of light Pauli Exclusion Principle Shielding effect A) Can be used to predict that a gaseous carbon atom in its ground state is paramagnetic. B) Explains electron diffraction. C) Indicates that atom ...
Phys 210A — Spring 2016 Problem Set #3: Quantum Statistical
... 1. Relativistic Electron Gas — For an electron whose energy is much larger than the rest energy me c2 , the relation between energy and momentum can be approximated by the extreme relativistic form ε = p · c. This can happen at very high electron density or very high temperature regardless of densit ...
... 1. Relativistic Electron Gas — For an electron whose energy is much larger than the rest energy me c2 , the relation between energy and momentum can be approximated by the extreme relativistic form ε = p · c. This can happen at very high electron density or very high temperature regardless of densit ...
ELECTRONIC PROPERTIES OF GaAs AND HUBBARD
... on the solution of the density functional theory(DFT). It is an integrated suite of computer codes for electronic structure calculations and materials modeling based on DFT,plane waves and pseudopotentials(norm conserving, ultrasoft and projector augmented wave) to represent the electron-ion interac ...
... on the solution of the density functional theory(DFT). It is an integrated suite of computer codes for electronic structure calculations and materials modeling based on DFT,plane waves and pseudopotentials(norm conserving, ultrasoft and projector augmented wave) to represent the electron-ion interac ...
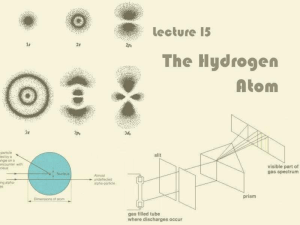
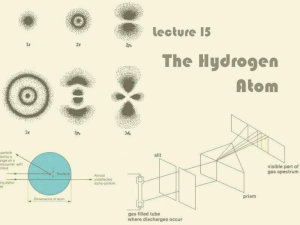
Lecture 15: The Hydrogen Atom
... Balmer’s Formula for Hydrogen Notice there are four bright lines in the hydrogen ...
... Balmer’s Formula for Hydrogen Notice there are four bright lines in the hydrogen ...
Electronic Structure: Density Functional Theory
... Over the years, a vast number of DFT calculations has been reported and only the scantiest of selections can be given here. Results are given for different functionals in order to illustrate the performance of the different levels of approximation. It should be kept in mind, however, that while ther ...
... Over the years, a vast number of DFT calculations has been reported and only the scantiest of selections can be given here. Results are given for different functionals in order to illustrate the performance of the different levels of approximation. It should be kept in mind, however, that while ther ...