Desperately Seeking Superstrings
... Why is the smart money all tied up in strings? Why is so much theoretical capital expended upon the properties of supersymmetric systems of quantum strings propagating in ten-dimensional space-time? The good news is that superstring theory may have the right stuff to explain the “low-energy phenomen ...
... Why is the smart money all tied up in strings? Why is so much theoretical capital expended upon the properties of supersymmetric systems of quantum strings propagating in ten-dimensional space-time? The good news is that superstring theory may have the right stuff to explain the “low-energy phenomen ...
Entanglement and Distinguishability of Quantum States
... fluctuations of the results of the measurements [1]. It is therefore possible to define a statistical distance which is the number of distinguishable states along a certain path in the Hilbert space. We demonstrate that quantum mechanics put an upper bound on the minimal statistical distance among t ...
... fluctuations of the results of the measurements [1]. It is therefore possible to define a statistical distance which is the number of distinguishable states along a certain path in the Hilbert space. We demonstrate that quantum mechanics put an upper bound on the minimal statistical distance among t ...
Foundations of Classical and Quantum Electrodynamics Brochure
... 4.2 The Motion of Charged Particles in Electromagnetic Fields. Transformation of the Electric Field 280 4.2.1 Interaction of Charged Particles with the Electromagnetic Field 280 4.2.2 Equations of Motion of a Relativistic Particle 282 4.2.3 Transformations of Electromagnetic Field Stress 288 4.2.4 D ...
... 4.2 The Motion of Charged Particles in Electromagnetic Fields. Transformation of the Electric Field 280 4.2.1 Interaction of Charged Particles with the Electromagnetic Field 280 4.2.2 Equations of Motion of a Relativistic Particle 282 4.2.3 Transformations of Electromagnetic Field Stress 288 4.2.4 D ...
Nick-Evans
... In the quantum theory we get loops… and use dimensional regulation (d=2-e) to control them… ...
... In the quantum theory we get loops… and use dimensional regulation (d=2-e) to control them… ...
Final
... the superconductor. Assuming ∆ ¿ ²F , find the approximate wavefunctions on the normal and superconducting sides, using continuity. [13 mks] (5) Consider the Hamiltonian for an electron system with a 2-body interaction P P p2 † ap ap + p1 ,p2 ,q qvn a†p1 +q a†p2 −q ap2 ap1 , H = p 2m where v is some ...
... the superconductor. Assuming ∆ ¿ ²F , find the approximate wavefunctions on the normal and superconducting sides, using continuity. [13 mks] (5) Consider the Hamiltonian for an electron system with a 2-body interaction P P p2 † ap ap + p1 ,p2 ,q qvn a†p1 +q a†p2 −q ap2 ap1 , H = p 2m where v is some ...
Workshop on Geometry and Physics 2017 Feb 25
... what he/she is doing. The first 20 minutes of each conference talk should be acceptable to general audience. We also encourage the general participants NOT to attend all the conferences talks, but attend a few talks or part of some talks which are of great interest to themselves. For the technical p ...
... what he/she is doing. The first 20 minutes of each conference talk should be acceptable to general audience. We also encourage the general participants NOT to attend all the conferences talks, but attend a few talks or part of some talks which are of great interest to themselves. For the technical p ...
Chapter41_VG
... turning point at x = L, then it decays exponentially within the classically forbidden region. A similar analysis can be done for x ≤ 0. We can define a parameter η defined as the distance into the classically forbidden region at which the wave function has decreased to e–1 or 0.37 times its value at ...
... turning point at x = L, then it decays exponentially within the classically forbidden region. A similar analysis can be done for x ≤ 0. We can define a parameter η defined as the distance into the classically forbidden region at which the wave function has decreased to e–1 or 0.37 times its value at ...
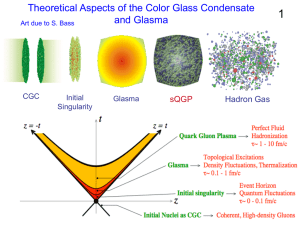
NonequilibriumDynamicsofQuarkGluonPlasma
... invariant results for physical observables. Resulting effective theory for the soft modes contains non-local interactions. ...
... invariant results for physical observables. Resulting effective theory for the soft modes contains non-local interactions. ...
String/M Theory – what is it? Nick Evans
... In the quantum theory we get loops… and use dimensional regulation (d=2-ε) to control them… ...
... In the quantum theory we get loops… and use dimensional regulation (d=2-ε) to control them… ...
Noncommutative space-time and Dirac constraints - Indico
... This anisotropic mechanical system is consistent with the non-relativistic Horava's dispersion relation. Our system corresponds to the Conformal Mechanics for z=2 and is a generalization of this system for arbitrary z. We show that the full Schroedinger algebra constructed from our generators does n ...
... This anisotropic mechanical system is consistent with the non-relativistic Horava's dispersion relation. Our system corresponds to the Conformal Mechanics for z=2 and is a generalization of this system for arbitrary z. We show that the full Schroedinger algebra constructed from our generators does n ...
Appendix
... where Ek2 = k2 + m2 , for Fourier components. We recognize Eq. (13) as the equation for a harmonic oscillator. Thus each Fourier component of the field behaves as an independent harmonic oscillator. In the quantum mechanical treatment of the harmonic oscillator one introduces the creation and annihi ...
... where Ek2 = k2 + m2 , for Fourier components. We recognize Eq. (13) as the equation for a harmonic oscillator. Thus each Fourier component of the field behaves as an independent harmonic oscillator. In the quantum mechanical treatment of the harmonic oscillator one introduces the creation and annihi ...
The energy eigenvalue is E = p2 2m = ¯h2k2 2m = ¯h2 2m (2π L )2
... This is the Airy Equation, and the solution is the Airy Function Ai(z), plotted in Figure 2.1. The Airy Function has a peculiar behavior, oscillatory for negative values of the argument, and decreasing rapidly towards zero for positive values. Of course, this is exactly the behavior we expect for th ...
... This is the Airy Equation, and the solution is the Airy Function Ai(z), plotted in Figure 2.1. The Airy Function has a peculiar behavior, oscillatory for negative values of the argument, and decreasing rapidly towards zero for positive values. Of course, this is exactly the behavior we expect for th ...
UNIT - STUDY GUIDES - SPH 409 QUANTUM MECHANICS II
... 9. Understand the meaning of second quantization for identical particles. SPH 103: Course outline 1. Recall of Basic Ideas of Quantum Theory: Matter waves, de Broglie relations, Heisenberg uncertainty principle, the Schrodinger equation; 2. Approximation Methods: Time – Independent Perturbation Theo ...
... 9. Understand the meaning of second quantization for identical particles. SPH 103: Course outline 1. Recall of Basic Ideas of Quantum Theory: Matter waves, de Broglie relations, Heisenberg uncertainty principle, the Schrodinger equation; 2. Approximation Methods: Time – Independent Perturbation Theo ...
Field theretical approach to gravity
... with Newtonian interaction energy 21 µφ.It follows from here that in Newtonian GmR1 m2 masses m1 , m2 are dressed ones (together with gravitational energy). This is impotent for interaction of heavy compact object (neutron stars) as the essential part of their energy resides in the gravitation field ...
... with Newtonian interaction energy 21 µφ.It follows from here that in Newtonian GmR1 m2 masses m1 , m2 are dressed ones (together with gravitational energy). This is impotent for interaction of heavy compact object (neutron stars) as the essential part of their energy resides in the gravitation field ...