Slide 1
... in degrees. Since there are 360° in a circle, one degree is of a circle. When you use a protractor to measure angles, you are applying the following postulate. ...
... in degrees. Since there are 360° in a circle, one degree is of a circle. When you use a protractor to measure angles, you are applying the following postulate. ...
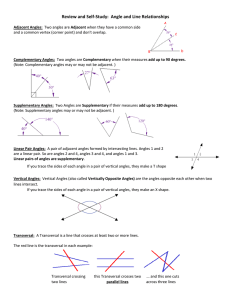
Review and Self-Study: Angle and Line Relationships
... Same Side Interior Angles (also called Consecutive Interior Angles): The pairs of angles on one side of the transversal but inside the two lines are called Same Side Interior Angles. If you trace the sides of each angle in a pair of same side interior angles, they make a C shape or a U shape. ...
... Same Side Interior Angles (also called Consecutive Interior Angles): The pairs of angles on one side of the transversal but inside the two lines are called Same Side Interior Angles. If you trace the sides of each angle in a pair of same side interior angles, they make a C shape or a U shape. ...
4-6
... A and B are on the edges of a ravine. What is AB? One angle pair is congruent, because they are vertical angles. Two pairs of sides are congruent, because their lengths are equal. Therefore the two triangles are congruent by SAS. By CPCTC, the third side pair is congruent, so AB = 18 mi. Holt McDoug ...
... A and B are on the edges of a ravine. What is AB? One angle pair is congruent, because they are vertical angles. Two pairs of sides are congruent, because their lengths are equal. Therefore the two triangles are congruent by SAS. By CPCTC, the third side pair is congruent, so AB = 18 mi. Holt McDoug ...
Ag_mod05_les03 congruent parts of congruent triangles
... A and B are on the edges of a ravine. What is AB? One angle pair is congruent, because they are vertical angles. Two pairs of sides are congruent, because their lengths are equal. Therefore the two triangles are congruent by SAS. By CPCTC, the third side pair is congruent, so AB = 18 mi. Holt McDoug ...
... A and B are on the edges of a ravine. What is AB? One angle pair is congruent, because they are vertical angles. Two pairs of sides are congruent, because their lengths are equal. Therefore the two triangles are congruent by SAS. By CPCTC, the third side pair is congruent, so AB = 18 mi. Holt McDoug ...
4 blog notes congruent triangles
... 3. If not given all needed pieces to prove the triangles congruent, look to see what else you might know about the diagram. 4. Know your definitions! If the given information contains definitions, consider these as "hints" to the solution and be sure to use them. 5. Stay open-minded. There may be mo ...
... 3. If not given all needed pieces to prove the triangles congruent, look to see what else you might know about the diagram. 4. Know your definitions! If the given information contains definitions, consider these as "hints" to the solution and be sure to use them. 5. Stay open-minded. There may be mo ...
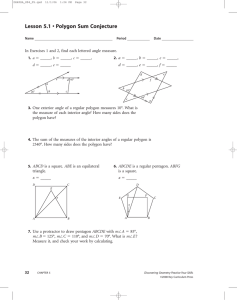
Honors Geometry Name_______________________________
... 21. Which statement is not always true? a) The diagonals of a parallelogram bisect the angles of the parallelogram. b) The diagonals of a rhombus are perpendicular bisectors of each other. c) The diagonals of an isosceles trapezoid are congruent. d) One diagonal of a kite bisects the other diagonal. ...
... 21. Which statement is not always true? a) The diagonals of a parallelogram bisect the angles of the parallelogram. b) The diagonals of a rhombus are perpendicular bisectors of each other. c) The diagonals of an isosceles trapezoid are congruent. d) One diagonal of a kite bisects the other diagonal. ...