* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Geometry EOC Practice Test - Northshore School District
History of trigonometry wikipedia , lookup
Shape of the universe wikipedia , lookup
Analytic geometry wikipedia , lookup
Algebraic geometry wikipedia , lookup
Multilateration wikipedia , lookup
Trigonometric functions wikipedia , lookup
Cartesian coordinate system wikipedia , lookup
Rational trigonometry wikipedia , lookup
Integer triangle wikipedia , lookup
Euler angles wikipedia , lookup
Geometrization conjecture wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Line (geometry) wikipedia , lookup
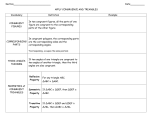
Geometry EOC Practice Exam General Notes This document is not state (OSPI) created or approved. This was developed using resources created by OSPI, the Seattle School District, Mukilteo School District the Bainbridge Island School district and NSD. This is not an exhaustive sampling of EOC Exam test items. Rather it is intended to give students an idea of what their level of understanding is for the Performance Expectations assessed on the state EOC. Purpose of Practice Exam This practice exam has been designed for those students who need to take the Year 2 Retake (EOC Make Up for Geometry) to meet their graduation requirement. This assessment can be used in one of two ways: 1) You can use this as a pretest to see what concepts you need to focus on studying prior to taking the Year 2 Retake. You can go to the companion study guide, “Year 2 Retake Study Guide” to find additional practice problems on those items that you missed on the assessment. 2) You could first review the “Year 2 Retake Study Guide” and then use this practice exam as a post-test. Types of Questions Both this practice exam and the state assessment will have three different types of questions: multiple-choice, completion, and short-answer. For multiple-choice questions, choose the best answer from the four choices given. For short-answer questions, your answers may be graphs, tables, words, or calculations. Resources/Tools Allowed A graphing calculator may be used for all questions.. When you take the state exam, the memory will be cleared. You may also use a straightedge and a compass. The formula page that is on the following two pages will be available during the exam. Organization of the Practice Test The practice exam is organized into the three sections that represent the strands that are assessed for graduation. Section 1: Questions 1 - 4 Logical Argument and Proof Section 2: Questions 5 – 21 Proving and Applying Properties of 2-Dimensional Figures Section 3: Questions 22 – 27 Figures in a Coordinate Plane and Measurement Answers The answers are provided at the end of the document Northshore School District January 2012 Geometry EOC Practice Exam Northshore School District January 2012 Geometry EOC Practice Exam Northshore School District January 2012 Geometry EOC Practice Exam 1. The given statement is a valid geometric proposition If two angles are right angles, then they are congruent. a) Which is the converse of this statement? O A. If two angles are congruent, then they are right angles. O B. If two angles are not congruent, then they are not right angles. O C. If two angles are not right angles, then they are not congruent. O D. If two angles are not right angles, then they could be congruent. b) Is the converse of this statement valid? If it is not valid, then provide a counterexample. 2. Christine knows that if two polygons are congruent, then they must have the same perimeter and area. She concludes that it is also true that if two polygons have the same perimeter and area, then they are congruent. Which pair of polygons can be used as a counterexample to Christine’s conclusion? Northshore School District January 2012 Geometry EOC Practice Exam 3. Given ABC ≅ PRQ, AB ≅ PQ, BC ≅ QR, Elena said that ΔABC ≅ ΔPQR by SAS. Which of the following could be an error in her thinking? o A. The triangles are ≅ by ASA. o B. The triangles are ≅ by SSS. o C. PRQ is not between PQ and RQ. o D. ΔABC is not an isosceles triangle. 4. Which of the following statements is true? o A. A postulate is a proven fact using theorems, definitions, and undefined terms. o B. A theorem is a proven fact using postulates, definitions, and undefined terms. o C. Some defined geometric terms are line, plane, and point. o D. Some undefined geometry terms are angle, ray, and line segment. 5. Find the value of x in the given diagram. x = ________________ 6. Find the value of n. n = ________________ Northshore School District January 2012 Geometry EOC Practice Exam 7. Find the m∠MKL o A. 6 o B. 76 o C. 38 o D. 52 8. ̅̅̅̅ 𝐸𝐷 ̿̿̿̿ 𝐹𝐷 , and ̅̅̅̅ 𝐺𝐷 are the perpendicular bisectors of the sides of ∆ABC. Find BD. BD = ___________________ 9. Identify the angles of ∆XYZ in order from smallest to largest. o A. ∠𝑋, ∠𝑌, ∠𝑍 o B. ∠𝑍, ∠𝑌, ∠𝑋 o C. ∠𝑋, ∠𝑍, ∠𝑌 o D. ∠𝑌, ∠𝑋, ∠𝑍 10. Which theorem or postulate can be used to prove that ∆𝑋𝑌𝑍 ≅ ∆𝑉𝑊𝑍? O A. SSS O B. SAS O C. ASA O D. SSA Northshore School District January 2012 Geometry EOC Practice Exam 11. Complete the proof by writing in the missing statement and reasons. 12. Given: ̅̅̅̅ 𝐴𝐵 ≅ ̅̅̅̅ 𝐸𝐵 and ∠𝐴𝐷𝐵 ≅ ∠𝐸𝐶𝐵 Prove ∆𝐴𝐵𝐷 ≅ ∆𝐸𝐵𝐶 using mathematiacal language and concepts. 13. A lighthouse stands on a hill 80 meters above sea level. The measure of ∠𝑀𝑃𝑄 is 60 degrees and the measure of ∠𝑁𝑃𝑄 is 30 degrees. What is the height of the lighthouse? O A. 80 meters O B. 120 meters O C. 160 meters O D. 240 meters Northshore School District January 2012 Geometry EOC Practice Exam 14. A rectangular prism is shown. The base of the prism is a square. The length of the diagonal from top corner A to opposite bottom corner B is 2 feet. Determine the exact length of the box in inches. Length of Box = __________________ inches 15. Two trees stand on opposite banks of the river, located at points A and B. A surveyor is standing at point C which is 100 feet from point B. He measures angle ACB to be 72 degrees. Determine the length of AB, the width of the river to the nearest hundredth. AB = _____________ figurebelow, belowtois the a right triangle 16. Find the value of a inThe the figure nearest whole number. with measurements given. o A. 10 20 a o B. 11 o C. 14 o D. 16 35° Find the value of a to the nearest whole number. a. 10 b. 11 c. 14 d. 16 Northshore School District January 2012 Geometry EOC Practice Exam 17. In the parallelogram below, m ABC = 70°. Find m ACD. 70 A m ACD. = ______ B 3x-40 2x-5 D 18. Quadrilateral LMNO is a parallelogram. L O C M N Which statement about the parallelogram must be true? O A. ̅̅̅̅ 𝐿𝑁 ≅ ̅̅̅̅̅ 𝑂𝑀 O B. ∆𝐿𝑂𝑁 ≅ ∆𝑁𝑀𝐿 O C. ̅̅̅̅̅ 𝑂𝑀 is the bisector of ∠𝐿𝑂𝑁 O D. ̅̅̅̅ and ̅̅̅̅̅ Diagonals 𝐿𝑁 𝑂𝑀 are perpendicular. 19. Given that PQ = QR = RS = SP, identify the additional information needed to conclude that ABCD is a square. o A. PS || QR o B. PQ || SR o C. PR = QS o D. PQ SR Northshore School District January 2012 Year 2 Retake: EOC Make Up for Geometry Practice Exam 20. Find the value of x in the given isosceles trapezoid. ABCD is an isosceles trapezoid. x = ____________ 30° 25° x Find the value of x 21. The measure of an exterior angle of a regular polygon is 40 degrees. Determine the number of sides the regular polygon has. Number of Sides: __________ 22. ̅̅̅̅. Points R, S and T are collinear. S is the midpoint of 𝑅𝑇 The coordinates of point R are (-4, 5). The coordinates of point S are (-1, 3). Determine the coordinates of point T. Coordinates of point T: _____________ 23. Three vertices of a square have coordinates (3, 1), (4, -4) and (-1, -5). The diagonals of the square intersect at point Q. Determine the coordinates of point Q. You may use the blank grid to help determine the solution. Coordinates of Point Q = ____________ Northshore School District January 2012 Year 2 Retake: EOC Make Up for Geometry Practice Exam 24. The vertices for triangle ABC are A(-6, -4), B(-5, 3), and C(2, 2). What type of triangle is ABC? o A. Scalene right triangle o B. Scalene triangle o C. Equilateral triangle o D. Isosceles right triangle 25. Parallelogram WXYZ is shown on the coordinate grid. Verify that the diagonals the parallelogram bisect each other. 26. A digital camera takes pictures that are 3.2 megabytes in size. If the pictures are stored on a 1-gigabyte card, how many pictures can be taken before the card is full? (There are 1000 megabytes in a gigabyte.) Number of Pictures = _____________ Northshore School District January 2012 Year 2 Retake: EOC Make Up for Geometry Practice Exam 27. A backpack has a volume of 3000 cubic inches. 1 inch = 2.54 centimeters What is the volume of the backpack to the nearest cubic centimeter? o A. 183 cubic centimeters o B. 1,181 cubic centimeters o C. 7,620 cubic centimeters o D. 49, 161 cubic centimeters Northshore School District January 2012 Year 2 Retake: EOC Make Up for Geometry Practice Exam Answers Problem 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. Answer A; not valid any pair of congruent angles that are not 90 degrees would be a counterexample D C B 29 4 C 17 A B 3. ∠𝑅𝑄𝑃 ≅ ∠𝑆𝑄𝑃 4. Reflexive Property of Congruence 5. SAS ̅̅̅̅ ≅ 𝐸𝐵 ̅̅̅̅ and ∠𝐴𝐷𝐵 ≅ ∠𝐸𝐶𝐵 are given pieces of information. ∠𝐴𝐵𝐷 ≅ ∠𝐸𝐵𝐶 because vertical 𝐴𝐵 angles are congruent. ∆𝐴𝐵𝐷 ≅ ∆𝐸𝐵𝐶 by AAS C √414 or 3√46 307.77 ft B 45O B C 95 9 (2, 1) (1, -2) D Diagonals bisect each other since both diagonals have the same midpoint of (1, 1) 312 D Northshore School District January 2012