Precalculus
... Translation of sine and cosine graphs Vertical and horizontal stretching and shrinking of sine and cosine functions Simplifying trigonometric expressions and proving trigonometric identities ...
... Translation of sine and cosine graphs Vertical and horizontal stretching and shrinking of sine and cosine functions Simplifying trigonometric expressions and proving trigonometric identities ...
Teaching about Angles and Triangles for 3rd Grade Students Using
... concept of angles and triangles using origami. The purpose of the research: The research compared two different teaching methods of the following subjects: 1. Angle – it’s definition and marking, identification of a right angle and its comparison to an acute angle, obtuse angel and straight angle. 2 ...
... concept of angles and triangles using origami. The purpose of the research: The research compared two different teaching methods of the following subjects: 1. Angle – it’s definition and marking, identification of a right angle and its comparison to an acute angle, obtuse angel and straight angle. 2 ...
The focus of SECONDARY Mathematics II is on quadratic
... The focus of SECONDARY Mathematics II is on quadratic expressions, equations, and functions; comparing their characteristics and behavior to those of linear and exponential relationships from Secondary Mathematics I as organized into 6 critical areas, or units. Critical Area 1: Students extend the l ...
... The focus of SECONDARY Mathematics II is on quadratic expressions, equations, and functions; comparing their characteristics and behavior to those of linear and exponential relationships from Secondary Mathematics I as organized into 6 critical areas, or units. Critical Area 1: Students extend the l ...
Document
... is greater that the measure of either of it corresponding remote interior angles. • Theorem 5.9 – If one side of a triangle is longer than another side, then the angle opposite the longer side has a greater measure than the angle opposite the shorter side. • Theorem 5.10 – If one angle of a triangle ...
... is greater that the measure of either of it corresponding remote interior angles. • Theorem 5.9 – If one side of a triangle is longer than another side, then the angle opposite the longer side has a greater measure than the angle opposite the shorter side. • Theorem 5.10 – If one angle of a triangle ...
0051_hsm11gmtr_07EM.indd
... 26. ______________________ Is a comparison of two things, sometimes written as a fraction. 27. ______________________ A drawing where all lengths are proportional to their corresponding actual lengths. 28. ______________________ In a proportion, the means are the same. 29. ______________________ Pol ...
... 26. ______________________ Is a comparison of two things, sometimes written as a fraction. 27. ______________________ A drawing where all lengths are proportional to their corresponding actual lengths. 28. ______________________ In a proportion, the means are the same. 29. ______________________ Pol ...
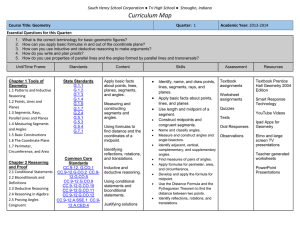
Chapter 1 - South Henry School Corporation
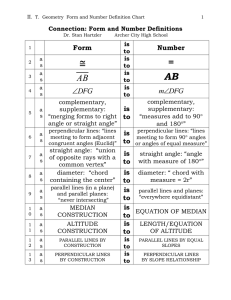
... G.5: Students prove the Pythagorean Theorem and use it to solve problems. They define and apply the trigonometric relations sine, cosine, and tangent. G.5.1: Prove and use the Pythagorean Theorem. G.5.2: State and apply the relationships that exist when the altitude is drawn to the hypotenuse of a r ...
... G.5: Students prove the Pythagorean Theorem and use it to solve problems. They define and apply the trigonometric relations sine, cosine, and tangent. G.5.1: Prove and use the Pythagorean Theorem. G.5.2: State and apply the relationships that exist when the altitude is drawn to the hypotenuse of a r ...
Probability and Geometry Standards
... Geometry and Probability Standards Standards define what students should understand and be able to do. In Geometry and Probability, students will be expected to show proficiency in two standards categories, (1) Standards of Mathematical Content and (2) Standards of Mathematical Practice. Standards o ...
... Geometry and Probability Standards Standards define what students should understand and be able to do. In Geometry and Probability, students will be expected to show proficiency in two standards categories, (1) Standards of Mathematical Content and (2) Standards of Mathematical Practice. Standards o ...