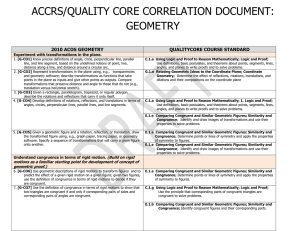
ACCRS/QualityCore-Geometry Correlation - UPDATED
... Congruence; Identify and draw images of transformations and use their properties to solve problems. E.1.g. Comparing Congruent and Similar Geometric Figures; Similarity and Congruence; Determine the geometric mana between two numbers and use it to solve problems (e.g., find the lengths of segments i ...
... Congruence; Identify and draw images of transformations and use their properties to solve problems. E.1.g. Comparing Congruent and Similar Geometric Figures; Similarity and Congruence; Determine the geometric mana between two numbers and use it to solve problems (e.g., find the lengths of segments i ...
UNIT 5 • SIMILARITY, RIGHT TRIANGLE TRIGONOMETRY, AND
... ∠ABE and ∠FCD are not a linear pair. ∠ABC and ∠CBD are a linear pair. They are adjacent angles with non-shared They are not adjacent angles. sides, creating a straight angle. ...
... ∠ABE and ∠FCD are not a linear pair. ∠ABC and ∠CBD are a linear pair. They are adjacent angles with non-shared They are not adjacent angles. sides, creating a straight angle. ...
Midterm Review 2013 (C
... 13) If two lines intersect, they intersect in exactly ____________________________. 14) If two planes intersect, they intersect in exactly ___________________________. 15) Find the circumference and area of the circle with radius of 25m. Use 3.14 for pi. Round to nearest hundredth if necessary. ...
... 13) If two lines intersect, they intersect in exactly ____________________________. 14) If two planes intersect, they intersect in exactly ___________________________. 15) Find the circumference and area of the circle with radius of 25m. Use 3.14 for pi. Round to nearest hundredth if necessary. ...
Geometry
... Proving the Congruent Supplements Theorem Given: Angle 1 and Angle 2 are supplements Angle 3 and Angle 4 are supplements Angle 1 ≅ Angle 4 Prove: Angle 2 ≅ Angle 3 ...
... Proving the Congruent Supplements Theorem Given: Angle 1 and Angle 2 are supplements Angle 3 and Angle 4 are supplements Angle 1 ≅ Angle 4 Prove: Angle 2 ≅ Angle 3 ...
Paper
... Cell phones and other electronic devices may not be brought into the examinations room, not even to be used as calculators. ...
... Cell phones and other electronic devices may not be brought into the examinations room, not even to be used as calculators. ...
Chapter 1 Study Guide
... Congruent angles – angles that have the same measures A point is in the interior of an angle if it is between points that lie on each side of the angle. A point is in the exterior of an angle if it is not on the angle or in its interior. Angle Addition Postulate – If P is in the interior of ...
... Congruent angles – angles that have the same measures A point is in the interior of an angle if it is between points that lie on each side of the angle. A point is in the exterior of an angle if it is not on the angle or in its interior. Angle Addition Postulate – If P is in the interior of ...
Math 460 Euclid`s Propositions 29 - 48 Prop. 29. A straight line
... Prop. 29. A straight line falling on parallel straight lines makes the alternate angles equal to one another, the exterior angle equal to the interior and opposite angle, and the sum of the interior angles on the same side equal to two right angles. Prop. 30. Straight lines parallel to the same stra ...
... Prop. 29. A straight line falling on parallel straight lines makes the alternate angles equal to one another, the exterior angle equal to the interior and opposite angle, and the sum of the interior angles on the same side equal to two right angles. Prop. 30. Straight lines parallel to the same stra ...