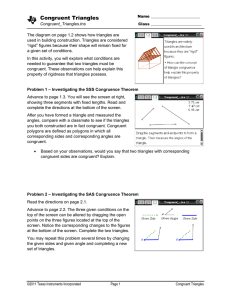
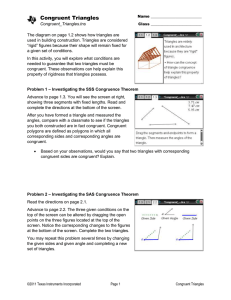
Mathathon Round
... 8. Let r(d) be a function that reverses the digits of the 2-digit integer d. What is the smallest 2-digit positive integer N such that for some 2-digit positive integer n and 2-digit positive integer r(n), N is divisible by n and r(n), but not by 11? Answer: 84 Solution: We want to minimize lcm(r(n) ...
... 8. Let r(d) be a function that reverses the digits of the 2-digit integer d. What is the smallest 2-digit positive integer N such that for some 2-digit positive integer n and 2-digit positive integer r(n), N is divisible by n and r(n), but not by 11? Answer: 84 Solution: We want to minimize lcm(r(n) ...
subject: mathematics - Vijaya Vittala Vidyashala
... II. Fill in the blanks: [1x2] 1. If each exterior angle of a regular polygon is equal to twice its adjacent interior angle, then the number of sides is ___________ 2. The area of a parallelogram is 153.6 cm2 . The base measures 19.2 cm. Then the height of parallelogram is ______________ III. Answer ...
... II. Fill in the blanks: [1x2] 1. If each exterior angle of a regular polygon is equal to twice its adjacent interior angle, then the number of sides is ___________ 2. The area of a parallelogram is 153.6 cm2 . The base measures 19.2 cm. Then the height of parallelogram is ______________ III. Answer ...
Use inductive reasoning to find the next two numbers in each pattern
... Suppose J is between H and K. Use the Segment Addition Postulate to solve for x, then find the length of each segment. HJ = 2x + 5 ...
... Suppose J is between H and K. Use the Segment Addition Postulate to solve for x, then find the length of each segment. HJ = 2x + 5 ...
Weber problem

In geometry, the Weber problem, named after Alfred Weber, is one of the most famous problems in location theory. It requires finding a point in the plane that minimizes the sum of the transportation costs from this point to n destination points, where different destination points are associated with different costs per unit distance.The Weber problem generalizes the geometric median, which assumes transportation costs per unit distance are the same for all destination points, and the problem of computing the Fermat point, the geometric median of three points. For this reason it is sometimes called the Fermat–Weber problem, although the same name has also been used for the unweighted geometric median problem. The Weber problem is in turn generalized by the attraction–repulsion problem, which allows some of the costs to be negative, so that greater distance from some points is better.