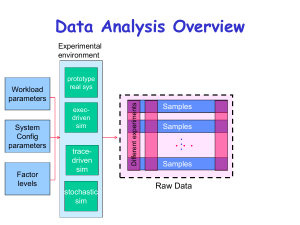
1 Introduction
... Once the term is squared, the equation is complete, and is identically equal to the right hand term above. Thus, in the case of the sample mean, the Jackknife estimate of the standard error reduces ...
... Once the term is squared, the equation is complete, and is identically equal to the right hand term above. Thus, in the case of the sample mean, the Jackknife estimate of the standard error reduces ...
Confidence Intervals for Means
... the same sample. Instead they base the standard deviation of the mean on the historical process standard deviation, estimated from a vast collection of similar parts. In this case, the standard deviation can be treated as “known” and the normal model can be used for the sampling distribution instead ...
... the same sample. Instead they base the standard deviation of the mean on the historical process standard deviation, estimated from a vast collection of similar parts. In this case, the standard deviation can be treated as “known” and the normal model can be used for the sampling distribution instead ...
Applied Statistics
... • If two predictor variables are highly correlated, using both degrades regression • E.g., likely to be a correlation between an executable’s on-disk size and in-core size – So don’t use both as predictors of run time • Which means you need to understand your predictor variables as well as possible ...
... • If two predictor variables are highly correlated, using both degrades regression • E.g., likely to be a correlation between an executable’s on-disk size and in-core size – So don’t use both as predictors of run time • Which means you need to understand your predictor variables as well as possible ...
Estimating the Variance of an Estimate`s Probability Distribution
... b. What is the equation for the best fitting line? c. What are the residuals for each observation? d. Suppose that the quiz scores were different. For example, suppose that Student 1 received a 70 instead of 66. 1) What is the equation for the best fitting line now? 2) What are the residuals for eac ...
... b. What is the equation for the best fitting line? c. What are the residuals for each observation? d. Suppose that the quiz scores were different. For example, suppose that Student 1 received a 70 instead of 66. 1) What is the equation for the best fitting line now? 2) What are the residuals for eac ...
One-Way Analysis of Variance
... The first question that arises concerns which aspects (parameters) of the populations we should compare. We might consider comparing the means, medians, standard deviations, distributional shapes (histograms), or maximum values. We base the comparison parameter on our particular problem. One of the ...
... The first question that arises concerns which aspects (parameters) of the populations we should compare. We might consider comparing the means, medians, standard deviations, distributional shapes (histograms), or maximum values. We base the comparison parameter on our particular problem. One of the ...
Statistics Workshop Introduction to statistics using R Tarik C. Gouhier June 17, 2013
... The Central Limit Theorem The sum or mean of a set of independent random variables drawn from the same statistical population (i.e., identically and independently distributed) will be normally distributed regardless of their parent distribution ...
... The Central Limit Theorem The sum or mean of a set of independent random variables drawn from the same statistical population (i.e., identically and independently distributed) will be normally distributed regardless of their parent distribution ...
Standard Error of the Mean % 95% Confidence Interval
... Standard Error of the Mean *Remember: Standard deviation is a measure of the spread (or average) of the data from the mean. • The sample mean is not necessarily identical to the mean of the entire population. Means will vary with different samples from the same population. • This variability can be ...
... Standard Error of the Mean *Remember: Standard deviation is a measure of the spread (or average) of the data from the mean. • The sample mean is not necessarily identical to the mean of the entire population. Means will vary with different samples from the same population. • This variability can be ...