1 Stat 2300 International – Sample Midterm
... = 1.73. The true standard deviation of the sample mean is approximately 1.73 grams. Let s denote the true standard deviation of the weights. Since samples of size 5 were used, the standard deviation of the sample mean is s/sqrt(5). Thus, s is approximately 1.73*sqrt(5), or 3.87 grams.] 21. Answer: ( ...
... = 1.73. The true standard deviation of the sample mean is approximately 1.73 grams. Let s denote the true standard deviation of the weights. Since samples of size 5 were used, the standard deviation of the sample mean is s/sqrt(5). Thus, s is approximately 1.73*sqrt(5), or 3.87 grams.] 21. Answer: ( ...
Estimating and Finding Confidence Intervals - TI Education
... we took all possible samples of size 10 and calculated the confidence intervals as above, 80 percent of these intervals calculated would contain the correct population mean. In screens 7-17 we generate just ten samples, and seven of the ten contain the true mean. (We did not expect exactly eight of ...
... we took all possible samples of size 10 and calculated the confidence intervals as above, 80 percent of these intervals calculated would contain the correct population mean. In screens 7-17 we generate just ten samples, and seven of the ten contain the true mean. (We did not expect exactly eight of ...
Two Sample Problems
... ▸ Example: Suppose a random samples of ticket prices for concerts by the Rolling Stones was obtained. For comparison purposes another random sample of Coldplay ticket prices was obtained. Note these are not necessarily the same seats or even the same venues. ▸ Question: Are these samples more likely ...
... ▸ Example: Suppose a random samples of ticket prices for concerts by the Rolling Stones was obtained. For comparison purposes another random sample of Coldplay ticket prices was obtained. Note these are not necessarily the same seats or even the same venues. ▸ Question: Are these samples more likely ...
Chapter 5
... goals. In this chapter we shall begin to explore what can be done without an a priori distribution, where our only assumptions involve the family of distributions of the data, f (x|θ). One of the simplest inferential problems to state, is, which of the distributions f (x|θ) is the right one? Or equi ...
... goals. In this chapter we shall begin to explore what can be done without an a priori distribution, where our only assumptions involve the family of distributions of the data, f (x|θ). One of the simplest inferential problems to state, is, which of the distributions f (x|θ) is the right one? Or equi ...
On the Representation and Estimation of Spatial Uncertainty Randall C. Smith*
... tion, the robot must be able to use sensor information to reduce locational uncertainty (in both position and orientation) to a degree sufficient for achieving particular tasks. This problem is complicated in practice because the location of one object relative to another may be known only indirectl ...
... tion, the robot must be able to use sensor information to reduce locational uncertainty (in both position and orientation) to a degree sufficient for achieving particular tasks. This problem is complicated in practice because the location of one object relative to another may be known only indirectl ...
Confidence Interval for a Population Mean
... 9. In order to curtail insider trading, the SEC requested information on the proportion of bank holding companies whose officers directly hold more than 50% of the bank's outstanding stock. Of the 200 banks selected at random, 79 reported that insiders held a majority of their stocks. What is the 9 ...
... 9. In order to curtail insider trading, the SEC requested information on the proportion of bank holding companies whose officers directly hold more than 50% of the bank's outstanding stock. Of the 200 banks selected at random, 79 reported that insiders held a majority of their stocks. What is the 9 ...
TB Ch 09
... ANSWER: $71,000 $13,836 = ($57,164, $84,836). The assumption is that the population is normal or near normal. This is particularly important since the sample size is so small (9). However, the t distribution is rather robust to violations of normality. ...
... ANSWER: $71,000 $13,836 = ($57,164, $84,836). The assumption is that the population is normal or near normal. This is particularly important since the sample size is so small (9). However, the t distribution is rather robust to violations of normality. ...
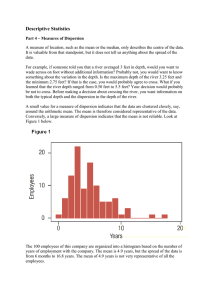
Descriptive Statistics
... The mean deviation has two advantages. First, it uses all the values in the computation whereas the range uses only the highest and the lowest values. Second, it is easy to understand - it is the average amount by which values deviate from the mean. However, its drawback is the use of absolute value ...
... The mean deviation has two advantages. First, it uses all the values in the computation whereas the range uses only the highest and the lowest values. Second, it is easy to understand - it is the average amount by which values deviate from the mean. However, its drawback is the use of absolute value ...