Greek Alphabet Fundamental constants: Useful conversions:
... O ψ = ϕ ; O !"c ψ #$ = c ϕ ; O !" ψ1 + ψ 2 #$ = O ψ1 + O ψ 2 . A vector ϕω is called an eigenvector of an operator O with eigenvalue ω (=complex number) IF O ϕω = ω ϕω . Observables are represented by (Hermitian) operators Ω with only real eigenvalues ωi. Any measurement of the observable must give ...
... O ψ = ϕ ; O !"c ψ #$ = c ϕ ; O !" ψ1 + ψ 2 #$ = O ψ1 + O ψ 2 . A vector ϕω is called an eigenvector of an operator O with eigenvalue ω (=complex number) IF O ϕω = ω ϕω . Observables are represented by (Hermitian) operators Ω with only real eigenvalues ωi. Any measurement of the observable must give ...
From Classical to Quantum Mechanics Chapter 12
... Hydrogen atom consists of a positively charged proton at the center, with a negatively charged electron cloud around it (Rutherford) – The nuclear atom. The electrical attraction between the proton and the electron (centrifugal force) keeps the nucleus and the electrons in the atom ‘together’. Howev ...
... Hydrogen atom consists of a positively charged proton at the center, with a negatively charged electron cloud around it (Rutherford) – The nuclear atom. The electrical attraction between the proton and the electron (centrifugal force) keeps the nucleus and the electrons in the atom ‘together’. Howev ...
Single-Slit and Diffraction Grating
... Single Slit Diffraction, 2 All the waves that originate at the slit are in phase Wave 1 travels farther than wave 3 by an amount equal to the path difference (a/2) sin θ If this path difference is exactly half of a wavelength, the two waves cancel each other and destructive interference results ...
... Single Slit Diffraction, 2 All the waves that originate at the slit are in phase Wave 1 travels farther than wave 3 by an amount equal to the path difference (a/2) sin θ If this path difference is exactly half of a wavelength, the two waves cancel each other and destructive interference results ...
= ∫ ( ) = ∫ ( )
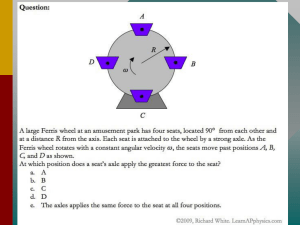
... A woman with mass 50 kg is standing on the rim of a large disk that is rotating at 0.50 rev/s about an axis through its center. The disk has mass 110 kg and radius 4.0 m. Calculate the magnitude of the total angular momentum of the woman-plus-disk system. (Assume that you can treat the woman as a po ...
... A woman with mass 50 kg is standing on the rim of a large disk that is rotating at 0.50 rev/s about an axis through its center. The disk has mass 110 kg and radius 4.0 m. Calculate the magnitude of the total angular momentum of the woman-plus-disk system. (Assume that you can treat the woman as a po ...
January 2004
... Two observers in different inertial frames will need different wave functions to describe the same physical system. To make things simple we will consider how it works in one dimension: The first observer uses coordinates (x, t) and a wave function ψ(x, t) while the second uses (x0 , t) and ψ̂(x0 , ...
... Two observers in different inertial frames will need different wave functions to describe the same physical system. To make things simple we will consider how it works in one dimension: The first observer uses coordinates (x, t) and a wave function ψ(x, t) while the second uses (x0 , t) and ψ̂(x0 , ...
polarization of the allotropic hollow foms of carbon and its use in
... quantum charged particles with total energy E > 0 is offered. The problem is shown to classical quantum-mechanical effect: «a particle in a box» (a Q-particle) in which power conditions are defined by the sizes of a box with the polarizing forces locally operating as a potential barrier or "mirror", ...
... quantum charged particles with total energy E > 0 is offered. The problem is shown to classical quantum-mechanical effect: «a particle in a box» (a Q-particle) in which power conditions are defined by the sizes of a box with the polarizing forces locally operating as a potential barrier or "mirror", ...
Mid Term Test 2012 Answers File
... addition of angular momentum around this axis is the torque, so L moves to L + dt in time dt, i.e. with precessional angular velocity /L = 10/1000 = 10–3 rads–1. c) The potential energy of a body varies with position as U 2x 2 . (i) Give an expression for the force F on the body and sketch F(x) ...
... addition of angular momentum around this axis is the torque, so L moves to L + dt in time dt, i.e. with precessional angular velocity /L = 10/1000 = 10–3 rads–1. c) The potential energy of a body varies with position as U 2x 2 . (i) Give an expression for the force F on the body and sketch F(x) ...
Ch27CTans
... twice the momentum change as photons absorbed by the black side. Therefore, photons striking the white side exert twice the force of photons hitting the black side; the white side should move away from the source. This puzzle is resolved when one realizes there are gas molecules surrounding the padd ...
... twice the momentum change as photons absorbed by the black side. Therefore, photons striking the white side exert twice the force of photons hitting the black side; the white side should move away from the source. This puzzle is resolved when one realizes there are gas molecules surrounding the padd ...
Review Packet
... What is the formula for gravitational potential energy? All forms of energy can be converted into other forms of energy!! What is the Law of Conservation of Energy? Chapter 16 ...
... What is the formula for gravitational potential energy? All forms of energy can be converted into other forms of energy!! What is the Law of Conservation of Energy? Chapter 16 ...
Rotational Motion Practice MC Answers
... An asteroid traveling through space collides with one end of a long, cylindrical satellite as shown above, and sticks to dle satellite. \'\'lllch of the following is erue of dle isolated asteroid-satellite system in tllls collision? a. Kinetic energy K is conserved b. Total Energy E is conserved, bu ...
... An asteroid traveling through space collides with one end of a long, cylindrical satellite as shown above, and sticks to dle satellite. \'\'lllch of the following is erue of dle isolated asteroid-satellite system in tllls collision? a. Kinetic energy K is conserved b. Total Energy E is conserved, bu ...