Electron Configuration - Warren County Public Schools
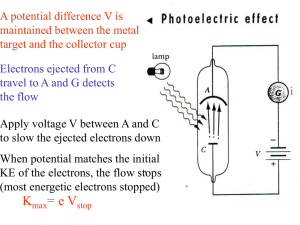
... challenged the wave theory of interaction between light and matter. • The photoelectric effect refers to the emission of electrons from a metal when light shines on it. • The wave theory of light predicted that any frequency of light would supply enough energy to eject an electron. • However, in thi ...
... challenged the wave theory of interaction between light and matter. • The photoelectric effect refers to the emission of electrons from a metal when light shines on it. • The wave theory of light predicted that any frequency of light would supply enough energy to eject an electron. • However, in thi ...
Exercises. 1.1 The power delivered to a photodetector which collects
... to behave as a black-body emitter, what is the temperature of the surface? 1.8 The work function for caesium is 2.14 eV. What is the kinetic energy and the speed of the electrons emitted when the metal is irradiated with light of wavelength (a) 700 nm, (b) 300 nm? 1.9 The photoelectric effect is the ...
... to behave as a black-body emitter, what is the temperature of the surface? 1.8 The work function for caesium is 2.14 eV. What is the kinetic energy and the speed of the electrons emitted when the metal is irradiated with light of wavelength (a) 700 nm, (b) 300 nm? 1.9 The photoelectric effect is the ...
Lecture 29: Motion in a Central Potential Phy851 Fall 2009
... • Any basis formed from eigenstates of an exactly solvable system plus a weak symmetry breaking perturbation – We can watch the levels evolve as we increase the perturbation strength, and therefore keep track of the quantum numbers ...
... • Any basis formed from eigenstates of an exactly solvable system plus a weak symmetry breaking perturbation – We can watch the levels evolve as we increase the perturbation strength, and therefore keep track of the quantum numbers ...
De Broglie waves
... magnitude |ψ|2 evaluated at a particular place at a particular time is proportional to the probability of finding the body there at that time. Probability density. • The probability density |ψ|2 is given by the product of ψ and its complex conjugate ψ*. • The wave function must be single-valued, sup ...
... magnitude |ψ|2 evaluated at a particular place at a particular time is proportional to the probability of finding the body there at that time. Probability density. • The probability density |ψ|2 is given by the product of ψ and its complex conjugate ψ*. • The wave function must be single-valued, sup ...
Problem set 5
... 1. Find the 2 × 2 matrix representing a counter-clockwise rotation (by angle φ about the n̂ direction), of the spin wavefunction of a spin- 12 particle. Express the answer as a linear combination of the identity and Pauli matrices. 2. Show that the exchange operator acting on the Hilbert space of tw ...
... 1. Find the 2 × 2 matrix representing a counter-clockwise rotation (by angle φ about the n̂ direction), of the spin wavefunction of a spin- 12 particle. Express the answer as a linear combination of the identity and Pauli matrices. 2. Show that the exchange operator acting on the Hilbert space of tw ...
Quantum Notes (Chapter 16)(Powerpoint document)
... Any orbital can be identified by a set of three quantum numbers. Any electron can be identified by a s set of four quantum numbers. n, ...
... Any orbital can be identified by a set of three quantum numbers. Any electron can be identified by a s set of four quantum numbers. n, ...
Chapter 4 Arrangement of Electrons in Atoms
... • Explain how the Heisenberg uncertainty principle and the Schrödinger wave equation led to the idea of atomic orbitals. • List the four quantum numbers and describe their significance. • Relate the number of sublevels corresponding to each of an atom’s main energy levels, the number of orbitals per ...
... • Explain how the Heisenberg uncertainty principle and the Schrödinger wave equation led to the idea of atomic orbitals. • List the four quantum numbers and describe their significance. • Relate the number of sublevels corresponding to each of an atom’s main energy levels, the number of orbitals per ...
Lecture XIII_XIV
... The de Broglie wavelength λ for macroscopic particles are negligibly small This effect is extremely important for light particles, like electrons. ...
... The de Broglie wavelength λ for macroscopic particles are negligibly small This effect is extremely important for light particles, like electrons. ...
Lecture Notes, Feb 24, 2016
... looked at de Broglie’s thesis. He work out a single equation, explaining the behavior of particles in terms of de Broglie waves. The lead player in the equation is a quantity called Ψ ( pronounced ”sigh” ) which is called the wave function. • Instead of describing particle by its position and veloci ...
... looked at de Broglie’s thesis. He work out a single equation, explaining the behavior of particles in terms of de Broglie waves. The lead player in the equation is a quantity called Ψ ( pronounced ”sigh” ) which is called the wave function. • Instead of describing particle by its position and veloci ...
2/25/11 QUANTUM MECHANICS II (524) PROBLEM SET 6 (hand in
... 22) (20 points) The hydrogen atom nucleus is a proton with spin I = 1/2. a) In the notation of the preceding problem, what are the possible values of the quantum numbers J and F for a hydrogen atom in the 2p level? b) Use the notation {|n`mi} for the eigenstates of the “simple” hydrogen Hamiltonian ...
... 22) (20 points) The hydrogen atom nucleus is a proton with spin I = 1/2. a) In the notation of the preceding problem, what are the possible values of the quantum numbers J and F for a hydrogen atom in the 2p level? b) Use the notation {|n`mi} for the eigenstates of the “simple” hydrogen Hamiltonian ...
Atomic Spectra Bohr Model Notes
... Developed an equation that treated electrons as waves and described the location of electrons. Helped lay the foundation for modern quantum theory (atomic model). ...
... Developed an equation that treated electrons as waves and described the location of electrons. Helped lay the foundation for modern quantum theory (atomic model). ...
Particle in a box

In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example a ball trapped inside a large box, the particle can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow (on the scale of a few nanometers), quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never ""sit still"". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.The particle in a box model provides one of the very few problems in quantum mechanics which can be solved analytically, without approximations. This means that the observable properties of the particle (such as its energy and position) are related to the mass of the particle and the width of the well by simple mathematical expressions. Due to its simplicity, the model allows insight into quantum effects without the need for complicated mathematics. It is one of the first quantum mechanics problems taught in undergraduate physics courses, and it is commonly used as an approximation for more complicated quantum systems.