PPT
... A roller coaster of mass m starts at rest at height y1 and falls down the path with friction, then back up until it hits height y2 (y1 > y2). An odometer tells us that the total scalar distance traveled is d. Assuming we don’t know anything about the friction or the path, how much work is done by fr ...
... A roller coaster of mass m starts at rest at height y1 and falls down the path with friction, then back up until it hits height y2 (y1 > y2). An odometer tells us that the total scalar distance traveled is d. Assuming we don’t know anything about the friction or the path, how much work is done by fr ...
Chapter 7 Potential Energy and Energy Conservation
... We were able to define potential energy associated with work done by gravitational and elastic forces. All such forces are called conservative forces. Work done by conservative forces: • can always be expressed as difference between initial and final values of a suitably defined potential energy • it ...
... We were able to define potential energy associated with work done by gravitational and elastic forces. All such forces are called conservative forces. Work done by conservative forces: • can always be expressed as difference between initial and final values of a suitably defined potential energy • it ...
Chapter 15
... A special kind of periodic motion occurs in mechanical systems when the force acting on the object is proportional to the position of the object relative to some ...
... A special kind of periodic motion occurs in mechanical systems when the force acting on the object is proportional to the position of the object relative to some ...
5. Universal Laws of Motion
... A compact car and a Mack truck have a head-on collision. Are the following true or false? 1. The force of the car on the truck is equal and opposite to the force of the truck on the car. T 2. The momentum transferred from the truck to the car is equal and opposite to the momentum transferred from th ...
... A compact car and a Mack truck have a head-on collision. Are the following true or false? 1. The force of the car on the truck is equal and opposite to the force of the truck on the car. T 2. The momentum transferred from the truck to the car is equal and opposite to the momentum transferred from th ...
Fundamental of Physics
... 37. (a) We first multiply the vertical axis by the mass, so that it becomes a graph of the applied force. Now, adding the triangular and rectangular “areas” in the graph (for 0 x 4) gives 42 J for the work done. (b) Counting the “areas” under the axis as negative contributions, we find (for 0 ...
... 37. (a) We first multiply the vertical axis by the mass, so that it becomes a graph of the applied force. Now, adding the triangular and rectangular “areas” in the graph (for 0 x 4) gives 42 J for the work done. (b) Counting the “areas” under the axis as negative contributions, we find (for 0 ...
Document
... during which of the 4 seconds does the ball’s speed increase the most? • If you drop a ball from a height of 4.9 m, it will hit the ground 1 s later. If you fire a bullet exactly horizontally from a height of 4.9 m, it will also hit the ground exactly 1 s later. Explain. • If a golf ball and a bowli ...
... during which of the 4 seconds does the ball’s speed increase the most? • If you drop a ball from a height of 4.9 m, it will hit the ground 1 s later. If you fire a bullet exactly horizontally from a height of 4.9 m, it will also hit the ground exactly 1 s later. Explain. • If a golf ball and a bowli ...
GRAVITATION
... Gravitational field: It is the space around a material body in which its gravitational pull can be experienced by other bodies. The strength of gravitational field at a point is the measure of gravitational intensity at that point. The intensity of gravitational field of a body at a point in the f ...
... Gravitational field: It is the space around a material body in which its gravitational pull can be experienced by other bodies. The strength of gravitational field at a point is the measure of gravitational intensity at that point. The intensity of gravitational field of a body at a point in the f ...
Momentum Momentum
... Conservation of Momentum To apply Conservation of Momentum, Take snapshots of a system just before and after an event. By comparing these two snapshots we can learn a lot. We'll explore this more a little later. ...
... Conservation of Momentum To apply Conservation of Momentum, Take snapshots of a system just before and after an event. By comparing these two snapshots we can learn a lot. We'll explore this more a little later. ...
Physics 2010 Summer 2011 REVIEW FOR FINAL EXAM
... The density of ice is 917 kg/m 3 and that of seawater is 1025 kg/m 3. Find the percentage of the iceberg's volume that lies below the surface. The latent heat of vaporization of H 2O at body temperature (37°C) is 2.42 × 10 6 J/kg. To cool the body of a 75.0 kg jogger [average specific heat capacity ...
... The density of ice is 917 kg/m 3 and that of seawater is 1025 kg/m 3. Find the percentage of the iceberg's volume that lies below the surface. The latent heat of vaporization of H 2O at body temperature (37°C) is 2.42 × 10 6 J/kg. To cool the body of a 75.0 kg jogger [average specific heat capacity ...
Name - Deans Community High School
... a. Calculate the loss in potential energy b. What is the kinetic energy of the fish when it hits the water? c. What speed is the fish travelling at on impact with the water? 6. A 20kg box is dropped from a plane flying at 4,000 m a. Calculate the loss in potential energy as it falls ...
... a. Calculate the loss in potential energy b. What is the kinetic energy of the fish when it hits the water? c. What speed is the fish travelling at on impact with the water? 6. A 20kg box is dropped from a plane flying at 4,000 m a. Calculate the loss in potential energy as it falls ...
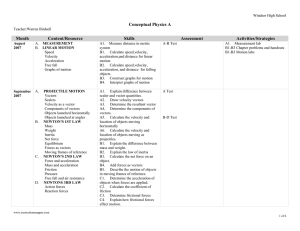
Opportunities for Expository or Explanatory writing
... DISCLAIMER: The activities below are one possible flow. Teachers should feel free to revise the flow and/or use different activities that effectively address the same learning Energy Transfer & Transformation Energy can be transferred (from one place targets. to another). Energy can be transform ...
... DISCLAIMER: The activities below are one possible flow. Teachers should feel free to revise the flow and/or use different activities that effectively address the same learning Energy Transfer & Transformation Energy can be transferred (from one place targets. to another). Energy can be transform ...