LAHS Physics - LAPhysics.com
... 53. If the rope were cut between the block and the pulley, what would be the magnitude of the acceleration of the block down the plane? A) g D) g(tan k sin ) B) g k sin E) g(sin k cos ) C) g k cos 54. A net force F is required to give an object with mass m an acceleration a. If ...
... 53. If the rope were cut between the block and the pulley, what would be the magnitude of the acceleration of the block down the plane? A) g D) g(tan k sin ) B) g k sin E) g(sin k cos ) C) g k cos 54. A net force F is required to give an object with mass m an acceleration a. If ...
Chapter 3: Problems
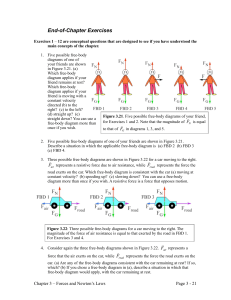
... Figure 3.25: Two situations involving two boxes placed mass of the large box is five times side-by-side on a frictionless surface, for Exercises 18 – 20. larger than that of the small box. You then exert a horizontal force F directed right on the large box. Sketch a free-body diagram for (a) the two ...
... Figure 3.25: Two situations involving two boxes placed mass of the large box is five times side-by-side on a frictionless surface, for Exercises 18 – 20. larger than that of the small box. You then exert a horizontal force F directed right on the large box. Sketch a free-body diagram for (a) the two ...
Sample problem
... Practice Problem: You are driving through town at 12.0 m/s when suddenly a ball rolls out in front of you. You apply the brakes and decelerate at 3.5 m/s2. a) How far do you travel before stopping? ...
... Practice Problem: You are driving through town at 12.0 m/s when suddenly a ball rolls out in front of you. You apply the brakes and decelerate at 3.5 m/s2. a) How far do you travel before stopping? ...
Chapter 7 LINEAR MOMENTUM
... perfectly inelastic collision, the greatest percentage of the kinetic energy is lost. The energy lost by the system in a perfectly inelastic collision is used to do the work required to bring the hammer and nail together. In an elastic collision, this work is available to drive the nail into the woo ...
... perfectly inelastic collision, the greatest percentage of the kinetic energy is lost. The energy lost by the system in a perfectly inelastic collision is used to do the work required to bring the hammer and nail together. In an elastic collision, this work is available to drive the nail into the woo ...
Physics 121C Mechanics
... you to easily solve a problem that involves work and kinetic energy. Solve: 1. Draw the particle first at its initial position and second at its final position. For convenience, the object can be represented as a dot or box. Label the initial and final positions of the object. 2. Put one or more coo ...
... you to easily solve a problem that involves work and kinetic energy. Solve: 1. Draw the particle first at its initial position and second at its final position. For convenience, the object can be represented as a dot or box. Label the initial and final positions of the object. 2. Put one or more coo ...
No Slide Title
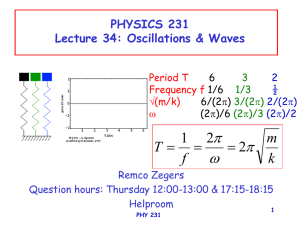
... An anchored fishing boat is going up and down with the waves. It reaches a maximum height every 5 seconds and a person on the boat sees that while reaching a maximum, the previous waves has moves about 40 m away from the boat. What is the speed of the traveling waves? ...
... An anchored fishing boat is going up and down with the waves. It reaches a maximum height every 5 seconds and a person on the boat sees that while reaching a maximum, the previous waves has moves about 40 m away from the boat. What is the speed of the traveling waves? ...
Science-M3-Force-and..
... maintain a force of 2.0 N. Be sure to pull with the scale straight out in front. Practice applying a steady force to the car as it moves. Step 4 Make a data table in your notebook like the one on the next page. Step 5 Find the smallest force needed to pull the car at a slow, constant speed. Do not a ...
... maintain a force of 2.0 N. Be sure to pull with the scale straight out in front. Practice applying a steady force to the car as it moves. Step 4 Make a data table in your notebook like the one on the next page. Step 5 Find the smallest force needed to pull the car at a slow, constant speed. Do not a ...
Document
... To get something moving, you do work on it, the result being kinetic energy. To get objects spinning also takes work, but what is the rotational equivalent of kinetic energy? Problem: in a rotating object, each bit of mass has the same angular speed , but different linear speed v. ...
... To get something moving, you do work on it, the result being kinetic energy. To get objects spinning also takes work, but what is the rotational equivalent of kinetic energy? Problem: in a rotating object, each bit of mass has the same angular speed , but different linear speed v. ...
Lecture 18
... rotational motion. • First, we need to go back and review the nomenclature we use to describe rotational motion. • Motion of an object can be described by translational motion of the CM + rotation of the object around its CM! 95.141, F2010, Lecture 18 ...
... rotational motion. • First, we need to go back and review the nomenclature we use to describe rotational motion. • Motion of an object can be described by translational motion of the CM + rotation of the object around its CM! 95.141, F2010, Lecture 18 ...