ME 242 Chapter 13
... Mathcad does not evaluate cross products symbolically, so the LEFT and RIGHT sides of the above equation are listed below. Equaling the i- and jterms yields two equations for the unknowns wOA and vCOLL ...
... Mathcad does not evaluate cross products symbolically, so the LEFT and RIGHT sides of the above equation are listed below. Equaling the i- and jterms yields two equations for the unknowns wOA and vCOLL ...
Teaching ideas for Topic 2: Mechanics, Core
... is an external force (Mg), but the impulse it produces on the system in an infinitesimal small time t is Mgt and so is negligibly small. It is important to stress that the law of energy conservation (‘energy cannot be created or destroyed but only gets converted from one form to another’) applies ...
... is an external force (Mg), but the impulse it produces on the system in an infinitesimal small time t is Mgt and so is negligibly small. It is important to stress that the law of energy conservation (‘energy cannot be created or destroyed but only gets converted from one form to another’) applies ...
File
... of a resistive force, like friction. The work (or energy) output is the amount of energy the object or system gains as a result of the work being done. It is the work input minus any energy lost as the result of friction. ...
... of a resistive force, like friction. The work (or energy) output is the amount of energy the object or system gains as a result of the work being done. It is the work input minus any energy lost as the result of friction. ...
Kinetic and potential energy
... • Every observable change requires energy. • Energy comes in several different forms (food, electrical, solar, chemical), and can be converted from one form to another. ...
... • Every observable change requires energy. • Energy comes in several different forms (food, electrical, solar, chemical), and can be converted from one form to another. ...
1_4 Elastic_and_in
... because kinetic energy is exchanged between the molecules' translational motion and their internal degrees of freedom with each collision. However, averaged across an entire sample, molecular collisions are elastic. ...
... because kinetic energy is exchanged between the molecules' translational motion and their internal degrees of freedom with each collision. However, averaged across an entire sample, molecular collisions are elastic. ...
The Wizard Test Maker
... (A) The potential energy at A equals the kinetic energy at C. (B) The speed of the pendulum at A equals the speed of the pendulum at B. (C) The potential energy at B equals the potential energy at C. (D) The potential energy at A equals the kinetic energy at B. ...
... (A) The potential energy at A equals the kinetic energy at C. (B) The speed of the pendulum at A equals the speed of the pendulum at B. (C) The potential energy at B equals the potential energy at C. (D) The potential energy at A equals the kinetic energy at B. ...
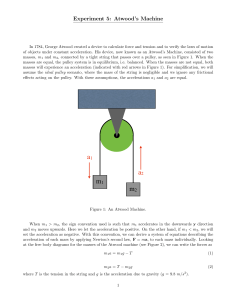
Experiment 5 - Atwood`s Machine
... The object of this lab is to study Newton’s laws of motion and to measure the acceleration due to gravity using the Atwood machine. In this lab you are given various masses, string and a “Photogate with Pulley” sensor that allows you to calculate and graph the position, velocity and the acceleration ...
... The object of this lab is to study Newton’s laws of motion and to measure the acceleration due to gravity using the Atwood machine. In this lab you are given various masses, string and a “Photogate with Pulley” sensor that allows you to calculate and graph the position, velocity and the acceleration ...
Semester Exam Review
... 12. A car drives 40 m west then 115 m south. What is the total displacement and direction of the car? same method as shown in question #10. Displacement = 122 m at 19 degrees S of W ...
... 12. A car drives 40 m west then 115 m south. What is the total displacement and direction of the car? same method as shown in question #10. Displacement = 122 m at 19 degrees S of W ...
Lecture 16 (Feb 29) - West Virginia University
... Two objects (masses: m1, m2) moving at initial velocities v1i and v2i collide. During the time of collision, Δt, object 1 exerts a force F12 on object 2 and object 2 exerts a force F21 on object 1. There are no other external forces! Impulse momentum theorem for m1 and m2: ...
... Two objects (masses: m1, m2) moving at initial velocities v1i and v2i collide. During the time of collision, Δt, object 1 exerts a force F12 on object 2 and object 2 exerts a force F21 on object 1. There are no other external forces! Impulse momentum theorem for m1 and m2: ...
Force and Motion - The Curriculum Project
... object that is moving will continue to move, unless acted on by an outside force? ...
... object that is moving will continue to move, unless acted on by an outside force? ...
Name: ____________________________________ 1. A 20.-newton weight is attached to a spring, causing it to
... A. 30 J B. 60 J C. 300 J D. 600 J 7. An object moving at a constant speed of 25 meters per second possesses 450 joules of kinetic energy. What is the object’s mass? A. 0.72 kg B. 1.4 kg C. 18 kg D. 36 kg 8. An object gains 10. joules of potential energy as it is lifted vertically 2.0 meter ...
... A. 30 J B. 60 J C. 300 J D. 600 J 7. An object moving at a constant speed of 25 meters per second possesses 450 joules of kinetic energy. What is the object’s mass? A. 0.72 kg B. 1.4 kg C. 18 kg D. 36 kg 8. An object gains 10. joules of potential energy as it is lifted vertically 2.0 meter ...
NNHS Introductory Physics: Midyear Review
... know about the friction acting on the object? A. weight A. 10 N of kinetic friction are acting on the object. B. static friction B. 10N of static friction are acting on the object. C. kinetic friction C. Less than 10N of static friction are acting. D. normal force D. Less than 10N of kinetic frictio ...
... know about the friction acting on the object? A. weight A. 10 N of kinetic friction are acting on the object. B. static friction B. 10N of static friction are acting on the object. C. kinetic friction C. Less than 10N of static friction are acting. D. normal force D. Less than 10N of kinetic frictio ...
Chapter 10.3-10.5
... • Why is Newton’s 1st law of motion sometimes called the law of intertia? – Inertia is a measure of an object’s tendency to resist a change in its motion. • Use what you know about inertia to explain why you feel pressed back into the seat of a car when it accelerates? – Because of your inertia, you ...
... • Why is Newton’s 1st law of motion sometimes called the law of intertia? – Inertia is a measure of an object’s tendency to resist a change in its motion. • Use what you know about inertia to explain why you feel pressed back into the seat of a car when it accelerates? – Because of your inertia, you ...
Physical Science Practice Midterm
... you put in. o (W out) can never be greater than (Win) In an ideal machine, Win = Wout o In this system Fe x de = Fr x dr o In most cases, a machine multiplies the force applied to it, Fr is greater than Fe o The machine multiplies your effort but you must move the handle a greater distance. ...
... you put in. o (W out) can never be greater than (Win) In an ideal machine, Win = Wout o In this system Fe x de = Fr x dr o In most cases, a machine multiplies the force applied to it, Fr is greater than Fe o The machine multiplies your effort but you must move the handle a greater distance. ...
1 - Georgetown ISD
... A ball swings freely back and forth in an arc from point I to point IV, as shown above. Point II is the lowest point in the path, III is located 0.5 meter above II, and IV is I meter above II. Air resistance is negligible. 6. If the potential energy is zero at point II, where will the kinetic and po ...
... A ball swings freely back and forth in an arc from point I to point IV, as shown above. Point II is the lowest point in the path, III is located 0.5 meter above II, and IV is I meter above II. Air resistance is negligible. 6. If the potential energy is zero at point II, where will the kinetic and po ...
Physics 2414, Spring 2005 Group Exercise 8, Apr 7, 2005
... Conservation of Energy: The sum of change in kinetic energy ∆K and the change in potential energy ∆U equals the work done by the non-conservative forces. ∆K + ∆U = Σ Wnc . ...
... Conservation of Energy: The sum of change in kinetic energy ∆K and the change in potential energy ∆U equals the work done by the non-conservative forces. ∆K + ∆U = Σ Wnc . ...