Coordination Chemistry III: Electronic Spectra
... with more than one electron, we need to understand in more detail how these electrons interact with each other. • Each conceivable set of individual ml and ms values constitutes a microstate of the configuration. – How many microstates in a d1 configuration? – Examine the carbon atom (p2 configurati ...
... with more than one electron, we need to understand in more detail how these electrons interact with each other. • Each conceivable set of individual ml and ms values constitutes a microstate of the configuration. – How many microstates in a d1 configuration? – Examine the carbon atom (p2 configurati ...
Simple examples of second quantization 4
... with extremely large spin S, but once the spin S becomes small, spins behave as very new kinds of object. Now their spin becomes a quantum variable, subject to its own zero-point motions. Furthermore, the spectrum of excitations becomes discrete or grainy. Quantum spins are notoriously difficult obj ...
... with extremely large spin S, but once the spin S becomes small, spins behave as very new kinds of object. Now their spin becomes a quantum variable, subject to its own zero-point motions. Furthermore, the spectrum of excitations becomes discrete or grainy. Quantum spins are notoriously difficult obj ...
Homework 3: Due in class on Monday, Oct 21st, 2013
... |+i and |−i states, corresponding to the “spin” directed parallel and antiparallel to the field ~h. You should be able to recover the field of the monopole located at the origin of the parameter space, with particular values of the monopole strength (how are those related for |+i and |−i states?) Pr ...
... |+i and |−i states, corresponding to the “spin” directed parallel and antiparallel to the field ~h. You should be able to recover the field of the monopole located at the origin of the parameter space, with particular values of the monopole strength (how are those related for |+i and |−i states?) Pr ...
Document
... Ultracold atomic systems can be used to model condensed-matter physics, providing precise control of system variables often not achievable in real materials. This involves inducing charge-neutral particles to behave as if they were charged particles in a magnetic field. To this end, PFC-supported re ...
... Ultracold atomic systems can be used to model condensed-matter physics, providing precise control of system variables often not achievable in real materials. This involves inducing charge-neutral particles to behave as if they were charged particles in a magnetic field. To this end, PFC-supported re ...
Quantum spin liquids
... theory’. This already contains the basic aspects of quantum fluctuations in ordered systems. The main consequence of long-range order is the presence of low-energy, hydrodynamic fluctuations, as in all systems with long-range order, and this is in essence classical. Specific quantum effects are impo ...
... theory’. This already contains the basic aspects of quantum fluctuations in ordered systems. The main consequence of long-range order is the presence of low-energy, hydrodynamic fluctuations, as in all systems with long-range order, and this is in essence classical. Specific quantum effects are impo ...
Nuclear Spin Ferromagnetic transition in a 2DEG Pascal Simon
... 2D: What about the Mermin-Wagner theorem? The Mermin-Wagner theorem states that there is no finite temperature phase transition in 2D for a Heisenberg model provided that ...
... 2D: What about the Mermin-Wagner theorem? The Mermin-Wagner theorem states that there is no finite temperature phase transition in 2D for a Heisenberg model provided that ...
spin
... We can calculate the renormalised parameters from NRG calculations very accurately. We can generalise the approach to lattice models and calculate the renormalised parameters within DMFT, including an arbitrary magnetic field, and for broken symmetry states. ...
... We can calculate the renormalised parameters from NRG calculations very accurately. We can generalise the approach to lattice models and calculate the renormalised parameters within DMFT, including an arbitrary magnetic field, and for broken symmetry states. ...
ICCP Project 2 - Advanced Monte Carlo Methods
... probability associated with the chosen angle is Pi = wi (θi ) = exp[− βE(θi )]/Zi , where Zi is the local partition function Zi = ∑i wi and is the sum of the weights due to all possible angles for the ith bead. Typically six or so possible angles are allowed as we don’t want to calculate the energy ...
... probability associated with the chosen angle is Pi = wi (θi ) = exp[− βE(θi )]/Zi , where Zi is the local partition function Zi = ∑i wi and is the sum of the weights due to all possible angles for the ith bead. Typically six or so possible angles are allowed as we don’t want to calculate the energy ...
Spin Ensemble
... allowed orientations so that the component along z-axis is either +1/2 or -1/2 ...
... allowed orientations so that the component along z-axis is either +1/2 or -1/2 ...
SMP IOP Hanoi Nov. 18
... Does the partial disorder in Ising systems survive in non-Ising classical and quantum spin systems ? Does the reentrance occur in disorder-free non-Ising spin models ? ...
... Does the partial disorder in Ising systems survive in non-Ising classical and quantum spin systems ? Does the reentrance occur in disorder-free non-Ising spin models ? ...
Modern physics
... History of atomic models: • Thomson discovered electron, invented plum-pudding model • Rutherford observed nuclear scattering, invented orbital atom • Bohr quantized angular momentum, for better H atom model. • Bohr model explained observed H spectra, derived En = E/n2 and phenomenological Rydberg ...
... History of atomic models: • Thomson discovered electron, invented plum-pudding model • Rutherford observed nuclear scattering, invented orbital atom • Bohr quantized angular momentum, for better H atom model. • Bohr model explained observed H spectra, derived En = E/n2 and phenomenological Rydberg ...
Quantum spin chains
... and store it in sparse matrix form, and then find the ground state and first excited state of the Hamiltonian using sparse matrix algorithms. The states of the system can be labelled by an integer s which runs from 0 to 2 L − 1. If we find the binary form of this integer and then change each zero in ...
... and store it in sparse matrix form, and then find the ground state and first excited state of the Hamiltonian using sparse matrix algorithms. The states of the system can be labelled by an integer s which runs from 0 to 2 L − 1. If we find the binary form of this integer and then change each zero in ...
The Wilsonian Revolution in Statistical Mechanics and Quantum
... 2. Landau’s Mean Field Description and Thermodynamics The general theme in the previous section was that systems exhibiting well-separated scales were amenable to different effective descriptions at different scales. Such a result does not immediately seem applicable to gapless systems with degrees of ...
... 2. Landau’s Mean Field Description and Thermodynamics The general theme in the previous section was that systems exhibiting well-separated scales were amenable to different effective descriptions at different scales. Such a result does not immediately seem applicable to gapless systems with degrees of ...
polar molecules in topological order
... coupling strengths that allow them to reach the so-called ‘low-temperature limit’ at experimentally accessible temperatures. The Landau theory of second-order phase transitions associates with every transition a symmetry-breaking mechanism, and with every ordered phase an appearance of a local order ...
... coupling strengths that allow them to reach the so-called ‘low-temperature limit’ at experimentally accessible temperatures. The Landau theory of second-order phase transitions associates with every transition a symmetry-breaking mechanism, and with every ordered phase an appearance of a local order ...
Path integral Monte Carlo study of the interacting quantum double-well... Quantum phase transition and phase diagram
... The mean-field result for Jc, depicted in Fig. 5, shows the same nonmonotonic behavior as our results for Jc from the PIMC simulation and has a maximum at V0 = 1. This behavior of Jc can be understood as follows: In the region V0 Ⰷ 1 the potential has two deep minima separated by a barrier V0 giving ...
... The mean-field result for Jc, depicted in Fig. 5, shows the same nonmonotonic behavior as our results for Jc from the PIMC simulation and has a maximum at V0 = 1. This behavior of Jc can be understood as follows: In the region V0 Ⰷ 1 the potential has two deep minima separated by a barrier V0 giving ...
Quantum phase transitions in atomic gases and
... phase transition at any intermediate value of U/t. (In systems with Galilean invariance and at zero temperature, superfluid density=density of bosons always, independent of the strength of the interactions) ...
... phase transition at any intermediate value of U/t. (In systems with Galilean invariance and at zero temperature, superfluid density=density of bosons always, independent of the strength of the interactions) ...
2 - Physics at Oregon State University
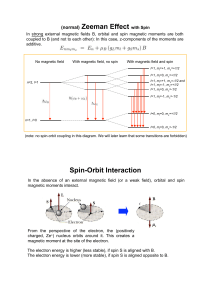
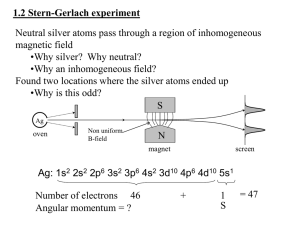
... •How can a neutral atom interact with a magnetic field? •Let’s derive it classically from intro-course principles •What does a simple magnetic dipole look like? •What does the energy look like? •What will the force be and why does the B need to be inhomogeneous? •How do we relate this to angular mom ...
... •How can a neutral atom interact with a magnetic field? •Let’s derive it classically from intro-course principles •What does a simple magnetic dipole look like? •What does the energy look like? •What will the force be and why does the B need to be inhomogeneous? •How do we relate this to angular mom ...
M ph nd nd ph
... Relate the coefficients a,b,c to the parameters of the microscopic BCS Hamiltonian. Show that the coefficient a of the quadratic term changes sign at the BCS transition point, while b and c are positive. 4. Path integral for spin 1 / 2 (optional) In this problem we first introduce a fermionic repres ...
... Relate the coefficients a,b,c to the parameters of the microscopic BCS Hamiltonian. Show that the coefficient a of the quadratic term changes sign at the BCS transition point, while b and c are positive. 4. Path integral for spin 1 / 2 (optional) In this problem we first introduce a fermionic repres ...