atomic and molecular physics using positron traps
... where r0 is the classical electron radius, c is the speed of light, and nm is the number density of atoms or molecules. For large molecules, it is well established that Zeff can greatly exceed the total number of electrons Z in the molecule [5, 8, 12-14]. Consequently, Zeff should be viewed as a nor ...
... where r0 is the classical electron radius, c is the speed of light, and nm is the number density of atoms or molecules. For large molecules, it is well established that Zeff can greatly exceed the total number of electrons Z in the molecule [5, 8, 12-14]. Consequently, Zeff should be viewed as a nor ...
Chapter 4 Classifying Reactions: Chemicals in Balance
... A skeleton equation lists the chemical formula of each reactant on the left, separated by a + sign if more than one reactant is present, followed by →. The chemical formula of each product is listed on the right, separated by a + sign if more than one product is produced. The state of each reactant ...
... A skeleton equation lists the chemical formula of each reactant on the left, separated by a + sign if more than one reactant is present, followed by →. The chemical formula of each product is listed on the right, separated by a + sign if more than one product is produced. The state of each reactant ...
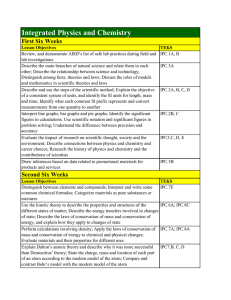
Physical Science Standards
... 2.2 explore matter in terms of specific properties . Performance Indicators State (SPI) and Teacher (TPI): At Level 1, the student is able to SPI distinguish among the phases of matter in terms of volume, shape, and particle arrangement, given illustrations. TPI describe and illustrate the differenc ...
... 2.2 explore matter in terms of specific properties . Performance Indicators State (SPI) and Teacher (TPI): At Level 1, the student is able to SPI distinguish among the phases of matter in terms of volume, shape, and particle arrangement, given illustrations. TPI describe and illustrate the differenc ...
LMM Auger spectra of Cu, Zn, Ga, and Ge, II. Relationship with the L
... in which band bending at the surface and/or nonuniform charging are important contributions to the bandwidth. The values are obtained from a least-squares fit to the L» photoelectron spectra. The line shape of the fit was taken to be the sum of Lorentzian and Gaussian character, while the ratio of t ...
... in which band bending at the surface and/or nonuniform charging are important contributions to the bandwidth. The values are obtained from a least-squares fit to the L» photoelectron spectra. The line shape of the fit was taken to be the sum of Lorentzian and Gaussian character, while the ratio of t ...
Optical Properties of Solids
... of solids is based on a one-electron approximation. an electron is assumed to be acted on by the field of the fixed atomic cores plus an average field arising from the charge distribution of all the other outer-shell electrons. The atomic cores consist of the nuclei and all inner-shell electrons not ...
... of solids is based on a one-electron approximation. an electron is assumed to be acted on by the field of the fixed atomic cores plus an average field arising from the charge distribution of all the other outer-shell electrons. The atomic cores consist of the nuclei and all inner-shell electrons not ...
1 Basic Mean-Field Theory for Bose–Einstein Condensates
... the condensate itself, may range from isotropic forms, to strongly anisotropic ones. In particular, if ωx = ωy ≡ ωr ≈ ωz the trap is isotropic and the BEC is almost spherical, while the cases ωz < ωr or ωr < ωz describe anisotropic traps in which the BEC is, respectively, elongated, “cigar shaped”, ...
... the condensate itself, may range from isotropic forms, to strongly anisotropic ones. In particular, if ωx = ωy ≡ ωr ≈ ωz the trap is isotropic and the BEC is almost spherical, while the cases ωz < ωr or ωr < ωz describe anisotropic traps in which the BEC is, respectively, elongated, “cigar shaped”, ...
Quantum gauge theory simulation with ultracold atoms
... many-body systems: ultracold atomic gases in optical lattices act as genuine quantum simulators. The understanding of gauge theories is essential for the description of the fundamental interactions of our physical world. In particular, gauge theories describe one of the most important class of syste ...
... many-body systems: ultracold atomic gases in optical lattices act as genuine quantum simulators. The understanding of gauge theories is essential for the description of the fundamental interactions of our physical world. In particular, gauge theories describe one of the most important class of syste ...
Nonequilibrium Green`s function approach
... by INSTITUTE OF PHYSICS OF THE CZECH ACADEMY OF SCIENCES on 08/25/14. For personal use only. ...
... by INSTITUTE OF PHYSICS OF THE CZECH ACADEMY OF SCIENCES on 08/25/14. For personal use only. ...
Non-Perturbative Aspects of Nonlinear Sigma Models
... that it is not affected by quantum fluctuations. Explicit calculations [25, 26, 27], however, showed that a more subtle analysis of the renormalization properties is necessary. In order to study this manifestly non-perturbative issue, the FRG should be an adequate tool and first computations in this fr ...
... that it is not affected by quantum fluctuations. Explicit calculations [25, 26, 27], however, showed that a more subtle analysis of the renormalization properties is necessary. In order to study this manifestly non-perturbative issue, the FRG should be an adequate tool and first computations in this fr ...
Polynomial Heisenberg algebras and Painleve
... 2004; Bermudez and Fernández, 2011b]. For some special cases, those can be classified in several solution hierarchies [Bermudez and Fernández, 2011a, 2013a]. In this way, we will find real solutions with real parameters and complex solutions with real and complex parameters for both equations [Ber ...
... 2004; Bermudez and Fernández, 2011b]. For some special cases, those can be classified in several solution hierarchies [Bermudez and Fernández, 2011a, 2013a]. In this way, we will find real solutions with real parameters and complex solutions with real and complex parameters for both equations [Ber ...
A Sequential Molecular Mechanics/Quantum Mechanics Study of the
... defined water molecules. Once a large number of water molecules are considered it is also necessary to account for their numerous configurations. Car-Parrinello molecular dynamics44 coupled with TDDFT provide a fully quantum mechanical description.1,45 The use of a classical description of the solve ...
... defined water molecules. Once a large number of water molecules are considered it is also necessary to account for their numerous configurations. Car-Parrinello molecular dynamics44 coupled with TDDFT provide a fully quantum mechanical description.1,45 The use of a classical description of the solve ...
A semi-classical picture of quantum scattering
... the corresponding positions Xj, for j / 0, the validity of (1.6) for any ^+,^- G L 2 ^), essentially depends on the global shape of the potential V. As an example, it is valid when V(x) < 0 for x ^- 0. In such a case, the result can be extended for general ^+,^_ G ^(R^) by a simple density argument. ...
... the corresponding positions Xj, for j / 0, the validity of (1.6) for any ^+,^- G L 2 ^), essentially depends on the global shape of the potential V. As an example, it is valid when V(x) < 0 for x ^- 0. In such a case, the result can be extended for general ^+,^_ G ^(R^) by a simple density argument. ...























