Syllabus BSCO1 : MATHEMATICS III PARTIAL DIFFERENTIATION
... Introduction, Limit , Partial derivatives , Partial derivatives of Higher orders, Which variable is to be treated as constant, Homogeneous function, Euler’s Theorem on Homogeneous Functions, Introduction, Total Differential Coefficient, Important Deductions, Typical cases, Geometrical Interpretation ...
... Introduction, Limit , Partial derivatives , Partial derivatives of Higher orders, Which variable is to be treated as constant, Homogeneous function, Euler’s Theorem on Homogeneous Functions, Introduction, Total Differential Coefficient, Important Deductions, Typical cases, Geometrical Interpretation ...
Set 9
... 5. Develop the elements equations for a 10-cm rod with boundary conditions of T(0, t) = 40 and T(10, t) = 100 and a uniform heat source of f(x) = 20. Employ four equal-size elements of length = 2.5 cm. Compute the temperature distribution for the entire rod. Ans: x T ...
... 5. Develop the elements equations for a 10-cm rod with boundary conditions of T(0, t) = 40 and T(10, t) = 100 and a uniform heat source of f(x) = 20. Employ four equal-size elements of length = 2.5 cm. Compute the temperature distribution for the entire rod. Ans: x T ...
Solving Linear Inequalities
... Rent-A-Heap car rental agency charges $4 a day plus $0.15 per mile, whereas Clunkers-R-Us rental agency charges $20 a day and $0.05 per mile. How many miles must be driven to make the daily cost of a Rent-A-Heap rental a better deal that a Clunkers-R-Us rental? ...
... Rent-A-Heap car rental agency charges $4 a day plus $0.15 per mile, whereas Clunkers-R-Us rental agency charges $20 a day and $0.05 per mile. How many miles must be driven to make the daily cost of a Rent-A-Heap rental a better deal that a Clunkers-R-Us rental? ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI – 600 034
... 3. Define rank and nullity of a vector space homomorphism T: U V. 4. Give a basis for the vector space F[x] of all polynomials of degree at most n. 5. If V is an inner product space, show that u, v w u, v u, w . 6. Define regular and singular linear transformation. 7. Give an example ...
... 3. Define rank and nullity of a vector space homomorphism T: U V. 4. Give a basis for the vector space F[x] of all polynomials of degree at most n. 5. If V is an inner product space, show that u, v w u, v u, w . 6. Define regular and singular linear transformation. 7. Give an example ...
y - WordPress.com
... Another way to determine whether a function is linear is to look at its equation. A function is linear if it is described by a linear equation. A linear equation is any equation that can be written in the standard form shown below. ...
... Another way to determine whether a function is linear is to look at its equation. A function is linear if it is described by a linear equation. A linear equation is any equation that can be written in the standard form shown below. ...
Algebra II Honors
... Use theorems of polynomial behavior (including but not limited to the Fundamental Theorem of Algebra, Remainder Theorem, the Rational Root Theorem, Descartes' Rule of Signs, and the Conjugate Root Theorem) to find the zeros of a polynomial ...
... Use theorems of polynomial behavior (including but not limited to the Fundamental Theorem of Algebra, Remainder Theorem, the Rational Root Theorem, Descartes' Rule of Signs, and the Conjugate Root Theorem) to find the zeros of a polynomial ...
Gaussian Reflection
... and there is no way to balance O with a whole number, double all the coefficients and try again. (Because O is diatomic as an element) ...
... and there is no way to balance O with a whole number, double all the coefficients and try again. (Because O is diatomic as an element) ...
INTEGER PROGRAMMING WITH 2-VARIABLE EQUATIONS
... have gcd(a, b) = 1 for each equation ax + by = c. Proposition 3. There is an O(N 2 ) time algorithm for solving acyclic connected systems of two variable equations over the integers. Proof. We perform a depth-first search on the graph of the system, starting with any variable x from the system. The ...
... have gcd(a, b) = 1 for each equation ax + by = c. Proposition 3. There is an O(N 2 ) time algorithm for solving acyclic connected systems of two variable equations over the integers. Proof. We perform a depth-first search on the graph of the system, starting with any variable x from the system. The ...
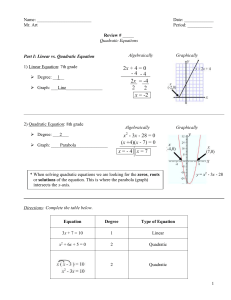
Quadratic Equations - Review - 2012-2013 - Answers
... 1) Standard Form: ax2 + bx + c = 0 (Set equal to zero) x2 term must be positive. Move all terms to the side where + x2 is. If you are given -x2, subtract it over to the other side of the equation to make it positive. 2) Factor completely ...
... 1) Standard Form: ax2 + bx + c = 0 (Set equal to zero) x2 term must be positive. Move all terms to the side where + x2 is. If you are given -x2, subtract it over to the other side of the equation to make it positive. 2) Factor completely ...
Other-Equations
... Quadratic-Form Equations Equations that may be written in the form ax2N + bxN + c = 0 are known as quadratic form equations. For example, the equation 2x8 + 4x4 + 2 = 0 is a quadratic-form equation since the power of the first term, 8, is twice the power of the second term 4. The third term is a re ...
... Quadratic-Form Equations Equations that may be written in the form ax2N + bxN + c = 0 are known as quadratic form equations. For example, the equation 2x8 + 4x4 + 2 = 0 is a quadratic-form equation since the power of the first term, 8, is twice the power of the second term 4. The third term is a re ...
Dr. LM Woodward/Dr. JR Parker - Department of Mathematical
... and give applications; Limit as x of e x / x a ,log x / x a . Leibniz rule. Graph sketching. Graphs of trigonometric and hyperbolic functions. Chain rule. State existence of continuous inverse of monotone continuous function. Differentiation of inverse functions. Inverse trigonometric and hyperb ...
... and give applications; Limit as x of e x / x a ,log x / x a . Leibniz rule. Graph sketching. Graphs of trigonometric and hyperbolic functions. Chain rule. State existence of continuous inverse of monotone continuous function. Differentiation of inverse functions. Inverse trigonometric and hyperb ...