PHYS 1443 – Section 501 Lecture #1
... •All planets move in elliptical orbits with the Sun at one focal point. •The radius vector drawn from the Sun to a planet sweeps out equal area in equal time intervals. (Angular momentum conservation) •The square of the orbital period of any planet is proportional to the cube of the semi-major axis ...
... •All planets move in elliptical orbits with the Sun at one focal point. •The radius vector drawn from the Sun to a planet sweeps out equal area in equal time intervals. (Angular momentum conservation) •The square of the orbital period of any planet is proportional to the cube of the semi-major axis ...
Measurments
... •Newton’s First Law and Inertial Frames Before about 1600, scientists felt that the natural state of matter was the state of rest. Galileo was the first to take a different approach to motion and concluded that it is not the nature of an object to stop once set in motion: rather, it is its nature ...
... •Newton’s First Law and Inertial Frames Before about 1600, scientists felt that the natural state of matter was the state of rest. Galileo was the first to take a different approach to motion and concluded that it is not the nature of an object to stop once set in motion: rather, it is its nature ...
phy201_5 - Personal.psu.edu
... rˆ is the unit vector pointing from the center of motion to the object What causes this acceleration? ...
... rˆ is the unit vector pointing from the center of motion to the object What causes this acceleration? ...
Chp. 7 Outline: Circular Motion and Gravity Lecture Questions: 1
... 1) A cave dweller rotates a pebble in a sling with a radius of .30 m counterclockwise through an arc length of 0.96 m. What is the angular displacement of the pebble? 2) What is the approximate angular speed of a wheel rotating at the rate of 5.0 rev/s? 3) A grinding wheel initially at rest with a r ...
... 1) A cave dweller rotates a pebble in a sling with a radius of .30 m counterclockwise through an arc length of 0.96 m. What is the angular displacement of the pebble? 2) What is the approximate angular speed of a wheel rotating at the rate of 5.0 rev/s? 3) A grinding wheel initially at rest with a r ...
Velocity - SFSU Physics & Astronomy
... Describes speed (How fast is it going?) and direction (Where is it going?) Graphical representation of vectors: length = magnitude; arrowheads = direction ...
... Describes speed (How fast is it going?) and direction (Where is it going?) Graphical representation of vectors: length = magnitude; arrowheads = direction ...
Newton`s Laws of Motion and Vectors
... The motions we observe in our everyday life follow some simple rules. These rules are called Newton’s Laws and can be expressed as follows: First Law: ...
... The motions we observe in our everyday life follow some simple rules. These rules are called Newton’s Laws and can be expressed as follows: First Law: ...
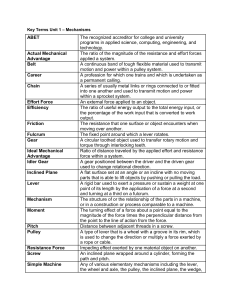
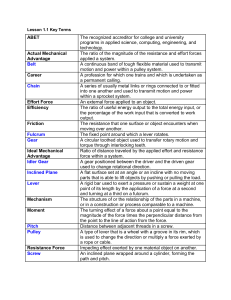
Lesson 1.1 Key Terms ABET The recognized accreditor for college
... The resistance that one surface or object encounters when moving over another. The fixed point around which a lever rotates. A circular toothed object used to transfer rotary motion and torque through interlocking teeth. Ratio of distance traveled by the applied effort and resistance force within a ...
... The resistance that one surface or object encounters when moving over another. The fixed point around which a lever rotates. A circular toothed object used to transfer rotary motion and torque through interlocking teeth. Ratio of distance traveled by the applied effort and resistance force within a ...
9-4,5,6,7
... negligible. Her arms are outstretched, and she is holding a dumbbell in each hand. In this position the total moment of inertia of the rotating system (platform, woman, and dumbbells) is 5.40 kg·m2. By pulling in her arms, she reduces the moment of inertia to 3.80 kg·m2. Find her new angular speed. ...
... negligible. Her arms are outstretched, and she is holding a dumbbell in each hand. In this position the total moment of inertia of the rotating system (platform, woman, and dumbbells) is 5.40 kg·m2. By pulling in her arms, she reduces the moment of inertia to 3.80 kg·m2. Find her new angular speed. ...
Forces and the Laws of Motion Section 3
... •Objects at rest stay at rest and objects in motion stay in motion with the same speed and in the same direction unless acted upon by an unbalanced force. (also called the law of inertia). ...
... •Objects at rest stay at rest and objects in motion stay in motion with the same speed and in the same direction unless acted upon by an unbalanced force. (also called the law of inertia). ...
COURSE EXPECTATIONS COURSE CODE: PHYS
... General and Liberal Science programs, introduces fundamental concepts and physical laws in classical mechanics and their applications in modern science and technology. Topics include: one- and two-dimensional motions; Newton’s three laws of motion and application; work, power, kinetic energy, potent ...
... General and Liberal Science programs, introduces fundamental concepts and physical laws in classical mechanics and their applications in modern science and technology. Topics include: one- and two-dimensional motions; Newton’s three laws of motion and application; work, power, kinetic energy, potent ...
Forces and Motion Learning Outcomes
... 2. Velocity tells us the speed of a moving object and its direction 3. Acceleration is an object’s change in velocity divided by the time it Takes for that change to occur. Forces 4. Gravity is the force that pulls everything around you towards the center of the Earth 5. Friction is a force that act ...
... 2. Velocity tells us the speed of a moving object and its direction 3. Acceleration is an object’s change in velocity divided by the time it Takes for that change to occur. Forces 4. Gravity is the force that pulls everything around you towards the center of the Earth 5. Friction is a force that act ...
Newton`s Second Law
... Use the Weight Comparison Table on pg.78 in the textbook for problems 8-12. 8. If an object’s weight on earth is 75 N, what is its mass? ...
... Use the Weight Comparison Table on pg.78 in the textbook for problems 8-12. 8. If an object’s weight on earth is 75 N, what is its mass? ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.