Chapter 12
... • They need a push or a pull to change their motion… • That push or pull is called a FORCE… • Without a force, their can be no change in motion… ...
... • They need a push or a pull to change their motion… • That push or pull is called a FORCE… • Without a force, their can be no change in motion… ...
Circular Motion - strikerphysics11
... The coordinates x- and yboth change. The speed does not change but the velocity does change (why?) ...
... The coordinates x- and yboth change. The speed does not change but the velocity does change (why?) ...
Newton`s Laws of Motion
... world famous body builder. Chances are that his force will be much greater than yours. Your arms will move in the direction he is pushing with a force that is equal to his force minus your force. It will look like this. ...
... world famous body builder. Chances are that his force will be much greater than yours. Your arms will move in the direction he is pushing with a force that is equal to his force minus your force. It will look like this. ...
Direction of Force and Acceleration
... • Recall that the net force is the combination of all the forces acting on an object. • The net force has a direction: o The net force for forces acting in the same direction is the sum of the forces. o The net force for forces acting in opposite directions is the difference between the forces. ...
... • Recall that the net force is the combination of all the forces acting on an object. • The net force has a direction: o The net force for forces acting in the same direction is the sum of the forces. o The net force for forces acting in opposite directions is the difference between the forces. ...
Document
... A car drives past point x=0 at time t=0 at a constant speed of 50 km/hr. Shortly after it accelerates rapidly to 100 km/hr at t1. It holds this speed until a rabbit runs onto the road at t2 when the car comes to a screeching stop. Which of the curves shown above best represents the car’s i) velocity ...
... A car drives past point x=0 at time t=0 at a constant speed of 50 km/hr. Shortly after it accelerates rapidly to 100 km/hr at t1. It holds this speed until a rabbit runs onto the road at t2 when the car comes to a screeching stop. Which of the curves shown above best represents the car’s i) velocity ...
HOMEWORK – DUE FRIDAY, NOVEMBER 22ND NEWTON`S
... Write “1” if Newton’s first law applies to the statement, “2” if Newton’s seconds law applies to the statement, or “3” if Newton’s third law applies to the statement. 1. Forces occur in action-reaction pairs. 2. When the same amount of force is applied to two objects with different masses, the objec ...
... Write “1” if Newton’s first law applies to the statement, “2” if Newton’s seconds law applies to the statement, or “3” if Newton’s third law applies to the statement. 1. Forces occur in action-reaction pairs. 2. When the same amount of force is applied to two objects with different masses, the objec ...
File
... of a resistive force, like friction. The work (or energy) output is the amount of energy the object or system gains as a result of the work being done. It is the work input minus any energy lost as the result of friction. ...
... of a resistive force, like friction. The work (or energy) output is the amount of energy the object or system gains as a result of the work being done. It is the work input minus any energy lost as the result of friction. ...
Study Guide for Conceptual Physics
... d. A ball is thrown upwards and caught when it comes back down. In the absence of air resistance, the speed of the ball when caught would be? ...
... d. A ball is thrown upwards and caught when it comes back down. In the absence of air resistance, the speed of the ball when caught would be? ...
Newton`s Laws of Motion
... watch it slide to a rest position. The book comes to a rest because of the presence of a force that force being the force of friction which brings the book to a rest position. ...
... watch it slide to a rest position. The book comes to a rest because of the presence of a force that force being the force of friction which brings the book to a rest position. ...
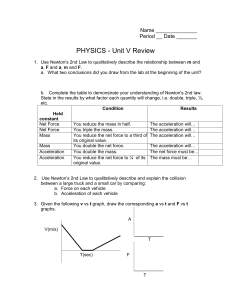
Unit V review
... b. resolving forces into x and y components, then finding the vector sum of the forces. c. analysis of the kinematic behavior of the object. 4. Solve quantitative problems involving forces, mass and acceleration using Newton's 2nd Law. a. Having determined the net force (as in #3), and given the mas ...
... b. resolving forces into x and y components, then finding the vector sum of the forces. c. analysis of the kinematic behavior of the object. 4. Solve quantitative problems involving forces, mass and acceleration using Newton's 2nd Law. a. Having determined the net force (as in #3), and given the mas ...
Early History & Fiction; Orbital Motion
... !" Potential energy of mass, m, depends only on the gravitational force field " !" Kinetic energy of mass, m, depends only on the velocity magnitude measured in an inertial frame of reference " !" Total energy is the sum of the two:" ...
... !" Potential energy of mass, m, depends only on the gravitational force field " !" Kinetic energy of mass, m, depends only on the velocity magnitude measured in an inertial frame of reference " !" Total energy is the sum of the two:" ...
A,C,B,B,C,D,C,D,D,D _____1. A racing car is moving around the
... E. with constant velocity _____2. A ball of mass m is attached to the end of a string of length Q as shown below. The ball is released from rest from position P. where the string is horizontal. It swings through position Q. where the string is vertical, and then to position R. where the string is ag ...
... E. with constant velocity _____2. A ball of mass m is attached to the end of a string of length Q as shown below. The ball is released from rest from position P. where the string is horizontal. It swings through position Q. where the string is vertical, and then to position R. where the string is ag ...
NEWTON’S LAWS OF MOTION
... mass of 0.20 kg and is moving at a velocity of 30 m/s. m = v = p = 3. A truck with a momentum of 85000 kgm/s is moving with a velocity of 50 m/s. Determine its mass. m = v = p = ...
... mass of 0.20 kg and is moving at a velocity of 30 m/s. m = v = p = 3. A truck with a momentum of 85000 kgm/s is moving with a velocity of 50 m/s. Determine its mass. m = v = p = ...
Classical central-force problem
In classical mechanics, the central-force problem is to determine the motion of a particle under the influence of a single central force. A central force is a force that points from the particle directly towards (or directly away from) a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center. In many important cases, the problem can be solved analytically, i.e., in terms of well-studied functions such as trigonometric functions.The solution of this problem is important to classical physics, since many naturally occurring forces are central. Examples include gravity and electromagnetism as described by Newton's law of universal gravitation and Coulomb's law, respectively. The problem is also important because some more complicated problems in classical physics (such as the two-body problem with forces along the line connecting the two bodies) can be reduced to a central-force problem. Finally, the solution to the central-force problem often makes a good initial approximation of the true motion, as in calculating the motion of the planets in the Solar System.