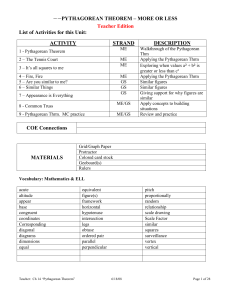
FIELDS ON THE BOTTOM
... We say that a field F lies on the bottom if F contains no field E with 1 < [F : E] < ∞. By definition, each of the prime fields Q and Fp lie on the bottom. By a theorem of Artin, every separably closed field of positive characteristic lies on the bottom (see for example the proof of [Lan93, Cor. 9.3]). I ...
... We say that a field F lies on the bottom if F contains no field E with 1 < [F : E] < ∞. By definition, each of the prime fields Q and Fp lie on the bottom. By a theorem of Artin, every separably closed field of positive characteristic lies on the bottom (see for example the proof of [Lan93, Cor. 9.3]). I ...
Terse Notes on Riemannian Geometry
... Proof. It is easy to check that the unique maximal atlas A0 is given by the set of all charts that are C ∞ -related to all charts in A. Example 2.1. The easiest example of a differentiable manifold is Euclidean space, in which the differentiable structure can be defined by the global chart given by ...
... Proof. It is easy to check that the unique maximal atlas A0 is given by the set of all charts that are C ∞ -related to all charts in A. Example 2.1. The easiest example of a differentiable manifold is Euclidean space, in which the differentiable structure can be defined by the global chart given by ...
FULL TEXT - RS Publication
... collection of pre-open, pre-connected subsets of X. Let A be a pre-open pre-connected subset of X .If AA for all then A( A) is pre-connected. Proof: Suppose that A( A)=BC be a pre - separation of the subset A( A) Since ABC by theorem ( 3.13) ,AB or AC . Without loss of generali ...
... collection of pre-open, pre-connected subsets of X. Let A be a pre-open pre-connected subset of X .If AA for all then A( A) is pre-connected. Proof: Suppose that A( A)=BC be a pre - separation of the subset A( A) Since ABC by theorem ( 3.13) ,AB or AC . Without loss of generali ...
Document
... problems can be easily solved. Even when Maple cannot determine the solution, problem-solving hints can be identified and inferred from the approximate values calculated and solutions to similar problems, as determined by Maple. For this reason, Maple can provide insights into scientific research. I ...
... problems can be easily solved. Even when Maple cannot determine the solution, problem-solving hints can be identified and inferred from the approximate values calculated and solutions to similar problems, as determined by Maple. For this reason, Maple can provide insights into scientific research. I ...
Non-Euclidean Geometry
... Def: Given a point C not on a line AB, the first line through C in either direction that does not meet AB is called a parallel line. Other lines through C which do not meet AB are called nonintersecting lines. The two parallel lines through C are called the right-hand parallel and left-hand parallel ...
... Def: Given a point C not on a line AB, the first line through C in either direction that does not meet AB is called a parallel line. Other lines through C which do not meet AB are called nonintersecting lines. The two parallel lines through C are called the right-hand parallel and left-hand parallel ...
Trigonometry
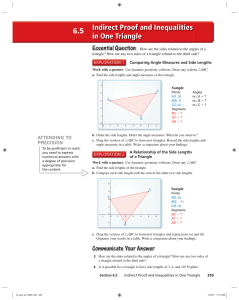
... (Theorem 5.2: Any point equidistant from the endpoints of a segment lies on the perpendicular bisector of the segment.) (Perpendicular bisector (alternative definition using theorem): the locus (set) of all points in a plane equidistant from the endpoints of a given segment.) ...
... (Theorem 5.2: Any point equidistant from the endpoints of a segment lies on the perpendicular bisector of the segment.) (Perpendicular bisector (alternative definition using theorem): the locus (set) of all points in a plane equidistant from the endpoints of a given segment.) ...
Covariance algebra of a partial dynamical system - MATH Mail
... Therefore we have one-to-one correspondence between the commutative unital C ∗ -dynamical systems (A, δ) and pairs (X, α), where X is compact and α is a partial continuous mapping in which the domain is clopen. We shall call (X, α) a partial dynamical system. Usually covariance algebra is another na ...
... Therefore we have one-to-one correspondence between the commutative unital C ∗ -dynamical systems (A, δ) and pairs (X, α), where X is compact and α is a partial continuous mapping in which the domain is clopen. We shall call (X, α) a partial dynamical system. Usually covariance algebra is another na ...
Chapter 3 Foundations of Geometry 2
... Corrolary 3.40 (HA Theorem) If two right triangles have the hypotenuse and acute angle of one congruent, respectively, to the hypotenuse and acute angle of the other, the triangles are congruent. Corrolary 3.41 (LA Theorem) If under some correspondence between their vertices, two right triangles hav ...
... Corrolary 3.40 (HA Theorem) If two right triangles have the hypotenuse and acute angle of one congruent, respectively, to the hypotenuse and acute angle of the other, the triangles are congruent. Corrolary 3.41 (LA Theorem) If under some correspondence between their vertices, two right triangles hav ...
projective limits - University of California, Berkeley
... THEOREM 2.1. If the Bochner condition holds, and if every simple subpresheaf has a limit (that is, the limit measure is a-additive), then i is a-additive. It should be remarked that it is enough to assume the existence of the limit for a sufficiently rich family of simple subpresheaves. 2.3. Since t ...
... THEOREM 2.1. If the Bochner condition holds, and if every simple subpresheaf has a limit (that is, the limit measure is a-additive), then i is a-additive. It should be remarked that it is enough to assume the existence of the limit for a sufficiently rich family of simple subpresheaves. 2.3. Since t ...
Brouwer fixed-point theorem

Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f mapping a compact convex set into itself there is a point x0 such that f(x0) = x0. The simplest forms of Brouwer's theorem are for continuous functions f from a closed interval I in the real numbers to itself or from a closed disk D to itself. A more general form than the latter is for continuous functions from a convex compact subset K of Euclidean space to itself.Among hundreds of fixed-point theorems, Brouwer's is particularly well known, due in part to its use across numerous fields of mathematics.In its original field, this result is one of the key theorems characterizing the topology of Euclidean spaces, along with the Jordan curve theorem, the hairy ball theorem and the Borsuk–Ulam theorem.This gives it a place among the fundamental theorems of topology. The theorem is also used for proving deep results about differential equations and is covered in most introductory courses on differential geometry.It appears in unlikely fields such as game theory. In economics, Brouwer's fixed-point theorem and its extension, the Kakutani fixed-point theorem, play a central role in the proof of existence of general equilibrium in market economies as developed in the 1950s by economics Nobel prize winners Kenneth Arrow and Gérard Debreu.The theorem was first studied in view of work on differential equations by the French mathematicians around Poincaré and Picard.Proving results such as the Poincaré–Bendixson theorem requires the use of topological methods.This work at the end of the 19th century opened into several successive versions of the theorem. The general case was first proved in 1910 by Jacques Hadamard and by Luitzen Egbertus Jan Brouwer.