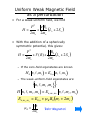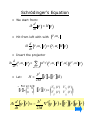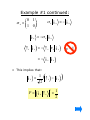Download Lecture 33: Quantum Mechanical Spin

Lecture 33:
Quantum Mechanical Spin
Phy851 Fall 2009
Intrinsic Spin
• Empirically, we have found that most
particles have an additional internal
degree of freedom, called ‘spin’
• The Stern-Gerlach experiment (1922):
• Each type of particle has a discrete
number of internal states:
– 2 states --> spin _
– 3 states --> spin 1
– Etc….
Interpretation
• It is best to think of spin as just an
additional quantum number needed to
specify the state of a particle.
– Within the Dirac formalism, this is
relatively simple and requires no new
physical concepts
• The physical meaning of spin is not wellunderstood
• Fro Dirac eq. we find that for QM to be
Lorentz invariant requires particles to
have both anti-particles and spin.
• The ‘spin’ of a particle is a form of
angular momentum
Spin Operators
• Spin is described by a vector operator:
r
r
r
r
S = S x ex + S y e y + S z ez
• The components satisfy angular
momentum commutation relations:
[ S x , S y ] = ihS z
[ S y , S z ] = ihS x
[ S z , S x ] = ihS y
• This means simultaneous eigenstates of
S2 and Sz exist:
S 2 = S x2 + S y2 + S z2
S 2 s, ms = h 2 s ( s + 1) s, ms
S z s, ms = hm s, ms
Allowed quantum numbers
• For any set of 3 operators satisfying the
angular momentum algebra, the allowed
values of the quantum numbers are:
j ∈ {0, 12 ,1, 32 , K}
m j ∈ {− j ,− j + 1, K , j}
• For orbital angular momentum, the
allowed values were further restricted to
only integer values by the requirement
that the wavefunction be single-valued
• For spin, the quantum number, s, can
only take on one value
– The value depends on the type of particle
– S=0: Higgs
– s=1/2: Electrons, positrons, protons,
neutrons, muons,neutrinos, quarks,…
– s=1: Photons, W, Z, Gluon
– s=2: graviton
ms ∈ {− s,− s + 1, K , s}
Complete single particle basis
• A set of 5 commuting operators which
describe the independent observables of
a single particle are:
r 2
R, S , S z
– Or equivalently:
2
2
R , L , Lz , S , S z
• Some possible basis choices:
r
{r , s, ms
r
{p, s, ms
}
}
{r , l, m , s, m }
{n, l, m , s, m }
l
s
l
s
• When dealing with a single-particle, it is
permissible to drop the s quantum
number
Intrinsic Magnetic Dipole
Moment
• Due to spin, an electron has an intrinsic
magnetic dipole moment:
ge e r
r
µe = −
S
2me
– ge is the electron g-factor
– For an electron, we have:
g e = 2.0023193043622 ± 0.0000000000015
– The is the most precisely measured
physical quantity
• For most purposes, we can take ge≈ 2,
so that
e r
r
µe = − S
me
• For any charged particle we have:
r gq r
µ=
S
2M
Each particle
has a different
g-factor
Hamiltonian for an electron in
a magnetic field
• Because the electron is a point-particle,
the dipole-approximation is always valid
for the spin degree of freedom
• Any `kinetic’ energy associated with S2
is absorbed into the rest mass
• To obtain the full Hamiltonian of an
electron, we must add a single term:
e r r r
H →H+
S ⋅ B(R)
me
r r 2
r
e r r r
1 r
H=
P + e A( R) − e Ö ( R) +
S ⋅ B( R)
2me
me
[
]
Uniform Weak Magnetic Field
as a perturbation
• For a weak uniform field, we find
e B0
P2
(Lz + 2S z )
H=
+
2me 2me
• With the addition of a spherically
symmetric potential, this gives:
e B0
P2
(Lz + 2S z )
H=
+ V ( R) +
2me
2me
– If the zero-field eigenstates are known
H 0 n, l, ml = E0,n n, l, ml
– The weak-uniform-field eigenstates are:
{n, l, m , m }
l
s
H n, l, ml , ms = En ,ml ,ms n, l, ml , ms
En ,ml ,ms = E0,n + µ B B0 (ml + 2ms )
µB =
eh
2me
‘Bohr Magneton’
Wavefunctions
• In Dirac notation, all spin does is add
two extra quantum numbers
• The separate concept of a ‘spinor’ is
unnecessary
• Coordinate basis:
r
{r , s, ms
r 2
R, S , S z
– Eigenstate of
}
• Projector:
I=
s
∑
r
r
∫ d r r , s , ms r , s , ms
3
ms = − s V
• Wavefunction:
r
r
ψ ms (r ):= r , s, ms ψ
Spinor Notation:
r
r
ψ ms (r ):= r , s, ms ψ
• We think of them as components of a
length 2s+1 vector, where each
component is a wavefunction
• Example: s=1/2
r
ψ ↑ (r ):=
r
ψ ↓ (r ):=
r 1
r , s, 2 ψ
r
r , s,− 12 ψ
• Spinor wavefunction definition:
r
r
r ψ ↑ (r )  ψ 12 (r ) 
[ψ ](r ):=  r  =  r 
ψ ↓ (r ) ψ − 12 (r )
Note that
descending order
is unusual
• If external and internal motions are not
entangled, we can factorize the spinor
wavefunction:
r  c↑  r
[ψ ](r ):=  ψ (r )
 c↓ 
 c↑ 
 
 c↓ 
Is then a
pure spinor
Schrödinger's Equation
• We start from:
d
ih ψ = H ψ
dt
• Hit from left with with
r
r , ms
r
d r
ih
r , ms ψ = r , ms H ψ
dt
• Insert the projector
s
r
r
r
d r
3
′
′
′
ih
r , ms ψ = ∑ ∫ d r r , ms H r , ms r ′, m′ ψ
dt
m′s = − s V
r
P2
[[I ]]+ [[V ]]( R)
H=
2M
• Let:
– For s=1/2:
1 0

0 1
[[I ]]= 
r
r
r V↑↑ (r ) V↑↓ (r ) 
[[V ]](r ) =  r
r 
V↓↑ (r ) V↓↓ (r ) 
2
r
r
r
r
d
h
2
ih [ψ ](r ) = −
∇ [ψ ](r )+ [[V ]](r )[ψ ](r )
dt
2M
Example: Electron in a Uniform
Field
r
r
r
r
d
h2 2
ih [ψ ](r ) = −
∇ [ψ ](r )+ [[V ]](r )[ψ ](r )
dt
2M
r
r
r
2
(
)
(
)
(
)
ψ
r
ψ
r
ψ
r
1
0









d
h
∂
↑
↑
↑
2







ih 
∇ − iµ B B0 
r  = −
r  + µ B B0 
r 


dt ψ ↓ (r )  2me
∂φ ψ ↓ (r )
 0 − 1ψ ↓ (r )
• This is just a representation of two
separate equations:
r  h2 2
r
r
d
∂ 
ih ψ ↑ (r ) = −
∇ − iµ B B0 ψ ↑ (r )+ µ B B0ψ ↑ (r )
dt
∂φ 
 2me
r  h2 2
r
r
d
∂ 
ih ψ ↓ (r ) = −
∇ − iµ B B0 ψ ↓ (r )− µ B B0ψ ↓ (r )
dt
∂φ 
 2me
• We would have arrived at these same
equations using Dirac notation, without
ever mentioning ‘Spinors’
Pauli Matrices
r
r
r
2
(
)
(
)
(
ψ
r
ψ
r
ψ
r
1
0

 ↑ )
d  ↑   h
∂  ↑ 
2

ih 
∇ − iµ B B0 
r  = −
r  + µ B B0 
r 
(
)
(
)
(
ψ
r
ψ
r
ψ
r
dt  ↓   2me
∂φ  ↓ 
 0 − 1 ↓ )
• Here we see that we have recovered one
of the Pauli Matrices:
1 0 

σ z = 
 0 − 1
• The other Pauli matrices are:
0 1

σ x = 
1 0
0 − i

σ y = 
i 0 
• Then in the basis of eigenstates of
we have:
r
Sz
h r
S= σ
2


r  h2 2
r
d
∂


ih [ψ ](r ) =  −
∇ + µ B B0  − i
+ σ z  [ψ ](r )
dt
 ∂φ

 2M
• If we only care about spin dynamics:
e r r
d
i [c ]=
σ ⋅ B[c ]
dt
2me
Two particles with spin
• How do we treat a system of two
particles with masses M1 and M2, charges
q1 and q2, and spins s1 and s2?
– Basis:
r
r
r1 , s1 , ms1 ; r2 , s2 , ms 2
– Wavefunction:
r r
r
r
ψ s1 ,ms1 , s2 ,ms 2 (r1 , r2 ) := r1 , s1 , ms1 ; r2 , s2 , ms 2 ψ
– Hamiltonian w/out motional degrees of
freedom:
q1 r r r
q2 r r r
H =−
S1 ⋅ B( R1 ) −
S 2 ⋅ B( R2 )
M1
M2
– Hamiltonian w/ motional degrees of
freedom:
r r
r
1 r
q1 r r r
H=
P1 − q1 A( R1 ) + q1Φ ( R1 ) −
S1 ⋅ B( R1 )
2M 1
M1
r r
r
1 r
q2 r r r
P2 − q2 A( R2 ) + q2 Φ ( R2 ) −
S 2 ⋅ B( R2 )
2M 2
M2
(
)
(
)
Example #1
• A spin _ particle is in the ↑ state with
respect to the z-axis. What is the
probability of finding it in the ↓-state
with respect to the x-axis?
• Let:
ψ = ↑z
{↑
,↓
}
z
z
• In the basis,
the operator
for the x-component of spin is:
0 1

σ x = 
1 0
• By symmetry, σx must have eigenvalues
+1 and -1
• The eigenvector corresponding to -1 is
defined by:
σ x ↓x = − ↓x
Example #1 continued:
0 1

σ x = 
1 0
σ x ↓x = − ↓x
↓ x = −σ x ↓ x
= −1
↑z ↓x = − ↑z σ x ↓x
= − ↓z ↓x
• This implies that:
↓x
1
=
↑z − ↓z
2
(
P = ↓x ↑z
2
1
=
2
)
Example #2
• Two identical spin-1/2 particles are placed
in a uniform magnetic field. Ignoring
motional degrees of freedom, what are the
energy-levels and degeneracies of the
system?
• States:
{↑↑ , ↑↓ , ↓↑ , ↓↓ }
– Z-axis chosen along B-field
• Hamiltonian:
gqB0
(S1z + S 2 z )
H =−
2M
• Basis states are already eigenstates:
hgqB0
H ↑↑ = −
↑↑
2M
H ↑↓ = H ↓↑ = 0
hgqB0
E1 = −
; d1 = 1
2M
hgqB0
H ↓↓ =
↓↓
2M
hgqB0
E3 =
; d3 = 1
2M
E2 = 0; d 2 = 2