* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Weizmann Institute of Science
History of optics wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Relational approach to quantum physics wikipedia , lookup
Circular dichroism wikipedia , lookup
Nuclear physics wikipedia , lookup
Quantum potential wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Time in physics wikipedia , lookup
Quantum entanglement wikipedia , lookup
History of quantum field theory wikipedia , lookup
Hydrogen atom wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
A Brief History of Time wikipedia , lookup
Old quantum theory wikipedia , lookup
EPR paradox wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Bell's theorem wikipedia , lookup
Spin (physics) wikipedia , lookup
Introduction to quantum mechanics wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
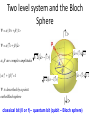
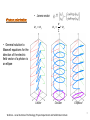
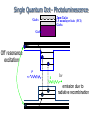
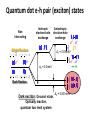
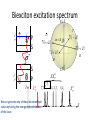
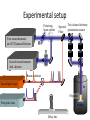
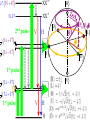
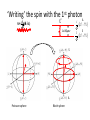
March 29, 2011, Aussois, France David Gershoni The Physics Department, Technion-Israel Institute of Technology, Haifa, 32000, Israel and Joint Quantum Institute, NIST and University of Maryland, USA Technion – Israel Institute of Technology Physics Department and Solid State Institute Motivation Coherent control of anchored qubits – spins of carriers. Coherent control of flying qubits – polarization of photons. Semiconductor Quantum dots provide a unique stage for controlling the interactions between both type of qubits, and they are compatible with the technology of light sources and detectors. Outline • Two level system: Spin and Light Polarization • Introduction to energy levels and optical transitions in SCQDs • The bright and dark excitons as matter two level systems – Writing the exciton spin state by a polarized light pulse tuned into excitonic resonances. – Reading its spin state by a second polarized light pulse, resonantly tuned into biexcitonic resonances. – Manipulating its spin state by a third polarized and/or detuned pulse. Two level system and the Bloch Sphere | 0 |1 | | | , are complex amplitudes | |2 | |2 1 is described by a po int on the Bloch sphere (| i |) 1/ 2 1/ 2(| |) (| |) 1/ 2 1/ 2(| i |) | classical bit (0 or 1)– quantum bit (qubit – Bloch sphere) • Jones vector: x y x 2 y • General solution to Maxwell equations for the direction of the electric field vector of a photon is an ellipse Linear Circular Technion – Israel Institute of Technology, Physics Department and Solid State Institute Elliptical 5 Polarization – Poincare’ sphere Poincare sphere Stokes parameters s0 , s1 , s2 , s3 H V s1 H V s2 DD DD s3 RL RL s0 H V R L D D Information can be encoded in the photon’s polarization state. 4 measurements are required to determine the full polarization state of light: a 2x2 density matrix V H Selection rules for optical transitions in semiconductor QDs 1 2 ; Conduction Band atomic s like 1 2 ~1.25 eV 3 2 3 2 3 e ; 2 ; ; 1 27 e 1 2 e 1 2 e e e e he e e e e e e e e e e e e Valence Band atomic p like hh ~0.05 eV lh e ~0.3 eV so 0,0,00 1212, ,12 12 1,1,1 1 3 2 , 32 32 promoting electron leaving hole of opposite ch arg e and spin 32 ,32 , 3232 STM (scanning tunneling microscope) images self assembled dots Not all the same, but live forever and can be put into high Q microcavities, easily Single Quantum Dot - Photoluminescence 2nm GaAs GaAs 1.5 monolayer InAs (PCI) GaAs GaAs Off resonance excitation P S h emission due to radiative recombination Spin interaction of charge carriers • Two electrons (holes) non-interacting spin states: 1 2 1 2 32 32 12 32 , Total spin: 1(3) 1 2 12 32 32 , 1 2 1(3) 32 , 12 32 1 2 32 0 30 (15) meV 0 • Electrons (holes) singlet state: Energy S S • Electrons (holes) triplet states: Spin blockaded , T+1(+3) , T-1(-3) T0 e-e (h-h) exchange ~5meV Quantum dot e-h pair (exciton) states Non interacting Isotropic electron-hole exchange Anisotropic electron-hole exchange a Bright Exciton 3 3 1 1 2 2 1 2 2 1 3 2 Δ1 ≈ 0.03meV V s Δ0 ≈ 0.3meV 12 2 23 12 2 Dark Exciton Dark exciton: Ground- state, Optically inactive, quantum two level system H a s Δ2 ≈ 0.001meV The dark exciton’s advantages • Its lifetime is long – comparable to that of a single electron or hole. • It is neutral and therefore less sensitive than charged particles to fluctuating electric fields. • Due to its fine structure and smaller g-factor, it is more protected than the electron or hole from fluctuating magnetic fields, especially where no external magnetic field is applied. as an in-matter qubit But how can it be addressed? E. Poem et al., Nature Physics ( November 2010) Biexciton excitation spectrum R Se Te V P S Th Sh i X S0 1 i D H S P I D L XX P0 Te1Th 3 Te S h S eTh Te 0Th 0 We can generate any of these biexciton spin states by tuning the energy and polarization of the laser. Se S h X P0 E Experimental setup Polarizing beam splitter First monochromator and CCD camera/Detector Spectral Two channel arbitrary polarization rotator Filter H V Second monochromator And detector Beam combiner Second pulse laser He Objective Quantum Dot Quantum Dot Wetting layer Quantum Dot First pulse laser Substrate Sample Delay line XX 0* XX 0 2nd pulse 1 2 1 2 H V D H X θ 0* R 1 2 1st pulse V X V 0 H 0 L D 1st pulse 1 2 P0(θ,) ‘Writing’ the spin with the 1st photonA 1i R R -LLL V R R H 2 2 X0 i ∆=30µev 2 1 2 S A Poincare sphere Bloch sphere S ‘Reading’ the spin with the 2nd photon Se T h Poincare XX 0* Se I(XX0) R Th Bloch X0 Time resolved, two-photon PL measurement XX0TT, X0P excitation 600 5 500 t [ps] 300 3 200 2 100 0 [integated Counts/min] -100 XX0T0 XX0 XX0T3 5 2 0 6 x 10 XX T3 2 XX0T0 1 0 1.2805 1.281 2 XX0 5 X-1 X0 6 X0 X+1 1.2815 1.282 1.2825 E [eV] 1.283 1.2835 1.2865 1.287 1 [103 counts/min] 4 400 Quasi-resonant Resonant Conclusions so far… • We demonstrate for the first time that the exciton spin can be ‘written’ in any arbitrary coherent superposition of its symmetric and anti-symmetric spin eigenstates by an elliptically polarized short laser pulse. • We showed that by tuning a second polarized laser pulse to a biexcitonic resonance, the exciton spin can be faithfully ‘readout’. • Y. Benny, et al, "Coherent optical writing and reading of the exciton spin state in single quantum dots " (arXiv:1009.5463v1 [quant-ph]28 Sep 2010), PRL 2011. March 31, 2011, Aussois, France E. Poem, Y. Kodriano, Y. Benny, C. Tradonsky, N. H. Lindner, J. E. Avron and D. Galushko The Physics Department and The Solid State Institute, Technion-Israel Institute of Technology, Haifa, 32000, Israel B. D. Gerardot and P. M. Petroff Materials Department, University of California Santa Barbara, CA, 93106, USA Technion – Israel Institute of Technology Physics Department and Solid State Institute Summary: