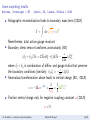Download Gravity in lower dimensions

Gravity in lower dimensions
Daniel Grumiller
Institute for Theoretical Physics
Vienna University of Technology
Uppsala University, December 2008
Outline
Why lower-dimensional gravity?
Which 2D theory?
Which 3D theory?
How to quantize 3D gravity?
What next?
D. Grumiller — Gravity in lower dimensions
2/42
Outline
Why lower-dimensional gravity?
Which 2D theory?
Which 3D theory?
How to quantize 3D gravity?
What next?
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
3/42
Quantum gravity
The Holy Grail of theoretical physics
There is a lot we do know about quantum gravity already
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
4/42
Quantum gravity
The Holy Grail of theoretical physics
There is a lot we do know about quantum gravity already
I
It should exist in some form
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
4/42
Quantum gravity
The Holy Grail of theoretical physics
There is a lot we do know about quantum gravity already
I
I
It should exist in some form
String theory: (perturbative) theory of quantum gravity
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
4/42
Quantum gravity
The Holy Grail of theoretical physics
There is a lot we do know about quantum gravity already
I
I
I
It should exist in some form
String theory: (perturbative) theory of quantum gravity
Microscopic understanding of extremal BH entropy
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
4/42
Quantum gravity
The Holy Grail of theoretical physics
There is a lot we do know about quantum gravity already
I
I
I
I
It should exist in some form
String theory: (perturbative) theory of quantum gravity
Microscopic understanding of extremal BH entropy
Conceptual insight — information loss problem resolved
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
4/42
Quantum gravity
The Holy Grail of theoretical physics
There is a lot we do know about quantum gravity already
I
I
I
I
It should exist in some form
String theory: (perturbative) theory of quantum gravity
Microscopic understanding of extremal BH entropy
Conceptual insight — information loss problem resolved
There is a lot we still do not know about quantum gravity
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
4/42
Quantum gravity
The Holy Grail of theoretical physics
There is a lot we do know about quantum gravity already
I
I
I
I
It should exist in some form
String theory: (perturbative) theory of quantum gravity
Microscopic understanding of extremal BH entropy
Conceptual insight — information loss problem resolved
There is a lot we still do not know about quantum gravity
I
Reasonable alternatives to string theory?
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
4/42
Quantum gravity
The Holy Grail of theoretical physics
There is a lot we do know about quantum gravity already
I
I
I
I
It should exist in some form
String theory: (perturbative) theory of quantum gravity
Microscopic understanding of extremal BH entropy
Conceptual insight — information loss problem resolved
There is a lot we still do not know about quantum gravity
I
I
Reasonable alternatives to string theory?
Non-perturbative understanding of quantum gravity?
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
4/42
Quantum gravity
The Holy Grail of theoretical physics
There is a lot we do know about quantum gravity already
I
I
I
I
It should exist in some form
String theory: (perturbative) theory of quantum gravity
Microscopic understanding of extremal BH entropy
Conceptual insight — information loss problem resolved
There is a lot we still do not know about quantum gravity
I
I
I
Reasonable alternatives to string theory?
Non-perturbative understanding of quantum gravity?
Microscopic understanding of non-extremal BH entropy?
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
4/42
Quantum gravity
The Holy Grail of theoretical physics
There is a lot we do know about quantum gravity already
I
I
I
I
It should exist in some form
String theory: (perturbative) theory of quantum gravity
Microscopic understanding of extremal BH entropy
Conceptual insight — information loss problem resolved
There is a lot we still do not know about quantum gravity
I
I
I
I
Reasonable alternatives to string theory?
Non-perturbative understanding of quantum gravity?
Microscopic understanding of non-extremal BH entropy?
Experimental signatures? Data?
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
4/42
Gravity in lower dimensions
2
2
−1)
components in D dimensions:
Riemann-tensor D (D
12
I 11D: 1210 (1144 Weyl and 66 Ricci)
I 10D: 825 (770 Weyl and 55 Ricci)
I 5D: 50 (35 Weyl and 15 Ricci)
I 4D: 20 (10 Weyl and 10 Ricci)
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
5/42
Gravity in lower dimensions
2
2
−1)
components in D dimensions:
Riemann-tensor D (D
12
I 11D: 1210 (1144 Weyl and 66 Ricci)
I 10D: 825 (770 Weyl and 55 Ricci)
I 5D: 50 (35 Weyl and 15 Ricci)
I 4D: 20 (10 Weyl and 10 Ricci)
I 3D: 6 (Ricci)
I 2D: 1 (Ricci scalar)
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
5/42
Gravity in lower dimensions
2
2
−1)
components in D dimensions:
Riemann-tensor D (D
12
I 11D: 1210 (1144 Weyl and 66 Ricci)
I 10D: 825 (770 Weyl and 55 Ricci)
I 5D: 50 (35 Weyl and 15 Ricci)
I 4D: 20 (10 Weyl and 10 Ricci)
I 3D: 6 (Ricci)
I 2D: 1 (Ricci scalar)
I
2D: lowest dimension exhibiting black holes (BHs)
I
Simplest gravitational theories with BHs in 2D
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
5/42
Gravity in lower dimensions
2
2
−1)
components in D dimensions:
Riemann-tensor D (D
12
I 11D: 1210 (1144 Weyl and 66 Ricci)
I 10D: 825 (770 Weyl and 55 Ricci)
I 5D: 50 (35 Weyl and 15 Ricci)
I 4D: 20 (10 Weyl and 10 Ricci)
I 3D: 6 (Ricci)
I 2D: 1 (Ricci scalar)
I
2D: lowest dimension exhibiting black holes (BHs)
I
Simplest gravitational theories with BHs in 2D
I
3D: lowest dimension exhibiting BHs and gravitons
I
Simplest gravitational theories with BHs and gravitons in 3D
D. Grumiller — Gravity in lower dimensions
Why lower-dimensional gravity?
5/42
Outline
Why lower-dimensional gravity?
Which 2D theory?
Which 3D theory?
How to quantize 3D gravity?
What next?
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
6/42
Attempt 1: Einstein–Hilbert in and near two dimensions
Let us start with the simplest attempt. Einstein-Hilbert action in 2
dimensions:
Z
p
1
1
d2 x |g| R =
(1 − γ)
IEH =
16π G
2G
I
Action is topological
I
No equations of motion
I
Formal counting of number of gravitons: -1
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
7/42
Attempt 1: Einstein–Hilbert in and near two dimensions
Let us continue with the next simplest attempt. Einstein-Hilbert
action in 2+ dimensions:
Z
p
1
IEH =
d2+ x |g| R
16π G
I
Weinberg: theory is asymptotically safe
I
Mann: limit → 0 should be possible and lead to 2D dilaton gravity
I
DG, Jackiw: limit → 0 yields Liouville gravity
Z
p 1
d2 x |g| XR − (∇X)2 + λe−2X
lim IEH =
→0
16π G2
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
7/42
Attempt 1: Einstein–Hilbert in and near two dimensions
Let us continue with the next simplest attempt. Einstein-Hilbert
action in 2+ dimensions:
Z
p
1
IEH =
d2+ x |g| R
16π G
I
Weinberg: theory is asymptotically safe
I
Mann: limit → 0 should be possible and lead to 2D dilaton gravity
I
DG, Jackiw: limit → 0 yields Liouville gravity
Z
p 1
d2 x |g| XR − (∇X)2 + λe−2X
lim IEH =
→0
16π G2
Result of attempt 1:
A specific 2D dilaton gravity model
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
7/42
Attempt 2: Gravity as a gauge theory and the Jackiw-Teitelboim model
Jackiw, Teitelboim (Bunster): (A)dS2 gauge theory
[Pa , Pb ] = Λ ab J
[Pa , J] = a b Pb
describes constant curvature gravity in 2D.
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
Algorithm:
8/42
Attempt 2: Gravity as a gauge theory and the Jackiw-Teitelboim model
Jackiw, Teitelboim (Bunster): (A)dS2 gauge theory
[Pa , Pb ] = Λ ab J
[Pa , J] = a b Pb
describes constant curvature gravity in 2D.
Algorithm:
I Start with SO(1, 2) connection A = ea Pa + ωJ
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
8/42
Attempt 2: Gravity as a gauge theory and the Jackiw-Teitelboim model
Jackiw, Teitelboim (Bunster): (A)dS2 gauge theory
[Pa , Pb ] = Λ ab J
[Pa , J] = a b Pb
describes constant curvature gravity in 2D.
Algorithm:
I Start with SO(1, 2) connection A = ea Pa + ωJ
I Take field strength F = dA + 1 [A, A] and coadjoint scalar X
2
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
8/42
Attempt 2: Gravity as a gauge theory and the Jackiw-Teitelboim model
Jackiw, Teitelboim (Bunster): (A)dS2 gauge theory
[Pa , Pb ] = Λ ab J
[Pa , J] = a b Pb
describes constant curvature gravity in 2D.
Algorithm:
I Start with SO(1, 2) connection A = ea Pa + ωJ
I Take field strength F = dA + 1 [A, A] and coadjoint scalar X
2
I Construct non-abelian BF theory
Z
Z h
i
A
I = XA F =
Xa (dea + a b ω ∧ eb ) + X dω + ab ea ∧ eb ΛX
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
8/42
Attempt 2: Gravity as a gauge theory and the Jackiw-Teitelboim model
Jackiw, Teitelboim (Bunster): (A)dS2 gauge theory
[Pa , Pb ] = Λ ab J
[Pa , J] = a b Pb
describes constant curvature gravity in 2D.
Algorithm:
I Start with SO(1, 2) connection A = ea Pa + ωJ
I Take field strength F = dA + 1 [A, A] and coadjoint scalar X
2
I Construct non-abelian BF theory
Z
Z h
i
A
I = XA F =
Xa (dea + a b ω ∧ eb ) + X dω + ab ea ∧ eb ΛX
I
Eliminate Xa (Torsion constraint) and ω (Levi-Civita connection)
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
8/42
Attempt 2: Gravity as a gauge theory and the Jackiw-Teitelboim model
Jackiw, Teitelboim (Bunster): (A)dS2 gauge theory
[Pa , Pb ] = Λ ab J
[Pa , J] = a b Pb
describes constant curvature gravity in 2D.
Algorithm:
I Start with SO(1, 2) connection A = ea Pa + ωJ
I Take field strength F = dA + 1 [A, A] and coadjoint scalar X
2
I Construct non-abelian BF theory
Z
Z h
i
A
I = XA F =
Xa (dea + a b ω ∧ eb ) + X dω + ab ea ∧ eb ΛX
I
I
Eliminate Xa (Torsion constraint) and ω (Levi-Civita connection)
Obtain the second order action
Z
√
1
I=
d2 x −g X [R − Λ]
16π G2
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
8/42
Attempt 2: Gravity as a gauge theory and the Jackiw-Teitelboim model
Jackiw, Teitelboim (Bunster): (A)dS2 gauge theory
[Pa , J] = a b Pb
[Pa , Pb ] = Λ ab J
describes constant curvature gravity in 2D.
Algorithm:
I Start with SO(1, 2) connection A = ea Pa + ωJ
I Take field strength F = dA + 1 [A, A] and coadjoint scalar X
2
I Construct non-abelian BF theory
Z
Z h
i
A
I = XA F =
Xa (dea + a b ω ∧ eb ) + X dω + ab ea ∧ eb ΛX
I
I
Eliminate Xa (Torsion constraint) and ω (Levi-Civita connection)
Obtain the second order action
Z
√
1
I=
d2 x −g X [R − Λ]
16π G2
Result of attempt 2:
A specific 2D dilaton gravity model
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
8/42
Attempt 3: Dimensional reduction
For example: spherical reduction from D dimensions
Line element adapted to spherical symmetry:
ds2 =
(D)
gµν
|{z}
full metric
dxµ dxν = gαβ (xγ ) dxα dxβ − φ2 (xα ) dΩ2SD−2 ,
| {z }
| {z }
D. Grumiller — Gravity in lower dimensions
2D metric
Which 2D theory?
surface area
9/42
Attempt 3: Dimensional reduction
For example: spherical reduction from D dimensions
Line element adapted to spherical symmetry:
ds2 =
(D)
gµν
|{z}
full metric
dxµ dxν = gαβ (xγ ) dxα dxβ − φ2 (xα ) dΩ2SD−2 ,
| {z }
| {z }
surface area
2D metric
p
Insert into D-dimensional EH action IEH = κ dD x −g (D) R(D) :
Z
h
i
2π (D−1)/2
(D − 2)(D − 3)
D−2
2 √
2
IEH = κ
−g
φ
d
x
R
+
(∇φ)
−
1
φ2
Γ( D−1
2 )
R
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
9/42
Attempt 3: Dimensional reduction
For example: spherical reduction from D dimensions
Line element adapted to spherical symmetry:
ds2 =
(D)
gµν
|{z}
full metric
dxµ dxν = gαβ (xγ ) dxα dxβ − φ2 (xα ) dΩ2SD−2 ,
| {z }
| {z }
surface area
2D metric
p
Insert into D-dimensional EH action IEH = κ dD x −g (D) R(D) :
Z
h
i
2π (D−1)/2
(D − 2)(D − 3)
D−2
2 √
2
IEH = κ
−g
φ
d
x
R
+
(∇φ)
−
1
φ2
Γ( D−1
2 )
R
Cosmetic redefinition X ∝ (λφ)D−2 :
Z
i
√ h
1
D−3
IEH =
d2 x −g XR +
(∇X)2 − λ2 X (D−4)/(D−2)
16π G2
(D − 2)X
Result of attempt 3:
A specific class of 2D dilaton gravity models
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
9/42
Attempt 4: Poincare gauge theory and higher power curvature theories
Basic idea: since EH is trivial consider f (R) theories or/and theories with
torsion or/and theories with non-metricity
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
10/42
Attempt 4: Poincare gauge theory and higher power curvature theories
Basic idea: since EH is trivial consider f (R) theories or/and theories with
torsion or/and theories with non-metricity
I Example: Katanaev-Volovich model (Poincare gauge theory)
Z
√ IKV ∼ d2 x −g αT 2 + βR2
I
Kummer, Schwarz: bring into first order form:
Z h
i
IKV ∼
Xa (dea + a b ω ∧ eb ) + X dω + ab ea ∧ eb (αX a Xa + βX 2 )
I
Use same algorithm as before to convert into second order action:
Z
i
√ h
1
IKV =
d2 x −g XR + α(∇X)2 + βX 2
16π G2
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
10/42
Attempt 4: Poincare gauge theory and higher power curvature theories
Basic idea: since EH is trivial consider f (R) theories or/and theories with
torsion or/and theories with non-metricity
I Example: Katanaev-Volovich model (Poincare gauge theory)
Z
√ IKV ∼ d2 x −g αT 2 + βR2
I
Kummer, Schwarz: bring into first order form:
Z h
i
IKV ∼
Xa (dea + a b ω ∧ eb ) + X dω + ab ea ∧ eb (αX a Xa + βX 2 )
I
Use same algorithm as before to convert into second order action:
Z
i
√ h
1
IKV =
d2 x −g XR + α(∇X)2 + βX 2
16π G2
Result of attempt 4:
A specific 2D dilaton gravity model
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
10/42
Attempt 5: Strings in two dimensions
Conformal invariance of the σ model
Z
p Iσ ∝ d2 ξ |h| gµν hij ∂i xµ ∂j xν + α0 φR + . . .
requires vanishing of β-functions
β φ ∝ −4b2 − 4(∇φ)2 + 4φ + R + . . .
g
βµν
∝ Rµν + 2∇µ ∇ν φ + . . .
g
Conditions β φ = βµν
= 0 follow from target space action
Z
i
√ h
1
1
Itarget =
d2 x −g XR +
(∇X)2 − 4b2
16π G2
X
where X = e−2φ
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
11/42
Attempt 5: Strings in two dimensions
Conformal invariance of the σ model
Z
p Iσ ∝ d2 ξ |h| gµν hij ∂i xµ ∂j xν + α0 φR + . . .
requires vanishing of β-functions
β φ ∝ −4b2 − 4(∇φ)2 + 4φ + R + . . .
g
βµν
∝ Rµν + 2∇µ ∇ν φ + . . .
g
Conditions β φ = βµν
= 0 follow from target space action
Z
i
√ h
1
1
Itarget =
d2 x −g XR +
(∇X)2 − 4b2
16π G2
X
where X = e−2φ
Result of attempt 5:
A specific 2D dilaton gravity model
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
11/42
Synthesis of all attempts: Dilaton gravity in two dimensions
Second order action:
Z
p 1
d2 x |g| XR − U (X)(∇X)2 − V (X)
I=
16π G2 M
Z
p
1
−
dx |γ| [XK − S(X)] + I (m)
8π G2 ∂M
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
12/42
Synthesis of all attempts: Dilaton gravity in two dimensions
Second order action:
Z
p 1
d2 x |g| XR − U (X)(∇X)2 − V (X)
I=
16π G2 M
Z
p
1
−
dx |γ| [XK − S(X)] + I (m)
8π G2 ∂M
I
Dilaton X defined by its coupling to curvature R
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
12/42
Synthesis of all attempts: Dilaton gravity in two dimensions
Second order action:
Z
p 1
d2 x |g| XR − U (X)(∇X)2 − V (X)
I=
16π G2 M
Z
p
1
−
dx |γ| [XK − S(X)] + I (m)
8π G2 ∂M
I
I
Dilaton X defined by its coupling to curvature R
Kinetic term (∇X)2 contains coupling function U (X)
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
12/42
Synthesis of all attempts: Dilaton gravity in two dimensions
Second order action:
Z
p 1
d2 x |g| XR − U (X)(∇X)2 − V (X)
I=
16π G2 M
Z
p
1
−
dx |γ| [XK − S(X)] + I (m)
8π G2 ∂M
I
I
I
Dilaton X defined by its coupling to curvature R
Kinetic term (∇X)2 contains coupling function U (X)
Self-interaction potential V (X) leads to non-trivial geometries
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
12/42
Synthesis of all attempts: Dilaton gravity in two dimensions
Second order action:
Z
p 1
d2 x |g| XR − U (X)(∇X)2 − V (X)
I=
16π G2 M
Z
p
1
−
dx |γ| [XK − S(X)] + I (m)
8π G2 ∂M
I
I
I
I
Dilaton X defined by its coupling to curvature R
Kinetic term (∇X)2 contains coupling function U (X)
Self-interaction potential V (X) leads to non-trivial geometries
Gibbons–Hawking–York boundary term guarantees Dirichlet boundary
problem for metric
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
12/42
Synthesis of all attempts: Dilaton gravity in two dimensions
Second order action:
Z
p 1
d2 x |g| XR − U (X)(∇X)2 − V (X)
I=
16π G2 M
Z
p
1
−
dx |γ| [XK − S(X)] + I (m)
8π G2 ∂M
I
I
I
I
I
Dilaton X defined by its coupling to curvature R
Kinetic term (∇X)2 contains coupling function U (X)
Self-interaction potential V (X) leads to non-trivial geometries
Gibbons–Hawking–York boundary term guarantees Dirichlet boundary
problem for metric
Hamilton–Jacobi counterterm contains superpotential S(X)
Z X
R
Ry
2
− X U (y) dy
S(X) = e
V (y)e U (z) dz dy
and guarantees well-defined variational principle δI = 0
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
12/42
Synthesis of all attempts: Dilaton gravity in two dimensions
Second order action:
Z
p 1
d2 x |g| XR − U (X)(∇X)2 − V (X)
I=
16π G2 M
Z
p
1
−
dx |γ| [XK − S(X)] + I (m)
8π G2 ∂M
I
I
I
I
I
I
Dilaton X defined by its coupling to curvature R
Kinetic term (∇X)2 contains coupling function U (X)
Self-interaction potential V (X) leads to non-trivial geometries
Gibbons–Hawking–York boundary term guarantees Dirichlet boundary
problem for metric
Hamilton–Jacobi counterterm contains superpotential S(X)
Z X
R
Ry
2
− X U (y) dy
S(X) = e
V (y)e U (z) dz dy
and guarantees well-defined variational principle δI = 0
Interesting option: couple 2D dilaton gravity to matter
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
12/42
Recent example: AdS2 holography
Two dimensions supposed to be the simplest dimension with geometry, and yet...
I
I
I
extremal black holes universally include AdS2 factor
funnily, AdS3 holography more straightforward
study charged Jackiw–Teitelboim model as example
Z
L2 2
α
8
−2φ
2 √
F
IJT =
d x −g e
R+ 2 −
2π
L
4
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
13/42
Recent example: AdS2 holography
Two dimensions supposed to be the simplest dimension with geometry, and yet...
I
extremal black holes universally include AdS2 factor
funnily, AdS3 holography more straightforward
study charged Jackiw–Teitelboim model as example
Z
8
L2 2
α
−2φ
2 √
R+ 2 −
F
IJT =
d x −g e
2π
L
4
I
Metric g has signature −, + and Ricci-scalar R< 0 for AdS
I
I
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
13/42
Recent example: AdS2 holography
Two dimensions supposed to be the simplest dimension with geometry, and yet...
I
I
I
I
I
extremal black holes universally include AdS2 factor
funnily, AdS3 holography more straightforward
study charged Jackiw–Teitelboim model as example
Z
8
L2 2
α
−2φ
2 √
R+ 2 −
F
IJT =
d x −g e
2π
L
4
Metric g has signature −, + and Ricci-scalar R< 0 for AdS
Maxwell field strength Fµν = 2E εµν dual to electric field E
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
13/42
Recent example: AdS2 holography
Two dimensions supposed to be the simplest dimension with geometry, and yet...
I
I
I
I
I
I
extremal black holes universally include AdS2 factor
funnily, AdS3 holography more straightforward
study charged Jackiw–Teitelboim model as example
Z
8
L2 2
α
−2φ
2 √
R+ 2 −
F
IJT =
d x −g e
2π
L
4
Metric g has signature −, + and Ricci-scalar R< 0 for AdS
Maxwell field strength Fµν = 2E εµν dual to electric field E
Dilaton φ has no kinetic term and no coupling to gauge field
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
13/42
Recent example: AdS2 holography
Two dimensions supposed to be the simplest dimension with geometry, and yet...
I
I
I
I
I
I
I
extremal black holes universally include AdS2 factor
funnily, AdS3 holography more straightforward
study charged Jackiw–Teitelboim model as example
Z
8
L2 2
α
−2φ
2 √
R+ 2 −
F
IJT =
d x −g e
2π
L
4
Metric g has signature −, + and Ricci-scalar R< 0 for AdS
Maxwell field strength Fµν = 2E εµν dual to electric field E
Dilaton φ has no kinetic term and no coupling to gauge field
Cosmological constant Λ = − L82 parameterized by AdS radius L
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
13/42
Recent example: AdS2 holography
Two dimensions supposed to be the simplest dimension with geometry, and yet...
I
I
I
I
I
I
I
I
extremal black holes universally include AdS2 factor
funnily, AdS3 holography more straightforward
study charged Jackiw–Teitelboim model as example
Z
α
8
L2 2
2 √
−2φ
d x −g e
R+ 2 −
F
IJT =
2π
L
4
Metric g has signature −, + and Ricci-scalar R< 0 for AdS
Maxwell field strength Fµν = 2E εµν dual to electric field E
Dilaton φ has no kinetic term and no coupling to gauge field
Cosmological constant Λ = − L82 parameterized by AdS radius L
Coupling constant α usually is positive
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
13/42
Recent example: AdS2 holography
Two dimensions supposed to be the simplest dimension with geometry, and yet...
I
I
I
I
I
I
I
I
I
extremal black holes universally include AdS2 factor
funnily, AdS3 holography more straightforward
study charged Jackiw–Teitelboim model as example
Z
α
8
L2 2
2 √
−2φ
d x −g e
R+ 2 −
F
IJT =
2π
L
4
Metric g has signature −, + and Ricci-scalar R< 0 for AdS
Maxwell field strength Fµν = 2E εµν dual to electric field E
Dilaton φ has no kinetic term and no coupling to gauge field
Cosmological constant Λ = − L82 parameterized by AdS radius L
Coupling constant α usually is positive
δφ EOM: R = − L82
⇒
AdS2 !
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
13/42
Recent example: AdS2 holography
Two dimensions supposed to be the simplest dimension with geometry, and yet...
I
I
I
I
I
I
I
I
I
I
extremal black holes universally include AdS2 factor
funnily, AdS3 holography more straightforward
study charged Jackiw–Teitelboim model as example
Z
α
8
L2 2
2 √
−2φ
d x −g e
R+ 2 −
F
IJT =
2π
L
4
Metric g has signature −, + and Ricci-scalar R< 0 for AdS
Maxwell field strength Fµν = 2E εµν dual to electric field E
Dilaton φ has no kinetic term and no coupling to gauge field
Cosmological constant Λ = − L82 parameterized by AdS radius L
Coupling constant α usually is positive
δφ EOM: R = − L82
⇒
AdS2 !
µν
δA EOM: ∇µ F = 0 ⇒
E = constant
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
13/42
Recent example: AdS2 holography
Two dimensions supposed to be the simplest dimension with geometry, and yet...
I
I
I
I
I
I
I
I
I
I
I
extremal black holes universally include AdS2 factor
funnily, AdS3 holography more straightforward
study charged Jackiw–Teitelboim model as example
Z
α
8
L2 2
2 √
−2φ
d x −g e
R+ 2 −
F
IJT =
2π
L
4
Metric g has signature −, + and Ricci-scalar R< 0 for AdS
Maxwell field strength Fµν = 2E εµν dual to electric field E
Dilaton φ has no kinetic term and no coupling to gauge field
Cosmological constant Λ = − L82 parameterized by AdS radius L
Coupling constant α usually is positive
δφ EOM: R = − L82
⇒
AdS2 !
µν
δA EOM: ∇µ F = 0 ⇒
E = constant
δg EOM: complicated for non-constant dilaton...
∇µ ∇ν e−2φ − gµν ∇2 e−2φ +
D. Grumiller — Gravity in lower dimensions
4 −2φ
L2 λ
L2
e
g
+
F
F
−
gµν F 2 = 0
µν
µ
νλ
L2
2
8
Which 2D theory?
13/42
Recent example: AdS2 holography
Two dimensions supposed to be the simplest dimension with geometry, and yet...
I
I
I
I
I
I
I
I
I
I
I
extremal black holes universally include AdS2 factor
funnily, AdS3 holography more straightforward
study charged Jackiw–Teitelboim model as example
Z
α
8
L2 2
2 √
−2φ
d x −g e
R+ 2 −
F
IJT =
2π
L
4
Metric g has signature −, + and Ricci-scalar R< 0 for AdS
Maxwell field strength Fµν = 2E εµν dual to electric field E
Dilaton φ has no kinetic term and no coupling to gauge field
Cosmological constant Λ = − L82 parameterized by AdS radius L
Coupling constant α usually is positive
δφ EOM: R = − L82
⇒
AdS2 !
µν
δA EOM: ∇µ F = 0 ⇒
E = constant
4
δg EOM: ...but simple for constant dilaton: e−2φ = L4 E 2
∇µ ∇ν e−2φ − gµν ∇2 e−2φ +
D. Grumiller — Gravity in lower dimensions
4 −2φ
L2 λ
L2
e
g
+
F
F
−
gµν F 2 = 0
µν
µ
νλ
L2
2
8
Which 2D theory?
13/42
Some surprising results
Hartman, Strominger = HS
I
Castro, DG, Larsen, McNees = CGLM
Holographic renormalization leads to boundary mass term (CGLM)
Z
p
I ∼ dx |γ| mA2
Nevertheless, total action gauge invariant
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
14/42
Some surprising results
Hartman, Strominger = HS
I
I
Castro, DG, Larsen, McNees = CGLM
Holographic renormalization leads to boundary mass term (CGLM)
Z
p
I ∼ dx |γ| mA2
Nevertheless, total action gauge invariant
Boundary stress tensor transforms anomalously (HS)
c
(δξ + δλ ) Ttt = 2Ttt ∂t ξ + ξ∂t Ttt −
L∂ 3 ξ
24π t
where δξ + δλ is combination of diffeo- and gauge trafos that preserve
k
the boundary conditions (similarly: δλ Jt = − 4π
L∂t λ)
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
14/42
Some surprising results
Hartman, Strominger = HS
I
I
I
Castro, DG, Larsen, McNees = CGLM
Holographic renormalization leads to boundary mass term (CGLM)
Z
p
I ∼ dx |γ| mA2
Nevertheless, total action gauge invariant
Boundary stress tensor transforms anomalously (HS)
c
(δξ + δλ ) Ttt = 2Ttt ∂t ξ + ξ∂t Ttt −
L∂ 3 ξ
24π t
where δξ + δλ is combination of diffeo- and gauge trafos that preserve
k
the boundary conditions (similarly: δλ Jt = − 4π
L∂t λ)
Anomalous transformation above leads to central charge (HS, CGLM)
3
3
c = −24αe−2φ =
= kE 2 L2
G2
2
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
14/42
Some surprising results
Hartman, Strominger = HS
I
I
I
I
Castro, DG, Larsen, McNees = CGLM
Holographic renormalization leads to boundary mass term (CGLM)
Z
p
I ∼ dx |γ| mA2
Nevertheless, total action gauge invariant
Boundary stress tensor transforms anomalously (HS)
c
(δξ + δλ ) Ttt = 2Ttt ∂t ξ + ξ∂t Ttt −
L∂ 3 ξ
24π t
where δξ + δλ is combination of diffeo- and gauge trafos that preserve
k
the boundary conditions (similarly: δλ Jt = − 4π
L∂t λ)
Anomalous transformation above leads to central charge (HS, CGLM)
3
3
c = −24αe−2φ =
= kE 2 L2
G2
2
Positive central charge only for negative coupling constant α (CGLM)
α<0
D. Grumiller — Gravity in lower dimensions
Which 2D theory?
14/42
Outline
Why lower-dimensional gravity?
Which 2D theory?
Which 3D theory?
How to quantize 3D gravity?
What next?
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
15/42
Attempt 1: Einstein–Hilbert
As simple as possible... but not simpler!
Let us start with the simplest attempt. Einstein-Hilbert action:
Z
√
1
IEH =
d3 x −g R
16π G
Equations of motion:
Rµν = 0
Ricci-flat and therefore Riemann-flat – locally trivial!
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
16/42
Attempt 1: Einstein–Hilbert
As simple as possible... but not simpler!
Let us start with the simplest attempt. Einstein-Hilbert action:
Z
√
1
IEH =
d3 x −g R
16π G
Equations of motion:
Rµν = 0
Ricci-flat and therefore Riemann-flat – locally trivial!
Properties of Einstein-Hilbert
I
No gravitons (recall: in D dimensions D(D − 3)/2 gravitons)
I
No BHs
I
Einstein-Hilbert in 3D is too simple for us!
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
16/42
Attempt 2: Topologically massive gravity
Deser, Jackiw and Templeton found a way to introduce gravitons!
Let us now add a gravitational Chern–Simons term. TMG action:
Z
√
1
1 λµν ρ
2
ITMG = IEH +
ε
Γ λσ ∂µ Γσ νρ + Γσ µτ Γτ νρ
d3 x −g
16π G
2µ
3
Equations of motion:
1
Rµν + Cµν = 0
µ
with the Cotton tensor defined as
1
Cµν = εµ αβ ∇α Rβν + (µ ↔ ν)
2
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
17/42
Attempt 2: Topologically massive gravity
Deser, Jackiw and Templeton found a way to introduce gravitons!
Let us now add a gravitational Chern–Simons term. TMG action:
Z
√
1
1 λµν ρ
2
ITMG = IEH +
ε
Γ λσ ∂µ Γσ νρ + Γσ µτ Γτ νρ
d3 x −g
16π G
2µ
3
Equations of motion:
1
Rµν + Cµν = 0
µ
with the Cotton tensor defined as
1
Cµν = εµ αβ ∇α Rβν + (µ ↔ ν)
2
Properties of TMG
I
Gravitons! Reason: third derivatives in Cotton tensor!
I
No BHs
I
TMG is slightly too simple for us!
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
17/42
Attempt 3: Einstein–Hilbert–AdS
Bañados, Teitelboim and Zanelli (and Henneaux) taught us how to get 3D BHs
Add negative cosmological constant to Einstein-Hilbert action:
Z
√
1
2
IΛEH =
d3 x −g R + 2
16π G
`
Equations of motion:
1
1
Gµν = Rµν − gµν R − 2 gµν = 0
2
`
Particular solutions: BTZ BH with line-element
ds2BTZ = −
2
2
(r2 − r+
)(r2 − r−
) 2
`2 r2
r+ r− 2
dt
+
dr2 + r2 dφ −
dt
2
2
2
2
2
2
` r
(r − r+ )(r − r− )
`r2
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
18/42
Attempt 3: Einstein–Hilbert–AdS
Bañados, Teitelboim and Zanelli (and Henneaux) taught us how to get 3D BHs
Add negative cosmological constant to Einstein-Hilbert action:
Z
√
1
2
IΛEH =
d3 x −g R + 2
16π G
`
Equations of motion:
1
1
Gµν = Rµν − gµν R − 2 gµν = 0
2
`
Particular solutions: BTZ BH with line-element
ds2BTZ = −
2
2
(r2 − r+
)(r2 − r−
) 2
`2 r2
r+ r− 2
dt
+
dr2 + r2 dφ −
dt
2
2
2
2
2
2
` r
(r − r+ )(r − r− )
`r2
Properties of Einstein-Hilbert-AdS
I
No gravitons
I
Rotating BH solutions that asymptote to AdS3 !
I
Adding a negative cosmological constant produces BH solutions!
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
18/42
Cosmological topologically massive gravity
CTMG is a 3D theory with BHs and gravitons!
We want a 3D theory with gravitons and BHs and therefore take CTMG
action
Z
i
√ h
1
2
1 λµν ρ
2
ICTMG =
d3 x −g R + 2 +
ε
Γ λσ ∂µ Γσ νρ + Γσ µτ Γτ νρ
16π G
`
2µ
3
Equations of motion:
Gµν +
D. Grumiller — Gravity in lower dimensions
1
Cµν = 0
µ
Which 3D theory?
19/42
Cosmological topologically massive gravity
CTMG is a 3D theory with BHs and gravitons!
We want a 3D theory with gravitons and BHs and therefore take CTMG
action
Z
i
√ h
1
2
1 λµν ρ
2
ICTMG =
d3 x −g R + 2 +
ε
Γ λσ ∂µ Γσ νρ + Γσ µτ Γτ νρ
16π G
`
2µ
3
Equations of motion:
Gµν +
1
Cµν = 0
µ
Properties of CTMG
I
Gravitons!
I
BHs!
I
CTMG is just perfect for us. Study this theory!
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
19/42
Einstein sector of the classical theory
Solutions of Einstein’s equations
↔
Gµν = 0
R=−
6
`2
also have vanishing Cotton tensor
Cµν = 0
and therefore are solutions of CTMG.
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
20/42
Einstein sector of the classical theory
Solutions of Einstein’s equations
↔
Gµν = 0
R=−
6
`2
also have vanishing Cotton tensor
Cµν = 0
and therefore are solutions of CTMG.
This sector of solutions contains
I BTZ BH
I Pure AdS
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
20/42
Einstein sector of the classical theory
Solutions of Einstein’s equations
↔
Gµν = 0
R=−
6
`2
also have vanishing Cotton tensor
Cµν = 0
and therefore are solutions of CTMG.
This sector of solutions contains
I BTZ BH
I Pure AdS
Line-element of pure AdS:
ds2AdS = ḡµν dxµ dxν = `2 − cosh2 ρ dτ 2 + sinh2 ρ dφ2 + dρ2
Isometry group: SL(2, R)L × SL(2, R)R
Useful to introduce light-cone coordinates u = τ + φ, v = τ − φ
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
20/42
AdS3 -algebra of Killing vectors
A technical reminder
The SL(2, R)L generators
L0 = i∂u
L±1 = ie±iu
h cosh 2ρ
sinh 2ρ
∂u −
1
i i
∂v ∓ ∂ρ
sinh 2ρ
2
obey the algebra
[L0 , L±1 ] = ∓L±1 ,
[L1 , L−1 ] = 2L0
and have the quadratic Casimir
1
L2 = (L1 L−1 + L−1 L1 ) − L20
2
The SL(2, R)R generators L̄0 , L̄±1 obey same algebra, but with
u ↔ v,
D. Grumiller — Gravity in lower dimensions
L ↔ L̄
Which 3D theory?
21/42
Cotton sector of the classical theory
Solutions of CTMG with
Gµν 6= 0
necessarily have also non-vanishing Cotton tensor
Cµν 6= 0
Few exact solutions of this type are known.
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
22/42
Cotton sector of the classical theory
Solutions of CTMG with
Gµν 6= 0
necessarily have also non-vanishing Cotton tensor
Cµν 6= 0
Few exact solutions of this type are known.
Perhaps most interesting solution:
I Warped AdS (stretched/squashed), see Bengtsson & Sandin
Line-element of space-like warped AdS:
ds2warped AdS =
`2
4ν 2
2
2
2
2
(du
+
sinh
ρ
dτ
)
+
dρ
−
cosh
ρ
dτ
+
ν2 + 3
ν2 + 3
Sidenote: null-warped AdS in holographic duals of cold atoms:
dy 2 + 2 dx+ dx− (dx− )2 ds2null warped AdS = `2
±
y2
y4
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
22/42
CTMG as particle mechanics problem
Stationary and axi-symmetric solutions
Stationarity plus axi-symmetry:
I Two commuting Killing vectors
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
23/42
CTMG as particle mechanics problem
Stationary and axi-symmetric solutions
Stationarity plus axi-symmetry:
I Two commuting Killing vectors
I Effectively reduce 2+1 dimensions to 1+0 dimensions
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
23/42
CTMG as particle mechanics problem
Stationary and axi-symmetric solutions
Stationarity plus axi-symmetry:
I Two commuting Killing vectors
I Effectively reduce 2+1 dimensions to 1+0 dimensions
I Like particle mechanics, but with up to three time derivatives
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
23/42
CTMG as particle mechanics problem
Stationary and axi-symmetric solutions
Stationarity plus axi-symmetry:
I Two commuting Killing vectors
I Effectively reduce 2+1 dimensions to 1+0 dimensions
I Like particle mechanics, but with up to three time derivatives
I Still surprisingly difficult to get exact solutions!
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
23/42
CTMG as particle mechanics problem
Stationary and axi-symmetric solutions
Stationarity plus axi-symmetry:
I Two commuting Killing vectors
I Effectively reduce 2+1 dimensions to 1+0 dimensions
I Like particle mechanics, but with up to three time derivatives
I Still surprisingly difficult to get exact solutions!
I Known solutions: AdS, BTZ, warped AdS
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
23/42
CTMG as particle mechanics problem
Stationary and axi-symmetric solutions
Stationarity plus axi-symmetry:
I Two commuting Killing vectors
I Effectively reduce 2+1 dimensions to 1+0 dimensions
I Like particle mechanics, but with up to three time derivatives
I Still surprisingly difficult to get exact solutions!
I Known solutions: AdS, BTZ, warped AdS
Reduced action (Clement):
Z
i
hζ
2
ζ2
IC [ζ, X i ] ∼ dρ
Ẋ i Ẋ j ηij − 2 +
ijk X i Ẋ j Ẍ k
2
ζ`
2µ
Here ζ is a Lagrange-multiplier and X i = (T, X, Y ) a Lorentzian 3-vector
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
23/42
CTMG as particle mechanics problem
Stationary and axi-symmetric solutions
Stationarity plus axi-symmetry:
I Two commuting Killing vectors
I Effectively reduce 2+1 dimensions to 1+0 dimensions
I Like particle mechanics, but with up to three time derivatives
I Still surprisingly difficult to get exact solutions!
I Known solutions: AdS, BTZ, warped AdS
Reduced action (Clement):
Z
i
hζ
2
ζ2
IC [ζ, X i ] ∼ dρ
Ẋ i Ẋ j ηij − 2 +
ijk X i Ẋ j Ẍ k
2
ζ`
2µ
Here ζ is a Lagrange-multiplier and X i = (T, X, Y ) a Lorentzian 3-vector
It could be rewarding to investigate this mechanical
problem systematically and numerically!
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
23/42
CTMG at the chiral point
...abbreviated as CCTMG
Definition: CTMG at the chiral point is CTMG with the tuning
µ` = 1
between the cosmological constant and the Chern–Simons coupling.
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
24/42
CTMG at the chiral point
...abbreviated as CCTMG
Definition: CTMG at the chiral point is CTMG with the tuning
µ` = 1
between the cosmological constant and the Chern–Simons coupling.
Why special?
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
24/42
CTMG at the chiral point
...abbreviated as CCTMG
Definition: CTMG at the chiral point is CTMG with the tuning
µ` = 1
between the cosmological constant and the Chern–Simons coupling.
Why special?
Calculating the central charges of the dual boundary CFT yields
cL =
1 3
1−
,
2G
µ`
cR =
1 3
1+
2G
µ`
cR =
3
G
Thus, at the chiral point we get
cL = 0 ,
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
24/42
CTMG at the chiral point
...abbreviated as CCTMG
Definition: CTMG at the chiral point is CTMG with the tuning
µ` = 1
between the cosmological constant and the Chern–Simons coupling.
Why special?
Calculating the central charges of the dual boundary CFT yields
cL =
1 3
1−
,
2G
µ`
cR =
1 3
1+
2G
µ`
cR =
3
G
Thus, at the chiral point we get
cL = 0 ,
Notes:
I Abbreviate “CTMG at the chiral point” as CCTMG
I CCTMG is also known as “chiral gravity”
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
24/42
Gravitons around AdS3 in CTMG
Linearization around AdS background
gµν = ḡµν + hµν
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
25/42
Gravitons around AdS3 in CTMG
Linearization around AdS background
gµν = ḡµν + hµν
leads to linearized EOM that are third order PDE
1 (1)
G(1)
C = (DR DL DM h)µν = 0
µν +
µ µν
(1)
with three mutually commuting first order operators
¯α,
(DL/R )µ ν = δµν ± ` εµ αν ∇
D. Grumiller — Gravity in lower dimensions
(DM )µ ν = δµν +
Which 3D theory?
1 αν ¯
εµ ∇α
µ
25/42
Gravitons around AdS3 in CTMG
Linearization around AdS background
gµν = ḡµν + hµν
leads to linearized EOM that are third order PDE
1 (1)
G(1)
C = (DR DL DM h)µν = 0
µν +
µ µν
(1)
with three mutually commuting first order operators
¯α,
(DL/R )µ ν = δµν ± ` εµ αν ∇
(DM )µ ν = δµν +
Three linearly independent solutions to (1):
DL hL µν = 0 ,
DR hR µν = 0 ,
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
1 αν ¯
εµ ∇α
µ
D M hM
µν
=0
25/42
Gravitons around AdS3 in CTMG
Linearization around AdS background
gµν = ḡµν + hµν
leads to linearized EOM that are third order PDE
1 (1)
G(1)
C = (DR DL DM h)µν = 0
µν +
µ µν
(1)
with three mutually commuting first order operators
¯α,
(DL/R )µ ν = δµν ± ` εµ αν ∇
(DM )µ ν = δµν +
Three linearly independent solutions to (1):
DL hL µν = 0 ,
DR hR µν = 0 ,
1 αν ¯
εµ ∇α
µ
D M hM
µν
=0
At chiral point left (L) and massive (M ) branches coincide!
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
25/42
Degeneracy at the chiral point
Will be quite important later!
Li, Song & Strominger found all solutions of linearized EOM.
I Primaries: L0 , L̄0 eigenstates ψ L/R/M with
L1 ψ R/L/M = L̄1 ψ R/L/M = 0
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
26/42
Degeneracy at the chiral point
Will be quite important later!
Li, Song & Strominger found all solutions of linearized EOM.
I Primaries: L0 , L̄0 eigenstates ψ L/R/M with
L1 ψ R/L/M = L̄1 ψ R/L/M = 0
I
Descendants: act with L−1 and L̄−1 on primaries
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
26/42
Degeneracy at the chiral point
Will be quite important later!
Li, Song & Strominger found all solutions of linearized EOM.
I Primaries: L0 , L̄0 eigenstates ψ L/R/M with
L1 ψ R/L/M = L̄1 ψ R/L/M = 0
I
I
Descendants: act with L−1 and L̄−1 on primaries
General solution: linear combination of ψ R/L/M
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
26/42
Degeneracy at the chiral point
Will be quite important later!
Li, Song & Strominger found all solutions of linearized EOM.
I Primaries: L0 , L̄0 eigenstates ψ L/R/M with
L1 ψ R/L/M = L̄1 ψ R/L/M = 0
I
I
I
Descendants: act with L−1 and L̄−1 on primaries
General solution: linear combination of ψ R/L/M
Linearized metric is then the real part of the wavefunction
hµν = Re ψµν
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
26/42
Degeneracy at the chiral point
Will be quite important later!
Li, Song & Strominger found all solutions of linearized EOM.
I Primaries: L0 , L̄0 eigenstates ψ L/R/M with
L1 ψ R/L/M = L̄1 ψ R/L/M = 0
I
I
I
Descendants: act with L−1 and L̄−1 on primaries
General solution: linear combination of ψ R/L/M
Linearized metric is then the real part of the wavefunction
hµν = Re ψµν
I
At chiral point: L and M branches degenerate. Get new solution
(DG & Johansson)
M (µ`) − ψ L
ψµν
µν
µ`→1
µ` − 1
new
ψµν
= lim
with property
DL ψ new
µν
= DM ψ new
D. Grumiller — Gravity in lower dimensions
µν
6= 0 ,
Which 3D theory?
(DL )2 ψ new
µν
=0
26/42
Sign oder nicht sign?
That is the question. Choosing between Skylla and Charybdis.
I
With signs defined as in this
talk: BHs positive energy,
gravitons negative energy
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
27/42
Sign oder nicht sign?
That is the question. Choosing between Skylla and Charybdis.
I
With signs defined as in this
talk: BHs positive energy,
gravitons negative energy
I
With signs as defined in
Deser-Jackiw-Templeton
paper: BHs negative energy,
gravitons positive energy
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
27/42
Sign oder nicht sign?
That is the question. Choosing between Skylla and Charybdis.
I
With signs defined as in this
talk: BHs positive energy,
gravitons negative energy
I
With signs as defined in
Deser-Jackiw-Templeton
paper: BHs negative energy,
gravitons positive energy
I
Either way need a mechanism to
eliminate unwanted negative
energy objects – either the
gravitons or the BHs
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
27/42
Sign oder nicht sign?
That is the question. Choosing between Skylla and Charybdis.
I
With signs defined as in this
talk: BHs positive energy,
gravitons negative energy
I
With signs as defined in
Deser-Jackiw-Templeton
paper: BHs negative energy,
gravitons positive energy
I
Either way need a mechanism to
eliminate unwanted negative
energy objects – either the
gravitons or the BHs
I
Even at chiral point the problem
persists because of the
logarithmic mode. See Figure.
Energy for all branches:
(Figure: thanks to N. Johansson)
D. Grumiller — Gravity in lower dimensions
Which 3D theory?
27/42
Outline
Why lower-dimensional gravity?
Which 2D theory?
Which 3D theory?
How to quantize 3D gravity?
What next?
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
28/42
Witten’s attempt
Different approach (without gravitons!):
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
29/42
Witten’s attempt
Different approach (without gravitons!):
I Naive remark 1: 3D gravity is trivial
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
29/42
Witten’s attempt
Different approach (without gravitons!):
I Naive remark 1: 3D gravity is trivial
I Naive remark 2: 3D gravity is non-renormalizable
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
29/42
Witten’s attempt
Different approach (without gravitons!):
I Naive remark 1: 3D gravity is trivial
I Naive remark 2: 3D gravity is non-renormalizable
I Synthesis of naive remarks: 3D quantum gravity may exist as
non-trivial theory
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
29/42
Witten’s attempt
Different approach (without gravitons!):
I Naive remark 1: 3D gravity is trivial
I Naive remark 2: 3D gravity is non-renormalizable
I Synthesis of naive remarks: 3D quantum gravity may exist as
non-trivial theory
I Positive cosmological constant: impossible?
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
29/42
Witten’s attempt
Different approach (without gravitons!):
I Naive remark 1: 3D gravity is trivial
I Naive remark 2: 3D gravity is non-renormalizable
I Synthesis of naive remarks: 3D quantum gravity may exist as
non-trivial theory
I Positive cosmological constant: impossible?
I Vanishing cosmological constant: S-matrix, but no gravitons!
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
29/42
Witten’s attempt
Different approach (without gravitons!):
I Naive remark 1: 3D gravity is trivial
I Naive remark 2: 3D gravity is non-renormalizable
I Synthesis of naive remarks: 3D quantum gravity may exist as
non-trivial theory
I Positive cosmological constant: impossible?
I Vanishing cosmological constant: S-matrix, but no gravitons!
I Therefore introduce negative cosmological constant
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
29/42
Witten’s attempt
Different approach (without gravitons!):
I Naive remark 1: 3D gravity is trivial
I Naive remark 2: 3D gravity is non-renormalizable
I Synthesis of naive remarks: 3D quantum gravity may exist as
non-trivial theory
I Positive cosmological constant: impossible?
I Vanishing cosmological constant: S-matrix, but no gravitons!
I Therefore introduce negative cosmological constant
I Define quantum gravity by its dual CFT at the AdS boundary
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
29/42
Witten’s attempt
Different approach (without gravitons!):
I Naive remark 1: 3D gravity is trivial
I Naive remark 2: 3D gravity is non-renormalizable
I Synthesis of naive remarks: 3D quantum gravity may exist as
non-trivial theory
I Positive cosmological constant: impossible?
I Vanishing cosmological constant: S-matrix, but no gravitons!
I Therefore introduce negative cosmological constant
I Define quantum gravity by its dual CFT at the AdS boundary
I Constructing this CFT still a “monstrous” effort...
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
29/42
Witten’s attempt
Different approach (without gravitons!):
I Naive remark 1: 3D gravity is trivial
I Naive remark 2: 3D gravity is non-renormalizable
I Synthesis of naive remarks: 3D quantum gravity may exist as
non-trivial theory
I Positive cosmological constant: impossible?
I Vanishing cosmological constant: S-matrix, but no gravitons!
I Therefore introduce negative cosmological constant
I Define quantum gravity by its dual CFT at the AdS boundary
I Constructing this CFT still a “monstrous” effort...
Maloney & Witten: taking into account all known contributions to path
integral leads to non-sensible result for partition function Z.
In particular, no holomorphic factorization:
ZMW 6= ZL · ZR
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
29/42
Witten’s attempt
Different approach (without gravitons!):
I Naive remark 1: 3D gravity is trivial
I Naive remark 2: 3D gravity is non-renormalizable
I Synthesis of naive remarks: 3D quantum gravity may exist as
non-trivial theory
I Positive cosmological constant: impossible?
I Vanishing cosmological constant: S-matrix, but no gravitons!
I Therefore introduce negative cosmological constant
I Define quantum gravity by its dual CFT at the AdS boundary
I Constructing this CFT still a “monstrous” effort...
Maloney & Witten: taking into account all known contributions to path
integral leads to non-sensible result for partition function Z.
In particular, no holomorphic factorization:
ZMW 6= ZL · ZR
Various suggestions to interpret this problem: need cosmic strings, need
sum over complex geometries, 3D quantum gravity does not exist by itself
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
29/42
Li, Song & Strominger attempt
Is CCTMG dual to a chiral CFT?
Interesting observations:
1. If left-moving sector is trivial, ZL = 1, then problem of holomorphic
factorization
Z = ZL · ZR = ZR
is solved.
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
30/42
Li, Song & Strominger attempt
Is CCTMG dual to a chiral CFT?
Interesting observations:
1. If left-moving sector is trivial, ZL = 1, then problem of holomorphic
factorization
Z = ZL · ZR = ZR
is solved.
2. CCTMG has
cL = 0
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
30/42
Li, Song & Strominger attempt
Is CCTMG dual to a chiral CFT?
Interesting observations:
1. If left-moving sector is trivial, ZL = 1, then problem of holomorphic
factorization
Z = ZL · ZR = ZR
is solved.
2. CCTMG has
cL = 0
3. Massive graviton degenerates with left boundary graviton: ψ M = ψ L
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
30/42
Li, Song & Strominger attempt
Is CCTMG dual to a chiral CFT?
Interesting observations:
1. If left-moving sector is trivial, ZL = 1, then problem of holomorphic
factorization
Z = ZL · ZR = ZR
is solved.
2. CCTMG has
cL = 0
3. Massive graviton degenerates with left boundary graviton: ψ M = ψ L
Thus, dual CFT chiral? If yes, we are done!
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
30/42
Li, Song & Strominger attempt
Is CCTMG dual to a chiral CFT?
Interesting observations:
1. If left-moving sector is trivial, ZL = 1, then problem of holomorphic
factorization
Z = ZL · ZR = ZR
is solved.
2. CCTMG has
cL = 0
3. Massive graviton degenerates with left boundary graviton: ψ M = ψ L
Thus, dual CFT chiral? If yes, we are done!
Suggestive to interpret LSS results as absence of gravitons
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
30/42
Li, Song & Strominger attempt
Is CCTMG dual to a chiral CFT?
Interesting observations:
1. If left-moving sector is trivial, ZL = 1, then problem of holomorphic
factorization
Z = ZL · ZR = ZR
is solved.
2. CCTMG has
cL = 0
3. Massive graviton degenerates with left boundary graviton: ψ M = ψ L
Thus, dual CFT chiral? If yes, we are done!
Suggestive to interpret LSS results as absence of gravitons
But:
Disagrees with results by Carlip, Deser, Waldron & Wise!
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
30/42
Gravitons in CCTMG
Is CCTMG dual to a logarithmic CFT?
New mode resolves apparent contradiction between LSS and CDWW.
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
31/42
Gravitons in CCTMG
Is CCTMG dual to a logarithmic CFT?
New mode resolves apparent contradiction between LSS and CDWW.
Interesting property:
L0
L̄0
ψ new
ψL
ψ new
ψL
D. Grumiller — Gravity in lower dimensions
=
=
2 12
0 2
0 12
0 0
ψ new
ψL
ψ new
ψL
How to quantize 3D gravity?
,
.
31/42
Gravitons in CCTMG
Is CCTMG dual to a logarithmic CFT?
New mode resolves apparent contradiction between LSS and CDWW.
Interesting property:
L0
L̄0
ψ new
ψL
ψ new
ψL
=
=
2 12
0 2
0 12
0 0
ψ new
ψL
ψ new
ψL
,
.
Such a Jordan form of L0 , L̄0 is defining property of a logarithmic CFT!
Note: called “logarithmic CFT” because some correlators take the form
hψ new (z)ψ new (0)i ∼ ln z + . . .
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
31/42
Gravitons in CCTMG
Is CCTMG dual to a logarithmic CFT?
New mode resolves apparent contradiction between LSS and CDWW.
Interesting property:
L0
L̄0
ψ new
ψL
ψ new
ψL
=
=
2 12
0 2
0 12
0 0
ψ new
ψL
ψ new
ψL
,
.
Such a Jordan form of L0 , L̄0 is defining property of a logarithmic CFT!
Note: called “logarithmic CFT” because some correlators take the form
hψ new (z)ψ new (0)i ∼ ln z + . . .
I
Logarithmic CFT: not unitary and not chiral!
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
31/42
Gravitons in CCTMG
Is CCTMG dual to a logarithmic CFT?
New mode resolves apparent contradiction between LSS and CDWW.
Interesting property:
L0
L̄0
ψ new
ψL
ψ new
ψL
=
=
2 12
0 2
0 12
0 0
ψ new
ψL
ψ new
ψL
,
.
Such a Jordan form of L0 , L̄0 is defining property of a logarithmic CFT!
Note: called “logarithmic CFT” because some correlators take the form
hψ new (z)ψ new (0)i ∼ ln z + . . .
I
Logarithmic CFT: not unitary and not chiral!
I
Either logarithmic or chiral CFT dual (or none)
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
31/42
Gravitons in CCTMG
Is CCTMG dual to a logarithmic CFT?
New mode resolves apparent contradiction between LSS and CDWW.
Interesting property:
L0
L̄0
ψ new
ψL
ψ new
ψL
=
=
2 12
0 2
0 12
0 0
ψ new
ψL
ψ new
ψL
,
.
Such a Jordan form of L0 , L̄0 is defining property of a logarithmic CFT!
Note: called “logarithmic CFT” because some correlators take the form
hψ new (z)ψ new (0)i ∼ ln z + . . .
I
Logarithmic CFT: not unitary and not chiral!
I
Either logarithmic or chiral CFT dual (or none)
I
Currently unknown which of these alternatives is realized!
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
31/42
Viability of the logarithmic mode, part 1
Explicit solution for logarithmic mode (DG & Johansson)
Is the logarithmic mode really there?
Collect in the following suggestions how the logarithmic mode could drop
out of the physical spectrum and show that none of them is realized.
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
32/42
Viability of the logarithmic mode, part 1
Explicit solution for logarithmic mode (DG & Johansson)
Is the logarithmic mode really there?
Collect in the following suggestions how the logarithmic mode could drop
out of the physical spectrum and show that none of them is realized.
Before starting, here is the explicit form of the

sinh
ρ
hnew
c τ − s ln cosh ρ 
µν =
cosh3ρ
logarithmic mode:

0 0 1
0 0 1 
1 1 0 µν


1
1
0
0 
− tanh2ρ s τ + c ln cosh ρ  1 1
0 0 −a2 µν
with
c = cos (2u) ,
D. Grumiller — Gravity in lower dimensions
s = sin (2u) ,
a=
(2)
1
sinh ρ cosh ρ
How to quantize 3D gravity?
32/42
Viability of the logarithmic mode, part 2
Physical mode with negative energy
Suggestion 1
The logarithmic mode is pure gauge?
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
33/42
Viability of the logarithmic mode, part 2
Physical mode with negative energy
Suggestion 1
The logarithmic mode is pure gauge? No!
hnew does not solve linearized Einstein equations. Thus is not pure gauge.
Note: confirmed by Sachs who considered logarithmic quasi-normal modes
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
33/42
Viability of the logarithmic mode, part 2
Physical mode with negative energy
Suggestion 1
The logarithmic mode is pure gauge? No!
hnew does not solve linearized Einstein equations. Thus is not pure gauge.
Note: confirmed by Sachs who considered logarithmic quasi-normal modes
Suggestion 2
Logarithmic mode has infinite energy and thus must be discarded?
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
33/42
Viability of the logarithmic mode, part 2
Physical mode with negative energy
Suggestion 1
The logarithmic mode is pure gauge? No!
hnew does not solve linearized Einstein equations. Thus is not pure gauge.
Note: confirmed by Sachs who considered logarithmic quasi-normal modes
Suggestion 2
Logarithmic mode has infinite energy and thus must be discarded? No!
E new = −
47
1152G `3
Energy is finite and negative.
Thus logarithmic mode leads to instability but cannot be discarded.
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
33/42
Viability of the logarithmic mode, part 3
Boundary conditions beyond Brown–Henneaux
Suggestion 3
New mode is not a small perturbation?
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
34/42
Viability of the logarithmic mode, part 3
Boundary conditions beyond Brown–Henneaux
Suggestion 3
New mode is not a small perturbation? It is!
hnew diverges asymptotically like ρ, but AdS background diverges
asymptotically like e2ρ . Thus hnew is really a small perturbation.
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
34/42
Viability of the logarithmic mode, part 3
Boundary conditions beyond Brown–Henneaux
Suggestion 3
New mode is not a small perturbation? It is!
hnew diverges asymptotically like ρ, but AdS background diverges
asymptotically like e2ρ . Thus hnew is really a small perturbation.
Suggestion 4
New mode is not asymptotically AdS?
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
34/42
Viability of the logarithmic mode, part 3
Boundary conditions beyond Brown–Henneaux
Suggestion 3
New mode is not a small perturbation? It is!
hnew diverges asymptotically like ρ, but AdS background diverges
asymptotically like e2ρ . Thus hnew is really a small perturbation.
Suggestion 4
New mode is not asymptotically AdS? It is!
Solution is asymptotically AdS
(0)
(1)
(0)
(2)
ds2 = dρ2 + γij e2ρ/` + γij ρ + γij + γij e−2ρ/` + . . . dxi dxj
(1) but violates Brown-Henneaux boundary conditions! (γij BH = 0)
Henneaux et al. showed precedents where this may happen in 3D
New boundary conditions replacing Brown-Henneaux (DG & Johansson)
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
34/42
Viability of the logarithmic mode, part 4
Brown–York boundary stress tensor
Suggestion 5
New mode leads to ill-defined Brown-York boundary stress tensor?
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
35/42
Viability of the logarithmic mode, part 4
Brown–York boundary stress tensor
Suggestion 5
New mode leads to ill-defined Brown-York boundary stress tensor? No!
Total action including boundary terms (Kraus & Larsen)
Z
√
1
1
Itotal = ICTMG +
d2 x −γ K −
8πG
`
Its first variation leads to Brown-York boundary stress-tensor:
Z
q
1
(0)
δItotal EOM =
d2 x −γ (0) T ij δγij
32πG
DG & Johansson: Tij is finite, traceless and chiral:
`
1 1
Tij = −
1 1 ij
16π G
Note: coincides with Brown-York boundary stress-tensor of global AdS3
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
35/42
Viability of the logarithmic mode, part 5
Artifact of linearization?
Suggestion 6
Maybe some non-linear “magic” kills the new mode?
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
36/42
Viability of the logarithmic mode, part 5
Artifact of linearization?
Suggestion 6
Maybe some non-linear “magic” kills the new mode? Unlikely!
DG, Jackiw & Johansson: classical phase space analysis of CCTMG
N=
1
1
2 × D − 2 × N1 − N2 =
2 × 18 − 2 × 14 − 6 = 1
2
2
N : number of physical degrees of freedom (per point)
D: number of canonical pairs in full phase space
I N1(2) : number of linearly independent first (second) class constraints
confirmed in more general calculation by Carlip
I
I
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
36/42
Viability of the logarithmic mode, part 5
Artifact of linearization?
Suggestion 6
Maybe some non-linear “magic” kills the new mode? Unlikely!
DG, Jackiw & Johansson: classical phase space analysis of CCTMG
N=
1
1
2 × D − 2 × N1 − N2 =
2 × 18 − 2 × 14 − 6 = 1
2
2
N : number of physical degrees of freedom (per point)
D: number of canonical pairs in full phase space
I N1(2) : number of linearly independent first (second) class constraints
confirmed in more general calculation by Carlip
I
I
I
Conclusion 1: logarithmic mode passed all tests so far
I
Conclusion 2: CCTMG is unstable; dual CFT probably logarithmic
D. Grumiller — Gravity in lower dimensions
How to quantize 3D gravity?
36/42
Outline
Why lower-dimensional gravity?
Which 2D theory?
Which 3D theory?
How to quantize 3D gravity?
What next?
D. Grumiller — Gravity in lower dimensions
What next?
37/42
Chiral vs. logarithmic
Pivotal open question: does dual CFT exist? is it chiral or logarithmic?
To Do
I
Chiral route: must show consistency of truncation!
I
Logarithmic: must show consistency of 2nd order perturbations!
D. Grumiller — Gravity in lower dimensions
What next?
38/42
Chiral vs. logarithmic
Pivotal open question: does dual CFT exist? is it chiral or logarithmic?
To Do
I
Chiral route: must show consistency of truncation!
I
Logarithmic: must show consistency of 2nd order perturbations!
ad chiral:
I restricting to Brown-Henneaux boundary conditions does not help
I Giribet, Kleban & Porrati showed that descendent of new mode
new
L̄−1 ψµν
= Yµν = Xµν + Lξ ḡµν
I
after a diffeomorphism ξ obeys Brown-Henneaux boundary conditions
Descendants of logarithmic mode are there even when boundary
conditions are restricted beyond requiring variational principle!
D. Grumiller — Gravity in lower dimensions
What next?
38/42
Chiral vs. logarithmic
Pivotal open question: does dual CFT exist? is it chiral or logarithmic?
To Do
I
Chiral route: must show consistency of truncation!
I
Logarithmic: must show consistency of 2nd order perturbations!
ad chiral:
I restricting to Brown-Henneaux boundary conditions does not help
I Giribet, Kleban & Porrati showed that descendent of new mode
new
L̄−1 ψµν
= Yµν = Xµν + Lξ ḡµν
I
I
after a diffeomorphism ξ obeys Brown-Henneaux boundary conditions
Descendants of logarithmic mode are there even when boundary
conditions are restricted beyond requiring variational principle!
Need different mechanism of truncation!
D. Grumiller — Gravity in lower dimensions
What next?
38/42
Chiral vs. logarithmic
Pivotal open question: does dual CFT exist? is it chiral or logarithmic?
To Do
I
Chiral route: must show consistency of truncation!
I
Logarithmic: must show consistency of 2nd order perturbations!
ad logarithmic:
I straightforward but somewhat lengthy calculation
I expand metric around AdS background up to second order:
(2)
gµν = ḡµν + hnew
µν + hµν
(2)
EOM lead to linear PDE for hµν :
2
D(3) h(2) = f (hnew
µν )
I
Check if h(2) really is smaller than hnew
µν
D. Grumiller — Gravity in lower dimensions
What next?
38/42
Chiral vs. logarithmic
Pivotal open question: does dual CFT exist? is it chiral or logarithmic?
To Do
I
Chiral route: must show consistency of truncation!
I
Logarithmic: must show consistency of 2nd order perturbations!
ad logarithmic:
I straightforward but somewhat lengthy calculation
I expand metric around AdS background up to second order:
(2)
gµν = ḡµν + hnew
µν + hµν
(2)
EOM lead to linear PDE for hµν :
2
D(3) h(2) = f (hnew
µν )
I
I
Check if h(2) really is smaller than hnew
µν
Might be rewarding exercise for a student
D. Grumiller — Gravity in lower dimensions
What next?
38/42
Which groundstate?
Two observations:
I Global AdS3 has mass and angular momentum in (C)CTMG
1
MAdS3 = µ JAdS3 = −
8G
D. Grumiller — Gravity in lower dimensions
What next?
39/42
Which groundstate?
Two observations:
I Global AdS3 has mass and angular momentum in (C)CTMG
1
MAdS3 = µ JAdS3 = −
8G
I If AdS3 is unstable in CCTMG because of logarithmic mode,
where does it run to?
D. Grumiller — Gravity in lower dimensions
What next?
39/42
Which groundstate?
Two observations:
I Global AdS3 has mass and angular momentum in (C)CTMG
1
MAdS3 = µ JAdS3 = −
8G
I If AdS3 is unstable in (C)CTMG because of massive graviton mode,
where does it run to?
Both observations suggest that there might be a ground state different
from pure AdS3 in (C)CTMG.
D. Grumiller — Gravity in lower dimensions
What next?
39/42
Which groundstate?
Two observations:
I Global AdS3 has mass and angular momentum in (C)CTMG
1
MAdS3 = µ JAdS3 = −
8G
I If AdS3 is unstable in (C)CTMG because of massive graviton mode,
where does it run to?
Both observations suggest that there might be a ground state different
from pure AdS3 in (C)CTMG.
Consider other possible ground states with less symmetry
D. Grumiller — Gravity in lower dimensions
What next?
39/42
Which groundstate?
Two observations:
I Global AdS3 has mass and angular momentum in (C)CTMG
1
MAdS3 = µ JAdS3 = −
8G
I If AdS3 is unstable in (C)CTMG because of massive graviton mode,
where does it run to?
Both observations suggest that there might be a ground state different
from pure AdS3 in (C)CTMG.
Consider other possible ground states with less symmetry
Example: warped AdS has four Killing vectors with U (1)L × SL(2, R)R
D. Grumiller — Gravity in lower dimensions
What next?
39/42
Which groundstate?
Two observations:
I Global AdS3 has mass and angular momentum in (C)CTMG
1
MAdS3 = µ JAdS3 = −
8G
I If AdS3 is unstable in (C)CTMG because of massive graviton mode,
where does it run to?
Both observations suggest that there might be a ground state different
from pure AdS3 in (C)CTMG.
Consider other possible ground states with less symmetry
Example: warped AdS has four Killing vectors with U (1)L × SL(2, R)R
Strominger et al.
:
Suggestive to consider warped AdS as possible groundstate of (C)CTMG
D. Grumiller — Gravity in lower dimensions
What next?
39/42
Most crucial question we would like to answer
Does 3D quantum gravity exist
with no strings attached?
D. Grumiller — Gravity in lower dimensions
What next?
40/42
Most crucial question we would like to answer
Does 3D quantum gravity exist
with no strings attached?
Perhaps a win-win situation!
I
Consider the possible outcomes to this question:
D. Grumiller — Gravity in lower dimensions
What next?
40/42
Most crucial question we would like to answer
Does 3D quantum gravity exist
with no strings attached?
Perhaps a win-win situation!
I
Consider the possible outcomes to this question:
I
If yes: we would have an interesting quantum theory of
gravity with BHs and gravitons to get conceptual
insight into quantum gravity
D. Grumiller — Gravity in lower dimensions
What next?
40/42
Most crucial question we would like to answer
Does 3D quantum gravity exist
with no strings attached?
Perhaps a win-win situation!
I
Consider the possible outcomes to this question:
I
If yes: we would have an interesting quantum theory of
gravity with BHs and gravitons to get conceptual
insight into quantum gravity
I
if no: potentially exciting news for string theory
D. Grumiller — Gravity in lower dimensions
What next?
40/42
Most crucial question we would like to answer
Does 3D quantum gravity exist
with no strings attached?
Perhaps a win-win situation!
I
Consider the possible outcomes to this question:
I
If yes: we would have an interesting quantum theory of
gravity with BHs and gravitons to get conceptual
insight into quantum gravity
I
if no: potentially exciting news for string theory
Thank you for your attention!
D. Grumiller — Gravity in lower dimensions
What next?
40/42
D. Grumiller — Gravity in lower dimensions
What next?
41/42
Some literature
D. Grumiller, W. Kummer, and D. Vassilevich, “Dilaton gravity in two
dimensions,” Phys. Rept. 369 (2002) 327–429, hep-th/0204253.
T. Hartman and A. Strominger, “Central charge for AdS2 quantum gravity,”
[arXiv:0803.3621 [hep-th]].
A. Castro, D. Grumiller, F. Larsen, and R. McNees, “Holographic Description
of AdS2 Black Holes,” [arXiv:0809.4264 [hep-th]].
W. Li, W. Song and A. Strominger, JHEP 0804 (2008) 082, 0801.4566.
S. Carlip, S. Deser, A. Waldron and D. Wise, Phys.Lett. B666 (2008) 272,
0807.0486, 0803.3998
D. Grumiller and N. Johansson, JHEP 0807 (2008) 134, 0805.2610.
G. Giribet, M. Kleban and M. Porrati, JHEP 0810 (2008) 045, 0807.4703.
D. Grumiller, R. Jackiw and N. Johansson, 0806.4185.
Thanks to Bob McNees for providing the LATEX beamerclass!
D. Grumiller — Gravity in lower dimensions
What next?
42/42