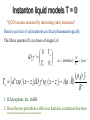Download Metal - CFIF

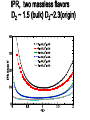
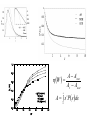
Role of Anderson-Mott localization in the
QCD phase transitions
Antonio M. García-García
[email protected]
Princeton University
ICTP, Trieste
We investigate in what situations Anderson localization may be relevant in the
context of QCD. At the chiral phase transition we provide compelling evidence
from lattice and phenomenological instanton liquid models that the QCD Dirac
operator undergoes a metal - insulator transition similar to the one observed in
a disordered conductor. This suggests that Anderson localization plays a
fundamental role in the chiral phase transition. Based on a recent relation
between the Polyakov loop and the spectral properties of the Dirac operator we
discuss how the confinement-deconfinement transition may be related to a
metal-insulator transition in the bulk of the spectrum of the Dirac operator.
James Osborn
In collaboration with
PRD,75 (2007) 034503 ,NPA, 770, 141 (2006) PRL 93 (2004) 132002
Outline
1. What is localization?
2. QCD vacuum as a conductor. QCD vacuum as a
disordered medium. Dyakonov - Petrov ideas.
3. Localization in lattice QCD.
4. A few words about QCD phase transitions.
5. Role of localization in the QCD phase transitions. Results
from instanton liquid models and lattice.
5.1 The chiral phase transition.
5.2 The deconfinement transition. In progress.
6. What’s next. Relation confinement and chiral symmetry
breaking. Quark diffusion in LHC.
What is localization?
Quantum particle in a random potential
Anderson-Mott localization
Quantum destructive interference, tunneling
or interactions can induce a transition
to an insulating state.
Insulator
For d < 3 or, at strong disorder,
in d > 3 all eigenstates are
localized in space.
Classical diffusion is
eventually stopped
Metal
d > 2, Weak disorder
Eigenstates delocalized.
Quantum effects do not alter
significantly the classical diffusion.
Insulator
Metal
How do we know that a metal is a metal?
Texbook answer: Look at the conductivity or other transport properties
Other options: Look at eigenvalue and eigenvectors

 D
QCD
 n  in  n
1. Eigenvector statistics:
Dq = d Metal
2. Eigenvalue statistics:
( q 1) d
Pq  L
H n  En n

Dq = 0 Insulator
2q
n
d
( q 1)( d  Dq )
(r ) d r ~ L
Dq = f(d,q) M-I transition
P( s)    s  i 1  i  /  
Level Spacing distribution:
i
Number variance:
 ( L  i   j / ) = n( L)  n( L)
2
Insulator  2 ( L)  L

( Poisson ) P( s)  e s
2
Metal   2 ( L) ~ log L

β  As2
( RMT ) Ps  ~ s e
2
QCD : The Theory of the strong interactions
High Energy g << 1 Perturbative
1. Asymptotic freedom
Quark+gluons, Well understood
Low Energy
g ~ 1 Lattice simulations
The world around us
2. Chiral symmetry breaking
 ~ (240MeV )
3
Massive constituent quark
3. Confinement
Colorless hadrons
V (r )  a / r  r
How to extract analytical information? Instantons , Monopoles, Vortices
QCD vacuum and instantons
tHooft, Polyakov, Shuryak, Diakonov, Petrov
Instantons (Polyakov,t'Hooft) : Non pertubative solutions of the classical
Yang Mills equation. Tunneling between classical vacua. Help
explain the chiral anomaly.
D =  μ  + gAμins 
Dψ0 r   0 ψ0 r  1/ r 3
Dirac operator has a zero mode in the field of an instanton
Spectral properties of the smallest eigenvalues of the Dirac operator
are controled by instantons Is that important? Yes.
 (m)
1
 ( )
1
   Tr ( D  m)   d
  lim 
mm0
V
m  i
V
Banks-Casher
(Kubo)
Spectral properties related to SBCS
Problem: Non linear equations
No superposition
Solution: Variational principles(Dyakonov,Petrov), Instanton liquid (Shuryak)
Fair agreement with lattice, phenomenology, no confinement
Instanton liquid models T = 0
"QCD vacuum saturated by interacting (anti) instantons"
Density and size of (a)instantons are fixed phenomenologically
The Dirac operator D, in a basis of single I,A:
Z
ILM
Nf
0
iD  
T
  de  det(D  m )
 SYM
k 1
  200MeV ,
T 

0

k
N
 1 fm
V
4
IA
AI
(I  A )
ˆ
TIA   d x ( x  z I )iD   A ( x  z A ) ~ i(u  R)
R3
4

I
1. ILM explains the chiSB

1 3N N 
   
  (240MeV )
  2 V 
3
1/ 2
c
3
2. Describe non perturbative effects in hadronic correlation
functions(Shuryak,Schaefer,Dyakonov,Petrov,Verbaarchot)
QCD vacuum as a conductor (T =0)
Metal
An electron initially bounded to a single atom gets delocalized due to
the overlapping with nearest neighbors.
QCD Vacuum
Zero modes initially bounded to an instanton get delocalized due to
the overlapping with the rest of zero modes. (Diakonov and Petrov)
Impurities
Instantons
Electron
Differences
Dis.Sys: Exponential decay
QCD vacuum Power law decay
Quarks
Nearest neighbors
Long range hopping!
QCD vacuum as a disordered conductor
Diakonov, Petrov, Verbaarschot, Osborn, Shuryak, Zahed,Janik
Instanton positions and color orientations vary
Impurities
T=0
Instantons
Electron
Quarks
long range hopping 1/Ra, a = 3<4
QCD vacuum is a conductor for any density of instantons
AGG and Osborn, PRL, 94 (2005) 244102
Localization in QCD
1. RMT and Thouless energy in QCD. Metallic limit of QCD, Verbaarschot,Osborn, PRL
Spectral correlations of the QCD Dirac
operator in the infrared limit are universal (Verbaarschot, Shuryak NPA 560 306 ,1993). and can be
obtained from a RMT with the symmetries of QCD
81 (1998) 268, Verbaarschot, Shuryak NPA 560 306 ,1993.
2
1
1
F
 L 
π
E
~
0
L
c

m
2
L
2. Localization in the QCD Dirac operator: C. Gattringer, M. Gockeler, et.al. Nucl. Phys.
B618, 205
(2001),R.V. Gavai, S. Gupta and R. Lacaze, Phys. Rev. D 65, 094504 (2002),M. Golterman and Y. Shamir, Phys. Rev. D 68,
074501 (2003). V. Weinberg, E.-M. Ilgenfritz, et.al, PoS { LAT2005}, 171 (2005), hep-lat 0705.0018, I. Horvath, N. Isgur, J.
McCune, and H. B. Thacker, Phys. Rev. D65, 014502 (2002), I. Horvath et al., Phys. Rev. D66, 034501 (2002), I. Horvath et al.,
Phys. Rev. D68, 114505 (2003)J. Greensite, S. Olejnik, M. Polikarpov, S. Syritsyn, and V. Zakharov, Phys. Rev. D71, 114507
(2005).
q( x)  TrF  F 
1   / 2 p ( x)

 

5
p 5    ( x) 5  ( x)
cut
“The general motivation behind the interest
issues like localization and (fractal) dimensionality was
the hope that the lowest modes are bound to certain singularities of the gauge field that in turn
would explain confinement. Here, “singular” is understood in a sense opposite to semiclassical
lumps, just in the spirit of Witten’s criticism of instantons.” hep-lat 0705.0018
1. Mobility edge at T = 0 in the infrared region of the spectrum (?).
2. Gauge configurations are multifractal with structures in three and lower
dimensions.
3. Instantons are irrelevant… is that true?
Phase transitions in QCD
At which temperature does the transition occur ? What is the nature of transition ?
Deconfinement:
Confining potential
vanishes.
L 0
Chiral
Restoration:Matter
becomes light.
Péter Petreczky
J. Phys. G30 (2004) S1259
 ~ 0
Quark- Gluon Plasma
perturbation theory only for
T>>Tc
Deconfinement and chiral restoration
They must be related but nobody* knows exactly how
Deconfinement: Confining potential vanishes. L 
Chiral Restoration:Matter becomes light.
0
 ~ 0
How to explain these transitions?
1. Effective model of QCD close to the phase transition (Wilczek,Pisarski):
Universality, epsilon expansion.... too simple?
2. QCD but only consider certain classical solutions (t'Hooft):
Instantons (chiral), Monopoles (confinement). Instanton do not dissapear at
the transiton (Shuryak,Schafer).
We propose that quantum interference and tunneling, namely, Anderson
localization plays an important role. Nuclear Physics A, 770, 141 (2006)
Localization and chiral transition: Why do we expect
a metal insulator transition close to the origin at finite
temperature?
1.The effective QCD coupling constant g(T) decreases as
temperature increases. The density of instantons also
decreases.
2. Zero modes are exponentially localized  ( R)  exp(TR )
in space but oscillatory in time.
3. Hopping amplitude restricted to T ~ exp( ATR)
IA
neighboring instantons.
4. Localization will depend strongly on the temperature. There
must exist a T = TLsuch that a metal insulator transition
takes place.
Dyakonov,
5. There must exist a T = Tc such that    0 Petrov
6. This general picture is valid beyond the instanton liquid
approximation (KvBLL solutions) provided that the hopping
induced by topological objects is short range.
Is TL = Tc ?...Yes
Does the MIT occur at the origin? Yes
Main Result
D =  + gA
QCD
μ
A  A , A
lat
At Tc
μ
ins

 D

QCD

 lim 
m  m0
  i 
n
n
 (m)
V

0
but also the low lying,



n
undergo a metal-insulator transition.
n
"A metal-insulator transition in the Dirac operator induces the
chiral phase transition "
Statistical analysis of spectra and eigenfunctions

 D
QCD
 n  in  n
1. Eigenvector statistics:
Dq = d Metal
( q 1) d
Pq  L
H n  En n

Dq = 0 Insulator
2q
n
d
( q 1)( d  Dq )
(r ) d r ~ L
Dq = f(d,q) M-I transition
2. Eigenvalue statistics:
P( s)    s  i 1  i  /  
Level Spacing distribution:
i
Number variance:
 ( L  i   j / ) = n( L)  n( L)
2
Insulator  2 ( L)  L

( Poisson ) P( s)  e s
2
2
Metal   2 ( L) ~ log L

β  As2
( RMT ) Ps  ~ s e
Signatures of a metal-insulator transition
1. Scale invariance of the spectral correlations.
A finite size scaling analysis is then carried
out to determine the transition point.
Skolovski, Shapiro, Altshuler
2.

P( s) ~ s
P(s) ~ e  As
s  1
2
 ( n) ~
s  1
var
n
3. Eigenstates are multifractals.
  (r ) d r ~ L
2q
d
 Dq ( q 1)
var  s 2  s
2
s n   s n P(s)ds
n
Mobility edge
Anderson transition
Spectrum is
scale invariant
ILM with 2+1 massless flavors,
P(s) of the lowest eigenvalues
We have observed a metal-insulator transition at T ~ 125 Mev
Metal insulator
transition
ILM, close to the origin, 2+1
flavors, N = 200
Level repulsion s << 1
Exponential decay s > 1
Unquenched ILM, 2 m = 0
ILM Nf=2 massless. Eigenfunction statistics
AGG and J. Osborn, 2006
Localization versus
chiral transition
Instanton liquid model Nf=2, masless
Chiral and localizzation transition occurs at the same temperature
Lattice QCD AGG, J. Osborn 2007
1. Simulations around the chiral phase transition T
2. Lowest 64 eigenvalues
Quenched
1. Improved gauge action
2. Fixed Polyakov loop in the “real” Z3 phase
Unquenched
1. MILC colaboration 2+1 flavor improved
2. mu= md = ms/10
3. Lattice sizes L3 X 4
Quenched Lattice QCD
IPR versus eigenvalue
Finite size
scaling analysis:
var  s  s
2+1 dynamical fermions
2
2
s   s P(s)ds
n
Quenched
n
Transiton from
metal to insulator
Quenched lattice, close to the origin
METAL
Inverse participation ratio versus T
Dynamical, 2+1
Quenched
For zero mass, transition sharper with the volume
First order
For finite mass, the condensate is volume independent
Crossover
Localization and order of the chiral phase transition
  
 lim 
m  m0
 ( m)
V
1. Metal insulator transition always occur close to the origin.
2. Systems with chiral symmetry the spectral density is sensitive to
localization.
3. For zero mass localization predicts a (first) phase transition not
crossover.
4. For a non zero mass m, eigenvalues up to m contribute to the
condensate but the metal insulator transition occurs close to the
origin only. Larger eigenvalue are delocalized so we expect a
crossover.
5. Multifractal dimension D2 should modify susceptibility exponents.
Confinement and spectral properties
Idea: Polyakov loop is expressed as the response of the Dirac operator to a
change in time boundary conditions Gattringer,PRL 97 (2006) 032003, hep-lat/0612020


U 4 ( x, N )  zU 4 ( x, N )


 2 N  ( x )  (1  z1 ) Nz1  ( x ) z1 

 z1

1  

L( x ) 

N
8 N   (1  z 2 )  z  ( x ) z

2
2



z
2


Politely Challenged in:
heplat/0703018,
Synatschke, Wipf,
Wozar


1 
N
N
N 
P  L( x ) 
2   (1  z1 ) z1  (1  z2 ) z2

8V  
z1
 z2






 ( x )   v  ( x, t )  v  ( x, t )
N
t 1
L,
R,
…. but sensitivity to spatial boundary conditions
is a criterium (Thouless) for localization!
Localization and confinement
The dimensionless conductance, g, a measure of localization, is related to
the sensitivity of eigenstates to a change in boundary conditions.
1.What part of the spectrum contributes the most to the
Polyakov loop?.Does it scale with volume?
2. Does it depend on temperature?
3. Is this region related to a metal-insulator transition at Tc?
4. What is the estimation of the P from localization theory?
5. Can we define an order parameter for the chiral phase
transition in terms of the sensitivity of the Dirac operator to
a change in spatial boundary conditions?
Accumulated Polyakov loop versus eigenvalue
Confinement is controlled by the ultraviolet part of the spectrum
P

Localization and Confinement
IPR (red), Accumulated Polyakov loop (blue) for T>Tc as a
function of the eigenvalue.
Metal
prediction
MI
transition?
Conclusions
●
●
●
Eigenvectors of the QCD Dirac operator becomes more
localized as the temperature is increased.
For a specific temperature we have observed a metalinsulator transition in the QCD Dirac operator.
For lattice and ILM, and for quenched and unquenched we
have found two transitions close to the origin and in the UV
part of the spectrum and.
MAIN
"The Anderson transition occurs at the same T than the chiral
phase transition and in the same spectral region“
Wish
“ Confinement-Deconfinemente transition has to do with
localization-delocalization in time direction”
What's next?
1. How critical exponents are affected by
localization?
2. Confinement and localization, analytical
result?
3. How are transport coefficients in the quark
gluon plasma affected by localization?
4. Localization and finite density. Color
superconductivity.
Quenched ILM, IPR, N = 2000
Metal
IPR X N= 1
Insulator
IPR X N = N
Multifractal
Similar to overlap prediction
Origin
Morozov,Ilgenfritz,Weinberg, et.al.
Bulk
IPR X N =
D2~2.3(origin)
N
D2
Quenched ILM, Origin, N = 2000
For T < 100 MeV we expect (finite size scaling) to
see a (slow) convergence to RMT results.
T = 100-140, the metal insulator transition occurs
IPR, two massless flavors
D2 ~ 1.5 (bulk) D2~2.3(origin)
A A
 W  =
A A
RMT
P
RMT
A =  s Ps ds

2
0
How to get information from a bunch of levels
Spectrum
Unfolding
Spectral Correlators
Quenched ILM, Bulk, T=200
Nuclear (quark) matter at finite temperature
1. Cosmology 10-6 sec after Bing Bang, neutron stars (astro)
3 Analytical, 4N=4 super YM ?
2. 1
Lattice QCD finite2size effects.
3. High energy Heavy Ion Collisions. RHIC, LHC
Colliding Nuclei
Hard
Collisions
QG Plasma ?
Hadron Gas &
Freeze-out
sNN = 130, 200 GeV
(center-of-mass energy per nucleon-nucleon collision)
Multifractality
Intuitive: Points in which the modulus of the
wave function is bigger than a (small) cutoff M. If
the fractal dimension depends on the cutoff M,
Kravtsov, Chalker,Aoki,
the wave function is multifractal.
Schreiber,Castellani
IPR  I =  ψ r  d r  L
4
2
Ld
n
d
 D2
Instanton liquid models T = 0
"QCD vacuum saturated by interacting (anti) instantons"
Density and size of (a)instantons are fixed phenomenologically
The Dirac operator D, in a basis of single I,A:
0
iD  
T
T 

0

IA
AI
  200MeV ,
N
 1 fm
V
4
(


)
T   d x ( x  z )iD  ( x  z ) ~ i(u  Rˆ )
R
4
IA


I
I
I
A
A
3
A
4
1. ILM explains the chiSB
2. Describe non perturbative effects in hadronic correlation functions
(Shuryak,Schaefer,dyakonov,petrov,verbaarchot)
QCD Chiral Symmetries
L,R  (1   5 )
Classical
SU A (3)  SUV (3)  UV (1)  U A (1)

Quantum
SUV (3)  UV (1)
U(1)A explicitly broken by the anomaly.
SU(3)A spontaneously broken by the QCD vacuum
qq  (250 MeV )
3
Dynamical mass
Eight light Bosons (,K,), no parity doublets.
Quenched lattice QCD simulations
Symanzik 1-loop glue with asqtad valence
3. Spectral characterization:
Spectral correlations in a metal are given by random
matrix theory up to the Thouless energy Ec. Matrix
elements are only constrained by symmetry
2
2
Metal 
n ( E ) = n  n ~ log E

β  As 2
( RMT ) 


P
s
~
s
e

2
Ec  1 / L
2
In units of the mean level spacing,
the Thouless energy,
g
Ec

d 2
L
Eigenvalues in an insulator are not correlated.
Insulator n ( E )  E

( Poisson )  P( s)  e s
2
In the context of QCD the metallic
region corresponds with the infrared
limit (constant fields) of the Dirac
operator" (Verbaarschot,Shuryak)
1. QCD, random matrix theory, Thouless energy:
Spectral correlations of the QCD Dirac operator in the infrared limit are
universal (Verbaarschot, Shuryak Nuclear Physics A 560 306 ,1993). They can be
obtained from a RMT with the symmetries of QCD.
1. The microscopic spectral density is universal, it depends only on the
global symmetries of QCD, and can be computed from random matrix
theory.
2
2

 (s) ~ s J 0 (s)  J1 (s)

2. RMT describes the eigenvalue correlations of the full QCD Dirac
operator up to Ec. This is a finite size effect. In the thermodynamic
limit the spectral window in which RMT applies vanishes but at the
same time the number of eigenvalues, g, described by RMT diverges.
Fπ2
Ec ~ 2  0
L
L
Ec
g  ~ Fπ2 L2  

L
Quenched ILM, T =200, bulk
Mobility edge in the Dirac
operator. For T =200 the
transition occurs around the
center of the spectrum
D2~1.5 similar to the
3D Anderson model.
Not related to chiral
symmetry