Download Dividing Real Numbers

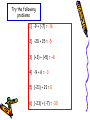
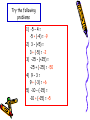
Real Numbers
Rational and Irrational
Let’s look at the relationships between
number sets. Notice rational and irrational
numbers make up the larger number set
known as Real Numbers
A number represents the value or quantity of
something… Like how much money you have.. Or
how many marbles you have… Or how tall you
are.
As you may remember from earlier grades
there are different types of numbers.
Rational Numbers
Fractions are rational numbers in
disguise
Rational number – the set of all numbers that
can be written in the form of a/b, where a and
b are integers and b ≠ 0.
Because a fraction can be written as a decimal, any
rational number a/b can be written in decimal
form.
When you divide the denominator of a fraction into
the numerator, the result is either a terminating
or repeating decimal.
A terminating decimal has a finite number of
nonzero digits to the right of the decimal
point, such as 0.25 or 0.10.
A repeating decimal has a string of one or more
digits that repeat infinitely, such as 1.555555…,
or 0.345634563456… These repeating decimals
can be indicated by a bar over the repeating
digits, 1.5 or 0.3456
Write 0.375 as a fraction in simplest form.
0.375
375/1000 = 3/8, so 0.375 = 3/8
Write 1/3 as a decimal.
Divide 1 by 3 and you will see how the process
will repeat infinitely.
0.333333333333
A number line - is an infinitely long line whose
points match up with the real number system.
Here are the rational numbers represented on
a number line.
Integers
The coldest temperature on record in
the U.S. is -80° F, recorded in 1971 in
Alaska
Integers are used to represent real-world
quantities such as temperatures, miles per
hour, making withdrawals from your bank
account, and other quantities. When you know
how to perform operations with integers, you
can solve equations and problems involving
integers.
By using integers, you can express elevations
above, below, and at sea level. Sea level has
an elevation of 0 feet. Badwater Basin in Utah
is -282 below sea level, and Clingman’s Dome
in the Great Smokey Mountains is +6,643
above sea level.
If you remember, the whole numbers are the
counting numbers and zero:
0, 1, 2, 3,…
Integers - the set of all whole numbers and
their opposites. This means all the positive
integers and all the negative integers
together.
Opposites – two numbers that are equal
distance from zero on a number line; also
called additive inverse.
The additive inverse property states that if
you add two opposites together their sum is 0
-3 + 3 = 0
Integers increase in value as you move to the
right along a number line. They decrease in value
as you move to the left. Remember to order
numbers we use the symbol < means “less than,”
and the symbol > means “is greater than.”
A number’s absolute value - is it’s distance from
0 on a number line. Since distance can never be
negative, absolute values are always positive.
The symbol || represents the absolute value of a
number. This symbol is read as “the absolute
value of.” For example |-3| = 3.
Finding absolute value using a number line is
very simple. You just need to know the
distance the number is from zero. |5| = 5,
|-6| = 6
Lesson Quiz
Compare, Use <, >, or =.
5) The coldest
1) -32 □ 32
temperature ever
2) 26 □ |-26|
recorded east of the
Mississippi is fifty3) -8 □ -12
four degrees below
4) Graph the numbers -2, 3,
zero in Danbury,
-4, 5. and -1 on a number
Wisconsin, on January
line. Then list the
24, 1922. Write the
numbers in order from
temperature as an
least to greatest.
integer.
Integer Operations
Rules for Integer Operations
Adding Integers
When we add numbers with the same signs,
1) add the absolute values, and
2) write the sum (the answer) with the sign of the
numbers.
When you add numbers with different signs,
1) subtract the absolute values, and
2) write the difference (the answer) with the sign of
the number having the larger absolute value.
Try the following
problems
1) -9 + (-7) = -16
2) -20 + 15 = -5
3) (+3) + (+5) = +8
4) -9 + 6 = -3
5) (-21) + 21 = 0
6) (-23) + (-7) = -30
Subtracting Integers
You subtract integers by adding its opposite.
9 – (-3)
9 + (+3) = +12
-7 – (-5)
-7 + (+5) = -2
Try the following
problems
1) -5 – 4 =
-5 + (-4) = -9
2) 3 – (+5) =
3 + (-5) = -2
3) -25 – (+25) =
-25 + (-25) = -50
4) 9 – 3 =
9 + (-3) = +6
5) -10 – (-15) =
-10 + (+15) = +5
Adding and Subtracting Real Numbers
When there is a negative sign in front of an expression
in parentheses, such as –(3 + 4), there are two methods
that you can use to simplify the expression.
The first method is to simplify within the parentheses
and then apply the rule for the addition of opposite
signs as shown here.
Simplify 10 –(-5 + 3)
10 –(-5 + 3) = 10 – (-2)
= 10 + 2
= 12
Work within parentheses. Add -5 and 3 to get -2.
Write subtraction as addition.
A second method that can be used to simplify –(3 + 4)
is based on the (Multiplicative Property of -1)
For all real numbers a, -1(a) = -a, or the opposite of a.
This property can be extended to more than one
term with the parentheses.
The Opposite of a Sum -(a + b) = -a – b
The Opposite of a Difference -(a – b) = -a + b = b – a
Simplify –(- 3 + 5)
-1(-3 + 5) = 3 – 5
= -2
Try the following
problems
1)
2)
3)
4)
5)
6)
-12 – (4 + 9)
-(2x + 3)
-(3 + 4) – (5 + 6)
-(x + 7)
-(3 + 4) – (5 + 6) + (2 – 5)
-[(-2 – 8) – (-5 + 11)] – [(1 – 10) –(-3-3)]
Multiplying and Dividing Integers
If the signs are the same,
the answer is positive.
If the signs are different,
the answer is negative.
Try the following
problems
Think of multiplication as repeated addition.
3 · 2 = 2 + 2 + 2 = 6 and 3 · (-2) = (-2) + (-2) + (-2) = -6
1) 3 · (-3) = Remember multiplication is fast adding
= 3 · (-3) = (-3) + (-3) + (-3) = -9
2) -4 · 2 = Remember multiplication is fast adding
= -4 · 2 = (-4) + (-4) = -8
Multiply the following
 3  2 
    
 5  3 
2
 3
4 
 5
 12 6 5
Dividing Integers
Multiplication and division are inverse operations. They “undo”
each other. You can use this fact to discover the rules for
division of integers.
4 · (-2) = -8
-8 ÷ (-2) = 4
same sign positive
-4 · (-2) = 8
8 ÷ (-2) = -4
different signs
negative
The rule for division is like the rule for multiplication.
Try the following
problems
1) 72 ÷ (-9)
72 ÷ (-9)
-8
Think: 72 ÷ 9 = 8
The signs are different, so the quotient is negative.
2) -144 ÷ 12
-144 ÷ 12 Think: 144 ∕12 = 12
-12
The signs are different, so the quotient is negative.
3) -100 ÷ (-5)
-100 ÷ (-5)
Think: 100 ÷ 5 = 20
The signs are the same, so the quotient is positive.
Divide the following
3

5
3

2
3
 3 
4   4 
5
 5 
 1.2   1.2
Lesson Quiz
Find the sum or difference
Find the product or quotient
1) -7 + (-6) =
2) -15 + 24 + (-9) =
Evaluate x + y for x = -2
and y = -15
3) 3 – 9 =
4) -3 – (-5) =
Evaluate x – y + z for
x = -4, y = 5, and z = -10
1)
2)
3)
4)
5)
-8 · 12 =
-3 · 5 · (-2) =
-75 ÷ 5 =
-110 ÷ (-2) =
The temperature in Bar
Harbor, Maine, was -3 F.
During the night, it
dropped to be four times
as cold. What was the
temperature then?
Dividing Real Numbers
Because you can multiply any two real numbers,
and every nonzero real number has a
multiplicative inverse, you can define division
using multiplication and multiplicative inverse.
Example 1
Try This
1
2
1
5
Using Multiplication and division with other operations
You have learned the order of operations and the rules
for adding subtracting, multiplying, and dividing real
numbers. You can now simplify many expressions that
involve positive and negative numbers.
Simplify
Another
Simplify
1
-5
3
4
Try This
The Distributive Property and Combining Like
Terms
A monomial - is a real number or the product
of a real number and a variable raised to a
whole-number power.
For example, 6, -4c, and 3x2
are monomials.
When there is both a number and a variable in
the product, the number is called the
coefficient. In the monomials -4c and 3x2, -4
and 3 are coefficients.
• Recall that a monomial with no visible coefficient,
such as x, actually has a coefficient of 1.
Similarly, -x has a coefficient of -1.
Using the Distributive
Property
Simplify
Example 1
Example 2
Example 3
Try This
Simplify
More Distributive
Property
When you have unlike terms in a sum or
difference within parentheses, you may have
to use the opposite of a sum or a difference
when simplifying.
Simplify
Example 1
Try This
Using the Distributive Property to multiply and divide
You can use the Distributive Property to simplify a
product. The Distributive Property applies to both
positive and negative numbers.
Example 1
Simplify
Example 2
More
Example 3
Next Example
Example 4
Try This
Try This
Rational Numbers
Fractions and Decimals
Rational numbers, numbers that can be
written in the form a/b (fractions), with
integers for numerators and denominators.
Integers and certain decimals are rational
numbers because they can be written as
fractions.
b
1
2
3
4
5
…
a
1
2
3
4
5
…
1/1
1/2
1/3
1/4
1/5
2/1
2/2
2/3
2/4
2/5
3/1
3/2
3/3
3/4
3/3
4/1
4/2
4/3
4/4
4/5
5/1
5/2
5/3
5/4
5/5
…
…
…
…
…
Hint: When given a rational number in decimal
form (such as 2.3456) and asked to write it as a
fraction, it is often helpful to “say” the decimal
out loud using the place values to help form the
fraction.
2
o
n
e
s
.
a
n
d
3
t
e
n
t
h
s
4
h
u
n
d
r
e
d
T
h
s
5
t
h
o
u
s
a
n
d
t
h
s
6
tent
h
o
u
s
a
n
d
t
h
s
Write each rational number as
a fraction:
Rational number
In decimal form
0.3
0.007
-5.9
Rational number
In fractional form
3/10
7/1000
-59/10
Hint: When checking to see which fraction is
larger, change the fractions to decimals by
dividing and comparing their decimal values.
Which of the given numbers
is greater?
2/3 and 1/4
-7/3 and – 11/3
Using full calculator display to
compare the numbers
.6666666667
-2.333333333
> .25
> -3.666666667
Examples of rational numbers are:
6 or 6/1
-2 or -2/1
½
-5/4
2/3
2/3
21/55
53/83
can also be written as
can also be written as
can also be written as
can also be written as
can also be written as
can also be written as
can also be written as
can also be written as
6.0
-2.0
0.5
-1.25
.66
0.666666…
0.38181818…
0.62855421687…
the decimals will repeat after 41 digits
Examples: Write each rational number as a
fraction:
1)
0.3
2)
0.007
3)
-5.9
4)
0.45
Since Real Numbers are
both rational and
irrational , ordering them
on a number line can be
difficult if you don’t pay
attention to the details.
As you can see from the
example at the left,
there are rational and
irrational numbers placed
at the appropriate
location on the number
line.
This is called ordering
real numbers.
Irrational numbers
√2 = 1.414213562…
no perfect squares here
Irrational number – a number that cannot be
expressed as a ratio of two integers or as a
repeating or terminating decimal.
• An irrational number cannot be expressed as a
fraction.
• Irrational numbers cannot be represented as
terminating or repeating decimals.
• Irrational numbers are non-terminating, nonrepeating decimals.
Examples of irrational
numbers are:
 = 3.141592654…
√2 = 1.414213562…
0.12122122212
√7, √5, √3, √11,
343√
Non-perfect squares
are irrational
numbers
Note:
The √ of perfect
squares are rational
numbers.
√25 = 5
√16 = 4
√81 = 9
Remember: Rational numbers when divided will
produce terminating or repeating decimals.
NOTE:
Many students think that 
is a terminating decimal,
3.14, but it is not. Yes,
certain math problems ask
you to use  as 3.14, but
that problem is rounding
the value of
to make
your calculations easier.
It is actually an infinite
decimal and is an irrational
number.

There are many numbers
on a real number line
that are not rational.
The number is not a
rational number, and it
can be located on a real
number line by using
geometry. The number
is not equal to 22/7,
which is only an
approximation of the
value. The number
is exactly equal to the
ratio of the
circumference of a circle
to its diameter.



ENJOY
YOUR PI
π