Download LOC10a Kirchoff`s Laws

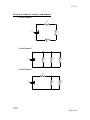
6/27/17
Kirchhoff’s Laws
Equipment Needed
AC/DC Electronics Laboratory,
Pasco EM-8656
Power Supply, Fisher-EMD S44175-1
Battery Eliminator
Lead, Alligator Clip
Resistor, 100Ω
Lead, Banana/Alligator
Resistor, 330 Ω,
Lead, Banana/Banana
Resistor, 560Ω
Multi-Meter, Digital (2)
Introduction
In this lab we will explore the consequences of Kirchhoff’s Laws for electric
circuits for the case of three circuits. Our approach will be to predict every
quantity we can, and then measure that quantity. Then we will compare the
measured and predicted values.
Kirchoff’s Laws provide tools with which we can analyze complicated circuits.
With the benefit of hindsight, we realize that they are equivalent to statements of
conservation of energy and charge. Kirchhoff’s Current Law is illustrated in
Figure 1. It states that the algebraic sum of the current at a junction point (a node)
is zero. This means that the total current flowing into a point equals the total
current flowing out. In Figure 1, Kirchhoff’s Current Law would be expressed
where
is the current. We can understand the equivalence of
Kirchhoff’s Current Law to the law of conservation of charge with the following
heuristic argument. Imagine that the current entering the node was less than that
exiting it. Since current is the rate of flow of charge, this would mean that more
charge was leaving the node than entering it. Thus charge would have to be
created at the node, violating conservation of charge. In order for the node to not
act as a source (or a sink for that matter) of charge, Kirchhoff’s Current Law must
hold.
NRG 2426
478158581
Page 1 of 6
6/27/17
This can be demonstrated:
Figure 1: Since
is coming into the node it is a positive quantity.
and
are leaving the node, so they are negative. Thus, Kirchoff’s
Current Law yields
I1
or
.
I2
I3
Figure 2 illustrates Kirchhoff’s Voltage Law. It states that the algebraic sums of
the potential differences around a closed loop is zero. Put another way, the sum
of the potential gains equals the sum of the potential drops. For the circuit shown
in Figure 2 where
is the emf and
is the resistance, Kirchhoff’s Voltage Law
yields E1  IR1  E2  IR2  0 , or equivalently E1  E2  IR1  IR2 . We can see
the equivalence of Kirchhoff’s Current Law to conservation of energy by
following a charge Q around the loop. Since the electric force is a conservative
force, if the charge makes a complete trip around the loop it must end up with a
net change in energy of U  0 . Adding up the energy gains we obtain,
QE1  QE 2 . Adding up the energy losses we obtain QIR1  QIR 2 . The net
change in energy around the loop is
. If we simply divide by Q, we obtain
Kirchhoff’s Voltage Law.
Figure 2
Kirchhoff’s Voltage Law applied to a single loop yields
E1  IR1  E2  IR2  0
NRG 2426
478158581
Page 2 of 6
6/27/17
R1
E1
E2
R2
The arrows in the center of the ring indicate Current flow.
We will now examine how these laws apply to some real circuits.
Procedure
We will examine three circuits, which we will construct by connecting the three
resistors on the circuit board in different ways. First, before making any
connections, use the DMM to measure the value of each of the resistors. It is
important know the identity of each resistor before wiring into the circuit. Record
the values as
,
, and
. The measured values are the ones you will use in
your calculations.
Resistors
Nominal Value
Measured Value
100Ω
330Ω
560Ω
Battery Eliminator
6VDC
For each of the following circuits, do the following (show your work):
1. Calculate the equivalent resistance using the measured values of the resistors.
2. Measure the equivalent resistance
3. Calculate the predicted current through each resistor using the measured values of
the resistors and the measured value of the battery eliminator.
4. Measure the current through each resister.
5. Calculate the predicted potential difference across each resistor using the
measured value of the battery eliminator.
6. Measure the potential difference across each resistor.
NRG 2426
478158581
Page 3 of 6
6/27/17
Here are a few pointers to help you accomplish these objectives:
1. The equivalent resistance is measured by simply measuring with the DMM across
the network. Always measure resistance with the resistors NOT connected to the
power supply. If the resistors are connected to the power supply, then capacitance
and resistance in the power supply as well as current flowing in the circuit can
greatly skew your readings. The leads must be plugged into the Ω and the COM
plug respectively. For measuring resistance the meter dial should be set in the
2kΩ range.
2. The potential difference across an element can always be measured by placing the
probes of the DMM across the two sides of the element. The leads must be
plugged into the V plug and the COM plug respectively. For measuring potential
difference the meter dial should be set in the 20VDC range. Note: For calculated
values use the measured potential at the battery eliminator.
3. A conventional ammeter must ALWAYS be placed in series with the element
through which you wish to measure the current. The leads must be plugged into
the 200mA plug and the COM plug. For measuring amperage the meter dial
should in the 200mADC range. Unlike the voltage measurement the ammeter
will have to be moved and inserted into the circuit specific to each leg to be
measured. If you have trouble with this your instructor or lab tech can help. If
you’re not sure, do not turn on the circuit until it is checked.
4. We will use the battery eliminator set at the nominal voltage 6VDC. Be sure to
measure the actual voltage.
NRG 2426
478158581
Page 4 of 6
6/27/17
Circuits to construct, analyze, and measure
Circuit Number 1
R1
V
R2
R3
Circuit Number 2
V
R1
R2
R3
R2
R3
Circuit Number 3
R1
V
NRG 2426
478158581
Page 5 of 6
6/27/17
Report Format
Your report should consist of three pages, with one page corresponding to each of
the circuits. Each page should include a schematic of the circuit and a very neat
and clear theoretical analysis of the circuit. In a table you should list your
calculated values and your measured values.
Note: Include a column for percent error calculated between theoretical and
experimental. What are some sources of any systematic error?
NRG 2426
478158581
Page 6 of 6