Download Effects of curing pressure on Mode II fracture toughness of uni

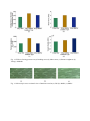
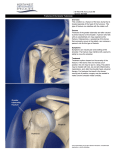
Effects of curing pressure on Mode II fracture toughness of uni-directional
GFRP laminates
S. Sajitha, V. Arumugama, H.N.Dhakalb*
a
b
Department of Aerospace Engineering, MIT Campus, Anna University, Chennai, India
Advanced Polymer and Composites Research Group, School of Engineering, University of
Portsmouth, PO1, 3DJ, UK.
ABSTRACT
The purpose of this work is to investigate the effect of curing pressure on the Mode II
interlaminar fracture toughness behavior of uni-directional glass fibre reinforced plastics
(GFRP). Investigation was carried out experimentally on uni-directional GFRP specimens
using end notched flexure (ENF) tests to find out the changes in the material and geometric
properties due to the application of pressure. Stiffness of the different laminates cured under
different pressure were studied and it was shown that both material and geometric stiffness
accounts for the total stiffness of the laminate, but their contribution to total stiffness varies.
It is shown that fracture toughness values, GIIC , remain unaffected by stiffness since it is only
related to the new surfaces created due to crack initiation and propagation. It is shown that
the thickness of the matrix layer influences all the properties, including the fracture
toughness. The laminates cured at 5 Psi, 400 Psi and 800 Psi exhibit different fracture
toughness. Optimum thickness of matrix layer offers both adhesive and cohesive resistance to
the crack propagation and thus offers high fracture resistance.
Keywords: Glass fibres reinforced plastics, End Notch Flexure, Mode II fracture toughness,
Delamination.
* Corresponding author. Tel: + 44 (0) 23 9284 2582; fax: + 44 (0) 23 9284 2351.
E-mail: [email protected]
1. Introduction
Glass and carbon fibre reinforced composite materials are increasingly used in aerospace and
automotive applications due to their high strength to weight ratio and high modulus compared
to their metal counterparts. In spite of being very stiff, laminated composite structures are
susceptible to delamination. Delamination is always associated with the initiation and
propagation of an interlaminar crack. Delamination creates new surfaces with the expense of
the strain energy released. Standard methods are required for specimen preparation and
testing for measurement of strain energy released during initiation and progression of
interlaminar cracking [1]. The fracture behavior and the mode of failure involved in Mode II
delamination of end notched flexure (ENF) specimens have been discussed [2-4]. Stevanovic
et al. showed that pre-crack conditions have no influence on the fracture toughness of the
composite under Mode II loading [5]. Li et al. found that GIIIc corresponding to onset of crack
propagation substantially increased with decreasing fiber volume fraction due to the increased
matrix volume allowing increased plastic deformation energy dissipation in the matrix resin
prior to macroscopic crack propagation [6]. Ramazan Kahraman at al. showed that adhesion
strength decreases as the thickness of the adhesive increases due to high stress generated in
the adhesive so that cohesive failure of adhesive was observed [7]. Ireman et al. explained
that the brittle epoxy system has considerably lower delamination toughness than the
materials with toughened epoxy resins. He also investigated and found that thinner pre-crack
film produces lower values of the initial delamination fracture toughness. Matrix cracks and
the interface in which the initial defect is located play an important role in the growth
behaviour [8]. An algorithm to predict the path of cracks developed from pre-existing cracks
in highly heterogeneous material was created [9]. A new criterion on Mode II fracture was
proposed which suggest that the mode II crack initiation is controlled by the distortional
strain energy density factor [10]. The effect of delamination size and shape on buckling
behaviour was investigated using circular and elliptical delamination [11]. The effect of notch
angle, bonding strength and the loading point locations on the crack initiation load was
studied [12]. Hansang et al. revealed the influence of adhesive strength on Mode I fracture
toughness of the hierarchical composites [13].
The effects of adhesive strength between inclusion and matrix and eccentricity of the
inclusion from the crack path near crack-tip have been examined. If bonding is weak the
dynamically growing Mode I crack is attracted and trapped momentarily, whereas it is
deflected away if the inclusion is bonded strongly to the matrix [14]. The effect of nano
particles on Mode I and Mode II fracture response of composite laminates were studied [1516]. Effect of fibre properties, fibre diameter and modulus, on fracture toughness was
investigated. Decrease in fiber diameterleads to drop in the fracture toughness due to the
transition of the failure mode from fiber pull-out to fiber breakage. Decrease in delamination
resistance is noted under Mode I and Mixed mode loading as fibre modulus increases due to
the modification in interlaminar layer geometry and crack propagation within the fibres [1718]. Ducept et al. compared laminated composites and adhesive joined composites and found
that crack propagation was unstable in adhesively bonded composites under Mode I loading
but stable under Mode II loads, which is due to cohesive failures. Also, fracture energies are
much higher for the bonded ones than for the laminated composite [19]. Influence of shape of
particle in particulate composite was studied and it was shown that toughness was improved
by spherical particles but not plate-like nanoclay particles [20]. Yasuhide Shindo et al.
revealed that the delamination growth rate is lower at low temperatures due to decrease in the
hackle spacing with decreasing temperature [21]. Lyashenko et al. evaluated fracture
toughness values based on Euler Bernoulli beam theory formula for different fracture
mechanisms of adhesive fracture and cohesive fracture, and showed that higher fracture
resistance is evident for rougher surface. This is indicative of cohesive fracture whereas a
surface with exposed fibers is typical of adhesive fracture [22]. Baere et al. [23] studied the
Mode I and Mode II interlaminar fracture toughness behaviour of a carbon fabric reinforced
thermoplastic and concluded that, for mode I fracture toughness, the crack was unstable,
whereas for mode II ENF testing the crack was stable. They suggested that a higher loading
rate causes a lower value for initiation and a higher value for propagation, although further
research is necessary to validate this last result.
In present work the influence of curing pressure of laminated composite on the interlaminar
fracture toughness under Mode II loading was investigated. Change in curing pressure will
create changes in the geometry, matrix content between layers, fibre volume fraction and
degree of wetting of fibre by matrix, which may eventually cause differences in fracture
toughness values. It is evident from the above literature review that both Mode I and Mode II
fracture toughness behavior of composites have been investigated. To the author’s
knowledge, there are very few published papers on the effect of curing pressure on Mode II
fracture toughness behavior. Therefore, it is important that the effect of curing pressure is
understood in relation to their effects on the fracture toughness behavior of GFRP so that
damage tolerance of these composites are understood. This study presents an investigating of
the effects of curing pressure on the Mode II interlaminar fracture toughness behavior of unidirectional GFRP laminates.
2. Materials and methods
2.1. Materials
The reinforcing phase used in the fabrication of laminated composites was unidirectional
glass fibre UD 200 with mass density 220 gsm while Araldite epoxy resin (LY556) and
hardener (HY951) mixed in the ratio 10:1 being the reinforced matrix phase. Fibre and Epoxy
were taken in 50:50 mass proportions. 10:1 Epoxy and hardener mixture was stirred well.
GFRP composite laminates of dimensions 250 × 250 mm with fibre stacking sequences in
zero degree direction were fabricated by compression moulding. A non-adhesive insert
(Teflon) of thickness within 13 microns was inserted in the neutral layer to serve as a precrack, as shown in Fig. 1. Three 12 layered laminates were cured at different pressures, 5 Psi,
400 Psi and 800 Psi, respectively, and one 16 layered laminate cured at 5Psi. All curing was
at room temperature for 24 hours. ENF specimens with dimensions 140×25 mm were cut
from each laminate using a water jet cutting process. Care was taken so that in each specimen
the Teflon insert (pre-crack) come at an edge, as shown in Fig. 1. This will act as an exterior
crack.
2.2. Mode II fracture toughness testing
Specimens were prepared as per ISO/CD 15114 standard [24]. ENF testing is carried out in a
Tinius Olsen H100KU Universal Testing Machine with a 100 kN load cell. Specimens were
subjected to three-point bending load in the transverse direction. Displacement control mode
of testing was preferred and crosshead speed of 1mm/min was maintained. Markings at the
side of the specimen helped to identify crack initiation and propagation. The loading is
analogous to a simply supported beam with concentrated load at the centre. Specimens are
subjected to combined bending and shear loads. The layers above the insert are subjected to
compression and the layers below are subjected to tension. Monotonically increasing load
was applied and the stress strain data was continuously obtained until failure. The mode II
fracture toughness value, GIIC , was obtained by using the following equation [25].
GIIC
9P  a 2

2 B(1 / 4 L3  3a 3 )
(1)
where, a is delamination crack length (mm), P is maximum load (N),  is displacement
(mm) B is width of specimen (mm).
Five replicate tests were conducted and the average fracture toughness was obtained.
Maximum shear force is induced at the neutral layer. Hence, top half of the specimen slides
over the bottom half at the neutral layer, which results in delamination as seen in Fig. 2. The
various stages of ENF loading are shown in Fig. 3.
3. Results and discussion
3.1. Breakdown of delamination process
Delamination in Mode II fracture is caused by the shear force between the separating
plies. There are two mechanisms involved in the processes of delamination. Cohesive fracture
that occurs within the matrix material between two plies, and the fibre/matrix interface
debonding that occurs at the interface of matrix and a single ply. The combination of these
two results in delamination. During fracture, energy stored in the laminate is released, and
this energy is termed as critical strain energy or fracture toughness.
Various process involved in ENF testing of GFRP Laminates are shown in Fig. 4.
During the initial stage of loading, the material is totally elastic and this can be proved by the
linearity of the stress-strain curve. At this stage, no or very little failure by matrix cracking
occurs. No other failures will be present at this stage. The laminate continues to take load
depending on the stiffness of the laminate. At some point, the curve become non-linear where
strain rate increases and the loading rate decreases. The laminate loses some of its stiffness
due to permanent failures. Since shear stress is maximum at the neutral layer, and also with
the presence of the Teflon insert, the first major failure is supposed to occur at the tip of the
pre-crack due to the stress concentration. Initiation of delamination can be visually observed
at a region somewhere between the non-linear initiation point and the peak stress. Once the
strain energy reached the critical strain energy of the material for Mode II crack propagation,
the crack starts to propagate suddenly, causing an abrupt drop in the load. After that, the load
begins to increase since the two separated half’s continue to take bending load until crushing
or tensile failure occurs at the top or bottom most extreme fibres ,which is not our concern
here.
3.2. Material and geometric stiffness
Stiffness of a laminate comes from two ways. First is the material stiffness which can be
measured from the slope of the stress-strain curve, as shown in Fig. 5. Young’s modulus
increases with the curing pressure as seen in Fig. 6(a). Also, it can be seen that the 12 and 16
layer laminates cured at the same pressure have same Young’s modulus values, since the only
difference between them is the thickness, the material composition remains same.
Geometric stiffness is due to effects of the width and thickness of the specimen, which is
known as the Section Modulus (I/Y). Since width of all the specimens is equal, thickness is
the only dimension that brings changes to the stiffness of the material. The slope of the loaddeflection curve gives the total stiffness of the laminate which includes both material and
geometric stiffness. Material and geometric stiffness offer different extent of contribution to
the total stiffness of the laminate, and thereby influence on the properties of laminates.
Comparison of Young’s modulus and bending stress at the time of delamination is shown in
Fig. 7. It can be clearly seen that the Young’s modulus of 12 and 16 Layer laminates cured at
5 Psi are equal, as discussed, but 16 Layer laminate failed earlier than the 12 Layer laminate,
even although they are supposed fail at the same stress. This premature failure is due to the
dominant shear stress in 16 Layer laminate due to the increased thickness. For the same
bending stress, thick laminates take more loads compared to thin laminates, and hence the
shear stress induced in thick laminates is higher than that of thin laminates load and thus fails
earlier.
3.3. Influence of thickness and Young’s Modulus on stiffness of laminate
Both Young’s modulus and thickness contribute to stiffness of the laminate. This can be seen
from Fig. 8. As shown in Fig. 8(a) the Young’s modulus is the same, but there is drastic
difference in stiffness due to the difference in thickness which can be seen in Fig. 8(b). In
Fig. 8(c), even although the laminate cured at 400 Psi is thicker than that cured at 800 Psi, the
total stiffness is lower. This is because the Young’s modulus of laminate cured at 800 Psi is
higher than that cured at 400 Psi, as seen in Fig. 8(d). From this, it is clear both Young’s
modulus and thickness contribute to total stiffness of the laminate.
Variation of stiffness with thickness for laminates with different Young’s modulus is shown
in Fig. 9(a). The variation is not linear but quadratic, as expected, because section modulus is
proportional to the square of thickness. Variation of stiffness with Young’s modulus for
laminates with different thickness is shown in Fig. 9(b). It varies linearly, as seen in Fig. 9(d).
Also, slope of the line of variation of thickness is higher than that of Young’s modulus. This
shows that the contribution of thickness to total stiffness is higher than that of Young’s
modulus. This can also be seen in Fig. 10.
As seen in Fig. 10, since there is a huge difference in thickness between 16 layer laminate
and 12 layer laminate cured at 800 Psi, it outweighs the contribution to stiffness of Young’s
modulus . Hence, 16 layer laminate has higher total stiffness than the rest of the laminates.
Stiffness difference among the laminates in turn influences some of the properties of the
laminates tested at similar conditions.
3.4. Influence of geometric stiffness on properties of laminates
As seen in Fig. 11(a), the Young’s modulus of the two laminates is the same so the difference
in stiffness among the laminates is due to geometric stiffness. The shear strength and bending
strength at the time of delamination of the laminate varies with stiffness but fracture
toughness remains unaffected, as seen in Fig. 11(c), since it is associated fracture of material
and the creation of new surface during crack propagation. In three-pointf tests, both bending
and shear loads co-exist. Failure can occur due to either of them depending on the material
and geometry of the structure. As mentioned previously, since there is a Teflon insert, the
failure occurs first at the tip of the pre-crack in the neutral layer because of delamination due
to shear. Due to this delamination failure, the top layer sliding over the bottom results in loss
of bending stiffness. Hence, there is a drop in bending stress. Thin laminates deflect more
than thicker ones for the same load. Hence, the strain induced in thin laminatesis higher and
so is the bending stress, as seen in Fig. 11(b). Thick laminates are stiffer and they will not
deflect much for same bending stress. They take more load compared to thin laminates for the
same bending stress and, hence the shear stress induced in thick laminates is higher than that
of thin laminates. This can be seen from Fig. 11(d). They behave like a short beam and the
shear stress becomes dominant. Hence, they fail far earlier, as seen in Fig. 5. Young’s
Modulus and Fracture toughness are independent of geometric dimensions of the laminate,
and hence they solely depend on the material. Material properties differ when the laminates
are cured at different pressures.
3.5. Influence of curing pressure on properties of laminates
Comparison was made between 12 layer laminates cured at different pressures whose
differences in thickness are minimal. The significant effect in properties is due to the material
and not due to geometry. As seen in Fig. 12(d), curing pressure influences the material
stiffness significantly. The microscopic cross sectional view of different laminates is shown
in Fig. 13.Increasing the curing pressure decreases matrix volume fraction and, in turn,
decreases the thickness of matrix layer between the layers, as seen in Fig. 14.
Increasing the curing pressure increases the Young’s modulus. This is because at high
pressure wetting of fibre with resin is more efficient, and properly wetted fibres are stiffer
than the resin itself. Also, due to high pressure curing, the fibre volume fraction will be high
,which results in high stiffness. As far as fracture toughness and shear stress are concerned,
too much matrix trapped between two adjacent layers is not good and, at the same time, too
thin a matrix layer is also not recommended. The thickness of the matrix layer between
adjacent layers plays an important role in the interlaminar shear strength and it should be of
optimum thickness. If the matrix layer is too thick the matrix breaks first and the crack
propagates in a direction perpendicular to fibre until it reaches any interface, and from there it
will propagate parallel to the fibre direction. If the matrix layer is too thin there won’t be
enough bonding between the plies. Also, resistance to crack propagation is only due to
adhesion between the matrix and fibre mat. Cohesive resistance won’t be there which results
in sudden crack propagation parallel to the fibre direction. Optimum thickness of matrix layer
offers both adhesive and cohesive resistance to the crack propagation. Increase the curing
pressure will reduce the thickness of matrix between the layers. Peak load at the time of
delamination first increases from 5 Psi to 400 Psi and then falls on further with increase in
pressure to 800 Psi.
This is due to the difference in thickness of matrix layer trapped between adjacent layers, as
seen in Fig. 15.
3.6. Toughness comparison of laminates
The fracture toughness comparison values of various laminates are presented in Table 1. As
can be seen from the results, different laminates have different fracture toughness values.
Toughness of a structure requires a balance between strength and ductility. To be tough, a
material should withstand both high stresses and strains. Brittle material might be stiffer but
may not be ductile enough to with stand higher strains, leading to sudden failure. If the
material is too ductile it will not be stiff enough to with stand higher stresses. Toughness can
be taken as the area under the stress-strain curve, and is shown for different laminates in Fig.
16. It can be seen that highly stiff 16 layer laminate collapse earlier due to dominant shear
stress, as explained previously. However, as seen in Fig. 16(d), 12 layer laminate cured at 800
Psi is stiff due to its material stiffness, and hence it take more stress but doesn’t with stand
the stress for long. 12 Layer laminate cured at 400 Psi is stiff as well as ductile so that it
takes high stress and high strain. It is the toughest laminate under investigation here and can
be highly recommended for crack resistance.
4. Conclusions
The effect of curing pressure on material stiffness, shear strength and the Mode II fracture
toughness has been investigated for different uni-directional GFRP laminates by using threepoint bend end notched flexure (ENF). In ENF testing, combined effect of bending and shear
could be seen. Shear force is the cause for delamination of composite materials under Mode
II fracture. It is shown that shear stress is influenced by the geometric stiffness as well as
material stiffness, but the fracture toughness remains unaffected since it is associated with
crack propagation and creation of new surfaces. The contribution of both geometric stiffness
as well as material stiffness to the total stiffness is investigated. The results obtained from this
study show that the fracture toughness is affected by change in curing pressure. The change
in fracture toughness is due to the difference in the thickness of matrix layer trapped between
adjacent layers. Amongst the specimens evaluated, the 400 Psi laminate exhibited highest
fracture toughness.
References
[1] ASTM D5528-01, Standard test method for Mode I interlaminar fracture toughness of
unidirectional fiber-reinforced polymer matrix composites, Annual Book of ASTM Standard
15.03 (2004).
[2] W.D. Bascom, Fractography of Composite Delamination, NASA Contractor Report
181965 (1990).
[3] F. Chen, S. Bazhenov, V. Hiltner, E. Baer, Flexural failure mechanisms in unidirectional
glass fibre reinforced thermoplastics, Composites Number (1) (1994).
[4] Jiang Zhou, Tianbai He, On the Analysis of the End-notched flexure specimen for
measuring Mode II fracture toughness of composite materials, Composites Science and
Technology 50 (1994) 209-213.
[5] D. Stevanovic, P.Y.B. Jar, S. Kalyanasundaram, A. Lowe, On crack-initiation conditions
for mode I and mode II delamination testing of composite materials, Composites Science and
Technology 60 (2000) 1879-1887.
[6] X. Li, L.A. Carlsson, P. Davies, Influence of fiber volume fraction on Mode III
interlaminar fracture toughness of gass/epoxy composites, Composites Science and
Technology 64 (2004) 1279–1286.
[7] Ramazan Kahraman, Mehmet Sunar, Bekir Yilbas, Influence of adhesive thickness and
filler content on the mechanical performance of aluminum single-lap joints bonded with
aluminum powder filled epoxy adhesive, Journal of Materials Processing Technology 205
(2008) 183–189.
[8] T. Ireman, J.C. Thesken, E. Greenhalgh, R. Sharp, M. Gadke, S. Maison, Y.F. Ousset, F.
Roudolff, A.L. Barbera, Damage propagation in composite structural elements-coupon
experiments and analyses, Composite Structures 36 (1996) 209-220.
[9] M. Patricio, R.M.M. Mattheij, Crack paths in composite materials, Engineering Fracture
Mechanics 77 (2010) 2251–2262.
[10] ZHANG SQ, JANG BZ, VALAIRE BT, SUHLING JC, A New criterion for composite
material mixed mode fracture analysis, Engineering fracture Mechanics 34 (3) (1989) 149169.
[11] Wenran Gong, Jinlong Chen, Eann A. Patterson, An experimental study of the behaviour
of delaminations in composite panels subjected to bending, Composite Structures 123 (2015)
9–18.
[12] Arun Krishnan, L. Roy Xu, An experimental study on the crack initiation from notches
connected to interfaces of bonded bi-materials, Engineering Fracture Mechanics 111 (2013)
65–76.
[13] Hansang Kim, Eugene Oh, H. Thomas Hahn, Kun-Hong Lee, Enhancement of fracture
toughness of hierarchical carbon fiber composites via improved adhesion between carbon
nanotubes and carbon fibers, Composites: Part A 71 (2015) 72–83.
[14] K.C. Jajam, H.V. Tippur, An experimental investigation of dynamic crack growth past a
stiff inclusion, Engineering Fracture Mechanics 78 (2011) 1289–1305.
[15] B. Ahmadi-Moghadam, F. Taheri, Fracture and toughening mechanisms of GNP-based
nanocomposites in modes I and II fracture, Engineering Fracture Mechanics 131 (2014) 329–
339.
[16] H. Saghafi, A. Zucchelli, R. Palazzetti, G. Minak, The effect of interleaved composite
nanofibrous mats on delamination behavior of polymeric composite materials, Composite
Structures 109 (2014) 41–47.
[17] Yuli Chen, Shengtao Wang, Bin Liu, Jianyu Zhang, Effects of geometrical and
mechanical properties of fiber and matrix on composite fracture toughness, Composite
Structures 122 (2015) 496–506.
[18] N. Baral, P. Davies, C. Baley, B. Bigourdan, Delamination behaviour of very high
modulus carbon/epoxy marine composites, Composites Science and Technology 68 (2008)
995–1007.
[19] F. Ducept, P. Davies, D. Gamby, Mixed mode failure criteria for a glass/epoxy
composite and an adhesively bonded composite/composite joint, International Journal of
Adhesion & Adhesives 20 (2000) 233-244.
[20] B. Cotterell, J.Y.H. Chia, K. Hbaieb, Fracture mechanisms and fracture toughness in
semicrystalline polymer nanocomposites, Engineering Fracture Mechanics 74 (2007) 1054–
1078.
[21] Yasuhide Shindo,Tomo Takeda, Fumio Narita, Nozomi Saito, Shinya Watanabe,
Kazuaki Sanada, Delamination growth mechanisms in woven glass fiber reinforced polymer
composites under Mode II fatigue loading at cryogenic temperatures, Composites Science
and Technology 69 (2009) 1904-1911.
[22] T. Lyashenko, N. Lerman, A. Wolf, H. Harel, G. Marom, Improved Mode II
delamination fracture toughness of composite materials by selective placement of proteinsurface treated CNT, Composites Science and Technology 85 (2013) 29–35.
[23] I. De Baere, S. Jacques, W.V. Degrieck, Study of the Mode I and Mode II interlaminar
fracture toughness behaviour of a carbon fabric reinforced thermoplastic, Polymer Testing 31
(2012) 322-332.
[24] ISO/CD 15114: Fibre-reinforced plastic composites: Determination of apparent mode II
interlaminar fracture toughness for unidirectionally reinforced materials.
[25] R.F. Gibson, Principles of Composite Material Mechanics, McGraw Hill, USA (1994)
395-397.
Figure captions
Fig. 1. A schematic of the ENF test specimen dimensions
Fig. 2. Sliding of top half over bottom half
Fig. 3. Various stages of delamination
Fig. 4. Process involved in Mode II delamination of GFRP laminates
Fig. 5. Material and geometric stiffness
Fig. 6. Young’s Modulus Calculation (a) 16 Layer-5Psi (b) 12 Layer-5Psi (c) 12 Layer-400Psi
(d) 12 Layer-800Psi
Fig. 7. Comparison of (a) Young’s Modulus (b) Bending stress at the time of delamination
Fig. 8. Effect of thickness and Young’s Modulus on stiffness
Fig. 9. Variation of stiffness due to thickness and Young’s Modulus
Fig. 10. Stiffness comparison of laminates
Fig. 11. Effect of geometric stiffness on (a) Young’s Modulus (b) Bending stress (c) Fracture
toughness (d) Shear stress
Fig. 12. Effect of curing pressure on (a) Bending stress (b) Shear stress (c) Fracture toughness (d)
Young’s Modulus
Fig. 13. Microscopic cross sectional view of laminate cured at (a) 5Psi (b) 400Psi (c) 800Psi
Fig. 14. Effect of curing pressure on (a) Matrix volume fraction (b) Thickness of matrix layer
Fig. 15. Effect of thickness of matrix layer on shear strength and Fracture toughness
Fig. 16. Toughness calculation (a) 16 Layer-5Psi (b) 12 Layer-5Psi (c) 12 Layer-400Psi
(d) 12 Layer-800Psi
Fig. 1. A schematic of the ENF test specimen dimensions
Fig. 2. Sliding of top half over bottom half
Fig. 3. Various stages of delamination
Fig. 4. Process involved in Mode II delamination of GFRP laminates
Fig. 5. Material and geometric stiffness
Fig. 6. Young’s Modulus Calculation (a) 16 Layer-5Psi (b) 12 Layer-5Psi (c) 12 Layer-400Psi
(d) 12 Layer-800Psi
Fig. 7. Comparison of (a) Young’s Modulus (b) Bending stress at the time of delamination
Fig. 8. Effect of thickness and Young’s Modulus on stiffness
Fig. 9. Variation of stiffness due to thickness and Young’s Modulus
Fig. 10. Stiffness comparison of laminates
Fig. 11. Effect of geometric stiffness on (a) Young’s Modulus (b) Bending stress (c) Fracture
toughness (d) Shear stress
Fig. 12. Effect of curing pressure on (a) Bending stress (b) Shear stress (c) Fracture toughness (d)
Young’s Modulus
Fig. 13. Microscopic cross sectional view of laminate cured at (a) 5Psi (b) 400Psi (c) 800Psi
Fig. 14. Effect of curing pressure on (a) Matrix volume fraction (b) Thickness of matrix layer
Fig. 15. Effect of thickness of matrix layer on shear strength and Fracture toughness
Fig. 16. Toughness calculation (a) 16 Layer-5Psi (b) 12 Layer-5Psi (c) 12 Layer-400Psi
(d) 12 Layer-800Psi
Table captions
Table 1: Comparison of fracture toughness for various laminates
Table 1: Comparison of fracture toughness for various laminates
Laminate types
Fracture toughness GIIC (N/m) 
16Lyr5psi
1634  56
12Lyr5psi
1659  52
12Lyr400psi
2642  46
12Lyr800psi
1643  58