* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Matt Wolf - CB East Wolf
Survey
Document related concepts
Transcript
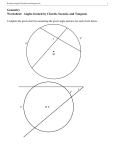
Mr. Wolf Monday 12/15/08 Geometry Grades 10-12 Unit 8: Circles Arcs and Central Angles Materials and Resources: Warm-up (1 per student) Arcs and Central Angles sheet (1 per student) protractors, rulers (1 pair per student) Exit Ticket (1 per student) PA Standards Addressed: Instructional Objectives: Students will be able to define and identify minor arcs, major acrs, central angles, adjacent arcs, and congruent arcs. Students will be able to find the measure of central angles and arcs using protractors. Students will be able to calculate the measure of central angles and arcs by applying the Arc Addition Postulate. Time 10 min 1 min min Activity Warm-up Agenda Arcs and Central Angles Pg. 341 Classroom Exercises #1-13 1 min 5 min Agenda Conclusion Description Pass out the Warm-up and review solutions. Review the goals for the day. Modeling: Guiding: Independent Practice: Assessment: Modifications: Students with special needs… Advanced students… Revisit goals and identify whether they were met. Pass out the Exit Ticket and collect at the bell. Homework: Pg. 341 Written Exercises #1-6, 10, 11 Lesson Reflection: Geometry Fall 2008 Name: ________________________ Warm-up Given CB and CD are tangent to circle A and m BCD 24 . a. What is true about CB and CD ? Why is this true? b. Find measures of DBC and BDC . c. What is true about AB and AD ? Why is this true? d. Find measures of ABC and ADC . e. Find measures of ABD and ADB . Geometry Fall 2008 Name: ________________________ Warm-up Given CB and CD are tangent to circle A and m BCD 24 . a. What is true about CB and CD ? Why is this true? b. Find measures of DBC and BDC . c. What is true about AB and AD ? Why is this true? d. Find measures of ABC and ADC . e. Find measures of ABD and ADB . Geometry Fall 2008 Name: ________________________ Arcs and Central Angles Definitions: A central angle is an angle with its vertex at the center of a circle. An arc is a segment on the perimeter of a circle with endpoints on a circle. The measure of an arc is defined to be the measure of its central angle. A minor arc is formed by two points on a circle with measure less than 180°. A semicircle is formed by two points on a circle with measure equal to 180°. A major arc is formed by two points on a circle with measure greater than 180°. *Major arcs are named with three points whereas minor arcs are named with only two. Activity 1: Circle A: 1) Draw radii AB and AC . Conclusion Questions: 1) Using your protractor, measure the smaller part of BAC . mBAC ______ 2) Minor arc BC has measure of ______. 3) Circles have a total of ______°. 4) Calculate the measure of the larger part of BAC . 5) Major arc BDC has measure of ______. mBAC ______ Definition: Adjacent arcs of a circle are arcs that have exactly one point in common. Activity 2: Circle R: 1) Draw radii RS , RT , and RU . Conclusion Questions: 1) Using your protractor, measure the smaller part of SRT . mSRT ______ 2) Minor arc ST has measure of ______. 3) Using your protractor, measure the smaller part of TRU . mTRU ______ 4) Minor arc TU has measure of ______. 5) Without using your protractor, find the measure of SRU . mSRU ______ 6) What postulate allows us to find the measure of SRU without using a protractor? 7) Minor arc SU has measure of ______. 8) Major arc SWU has measure of ______. 9) What kind of arcs are ST and TU? What point do they share in common? 10) Complete the theorem: The measure of the arc formed by two adjacent arcs is equal to _____________________ ________________________________________________________________________ Definition: Congruent arcs are arcs, in the same circle or in congruent circles, that have equal measures. Activity 3: Circle M: 1) Draw radii MP and MQ . 2) Using your protractor, find the measure of PMQ. mPMQ ______ 3) Use your protractor to create another arc in the circle with the same measure as PMQ. To do this, place your protractor on MP and mark a point on the circle at the same measure as PMQ. 4) Label this point N. Conclusion Questions: 1) Using your protractor, measure the smaller part of PMQ . mPMQ ______ 2) Minor arc PQ has measure of ______. 3) Using your protractor, measure the smaller part of NMP . mNMP ______ 4) Minor arc NP has measure of ______. 5) Without using your protractor, find the measure of NMQ . mNMQ ______ 6) Minor arc NQ has measure of ______. 7) Major arc NQ has measure of ______. 8) Complete the theorem: In the same circle or in congruent circles, two minor arcs are congruent if and only if ________________________________________________________________________ Definitions: A central angle is an angle with its vertex at the center of a circle. An arc is a segment on the perimeter of a circle with endpoints on a circle. The measure of an arc is defined to be the measure of its central angle. A minor arc is formed by two points on a circle with measure less than 180°. A semicircle is formed by two points on a circle with measure equal to 180°. A major arc is formed by two points on a circle with measure greater than 180°. *Major arcs are named with three points whereas minor arcs are named with only two. Adjacent arcs of a circle are arcs that have exactly one point in common. Congruent arcs are arcs, in the same circle or in congruent circles, that have equal measures. Arc Addition Postulate – The measure of the arc formed by two adjacent arcs is the sum of the measures of these two arcs. Arc Congruency Theorem – In the same circle or in congruent circles, two minor arcs are congruent if and only if their central angles are congruent. Directions: Match the letter of the definition with the term it defines. central angle _____ arc _____ measure of an arc _____ minor arc _____ semicircle _____ major arc _____ adjacent arcs _____ congruent arcs _____ Arc Addition Postulate _____ Arc Congruency Theorem _____ A. arcs that have exactly one point in common B. formed by two points on a circle with measure equal to 180° C. In the same circle or in congruent circles, two minor arcs are congruent if and only if their central angles are congruent. D. an angle with its vertex at the center of a circle E. equal to the measure of its central angle F. arcs in the same circle or in congruent circles that have equal measures G. The measure of the arc formed by two adjacent arcs is the sum of the measures of these two arcs. H. a segment on the perimeter of a circle with endpoints on a circle I. formed by two points on a circle with measure greater than 180° J. formed by two points on a circle with measure less than 180° Directions: Match the letter of the definition with the term it defines. central angle _____ arc _____ measure of an arc _____ minor arc _____ semicircle _____ major arc _____ adjacent arcs _____ congruent arcs _____ Arc Addition Postulate _____ Arc Congruency Theorem _____ A. arcs that have exactly one point in common B. formed by two points on a circle with measure equal to 180° C. In the same circle or in congruent circles, two minor arcs are congruent if and only if their central angles are congruent. D. an angle with its vertex at the center of a circle E. equal to the measure of its central angle F. arcs in the same circle or in congruent circles that have equal measures G. The measure of the arc formed by two adjacent arcs is the sum of the measures of these two arcs. H. a segment on the perimeter of a circle with endpoints on a circle I. formed by two points on a circle with measure greater than 180° J. formed by two points on a circle with measure less than 180°