Download supplemental sheet #7

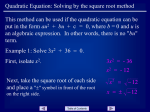
SUPPLEMENTAL SHEET #7
TOPIC: SOLVING QUADRATIC EQUATIONS
Any equation of type ax2 + bx + c = 0 where a, b, and c are constants and a <> 0, is in
standard form for a quadratic equation.
Solution by factoring:
Quadratic equations can be factored to solve for x. Examples:
1. Solve 3x2 + x - 2 = 0 for x.
Solution: Factor.
(3x - 2)(x + 1) = 0
Use the principle of zero products,
which says, if ab = 0, either
a, b, or both must be
equal to zero.
3x - 2 = 0, x + 1 = 0
3x = 2 , x = -1
x = (2/3)
x = -1, (2/3)
2. Solve 3x2 + 5x = 0 for x.
Solution: Factor.
x(3x + 5) = 0
Use the principle of zero products.
x = 0, 3x + 5 = 0
3x = -5
x = -(5/3)
x = 0, -(5/3)
Quadratic equations of type ax2 + c = 0 can be solved by solving for x. Example:
3. Solve 3x2 = 6 for x.
Solution: Recognize that the equation is quadratic because it is the
same as 3x2 - 6 = 0.
Divide each side by 3.
x2 = 2
Take the square root of each side.
x = SQRT(2), -(SQRT(2))
Taken from:
http://library.thinkquest.org/20991/alg2/quad.html
Solution by completing the square:
Some quadratics are fairly simple to solve because they are of the form "something-withx squared equals some number", and then you take the square root of both sides. An
example would be:
(x – 4)2 = 5
x – 4 = ± sqrt(5)
x = 4 ± sqrt(5)
x = 4 – sqrt(5) and x = 4 + sqrt(5)
Unfortunately, most quadratics don't come neatly squared like this. For your average
everyday quadratic, you have to use the technique of completing the square to rearrange
the quadratic into the neat format demonstrated above. For example:

Find the x-intercepts of y = 4x2 – 2x – 5.
First off, remember that finding the x-intercepts means setting y equal to zero and
solving for the x-values, so this question is really asking you to "Solve 4x2 – 2x –
5 = 0".
This is the original problem.
Move the loose number over to the
other side.
4x2 – 2x – 5 = 0
4x2 – 2x = 5
Divide through by whatever is
multiplied on the squared term.
Take half of the coefficient (don't
forget the sign!) of the x-term, and
square it. Add this square to both sides
of the equation.
Convert the left-hand side to squared
form, and simplify the right-hand side.
(This is where you use that sign that
you kept track of earlier.)
Square-root both sides, remembering
the "±" on the right-hand side.
Simplify as necessary.
Solve for "x =".
Remember that the "±" means that you
have two values for x.
The answer can also be written in rounded form as
You will need rounded form for "real life" answers to word problems, and for graphing.
But in most other cases, you should assume that the answer should be in "exact" form,
complete with all the square roots.
When you complete the square, make sure that you are careful with the sign on the xterm when you multiply by one-half. If you lose that sign, you can get the wrong answer
in the end. Also, don't be sloppy and wait to do the plus/minus sign until the end. On your
tests, you won't have the answers in the back, and you will likely forget to put the
plus/minus into the answer. Besides, there's no reason to go ticking off your instructor by
doing something wrong when it's so simple to do it right. On the same note, make sure
you draw in the square root sign, as necessary, when you square root both sides. Don't
wait until the answer in the back of the book "reminds" you that you "meant" to put the
square root symbol in there. If you get in the habit of being sloppy, you'll only hurt
yourself!

Solve x2 + 6x – 7 = 0 by completing the square.
Do the same procedure as above, in exactly the same order. (Study tip: Always
working these problems in exactly the same way will help you remember the
steps when you're taking your tests.) Copyright © Elizabeth Stapel 2000-2007 All
Rights Reserved
This is the original problem.
x2 + 6x – 7 = 0
Move the loose number over to the other side.
x2 + 6x
=7
Take half of the x-term (that is, divide it by
two) (and don't forget the sign!), and square it.
Add this square to both sides of the equation.

Convert the left-hand side to squared form.
Simplify the right-hand side.
(x + 3)2 = 16
Square-root both sides. Remember to do "±"
on the right-hand side.
x+3=±4
Solve for "x =". Remember that the "±" gives
you two solutions. Simplify as necessary.
x=–3±4
= – 3 – 4, –3 + 4
= –7, +1
Solve x2 + 6x + 10 = 0.
Apply the same procedure as before: Copyright © Elizabeth Stapel 2000-2007 All
Rights Reserved
This is the original equation.
Move the loose number over to the other side.
x2 + 6x + 10 = 0
x2 + 6x = – 10
Take half of the coefficient on the x-term (that
is, divide it by two) (don't forget the sign!),
and square it. Add this square to both sides of
the equation.
Convert the left-hand side to squared form.
Simplify the right-hand side.
Note: If you don't know about complex
numbers yet, then you have to stop at this
step, because a square can't equal a negative
number! Otherwise, proceed...
Square-root both sides. Remember to put the
"±" on the right-hand side.
(x + 3)2 = –1
Note the square root of a negative number!
Solve for "x =", and simplify as necessary.
x = –3 ± i
If you don't yet know about complex numbers (the numbers with "i" in them), then you
would say that this quadratic has "no solution". If you do know about complexes, then
you would say that this quadratic has "no real solution" or that is has a "complex
solution". In either case, this quadratic had no "real" solution. Since solving "(quadratic)
= 0" for x is the same as finding the x-intercepts (assuming the solutions are real
numbers), it stands to reason that this quadratic should not intersect the x-axis (since xintercepts are "real" numbers), and you can see below that it doesn't:
Taken from:
www.purplemath.com
Solution by use of the quadratic formula:
You can solve ANY quadratic equation by using the quadratic formula.
This comes in handy when a quadratic equation does not factor or is
difficult to factor.
Step 1: Simplify each side if needed.
This would involve things like removing ( ), removing fractions,
adding like terms, etc.
To remove fractions: Since fractions are another way to write
division, and the inverse of divide is to multiply, you remove
fractions by multiplying both sides by the LCD of all of your
fractions.
Step 2: Write in standard form,
, if needed.
If it is not in standard form, move any term(s) to the appropriate
side by using the addition/subtraction property of equality.
Also, make sure that the squared term is written first left to
right, the x term is second and the constant is third and it is set
equal to 0.
Step 3: Identify a, b, and c.
When the quadratic equation is in standard
form,
, then a is the coefficient in front of
the term, b is the coefficient in front of the x term, and c is
the constant term.
Step 4: Plug the values found in step 3 into the quadratic formula.
When
, then
Step 5: Simplify if possible.
Solve
by using the quadratic formula.
Step 1: Simplify each side if needed.
This quadratic equation is already simplified.
Step 2: Write in standard form,
, if needed.
This quadratic equation is already in standard form.
Step 3: Identify a, b, and c.
a, the number in front of x squared, is 2.
b, the number in front of x, is -5.
c, the constant, is 1.
Make sure that you keep the sign that is in front of each of these
numbers.
Next we will plug it into the quadratic formula. Note that we are only
plugging in numbers, we don't also plug in the variable.
Step 4: Plug the values found in step 3 into the quadratic formula
AND
Step 5: Simplify if possible.
*Quadratic formula
*Plug in values found above for a, b,
and c
*Simplify
Solve
by using the quadratic formula.
Step 1: Simplify each side if needed.
This quadratic equation is already simplified.
Step 2: Write in standard form,
, if needed.
This quadratic equation is already in standard form.
Step 3: Identify a, b, and c.
a, the number in front of x squared, is 1.
b, the number in front of x, is 0.
Note that b is 0 because the x term is missing.
c, the constant, is 9.
Make sure that you keep the sign that is in front of each of these
numbers.
Next we will plug it into the quadratic formula. Note that we are only
plugging in numbers, we don't also plug in the variable.
Step 4: Plug the values found in step 3 into the quadratic formula
AND
Step 5: Simplify if possible.
*Quadratic formula
*Plug in values found above for a, b,
and c
*Simplify
*Square root of a negative 1 is i
Solve
by using the quadratic formula.
Step 1: Simplify each side if needed.
This quadratic equation is already simplified.
Step 2: Write in standard form,
, if needed.
*Inverse of add. 6x is sub. 6x
*Quad. eq. in standard form
Step 3: Identify a, b, and c.
a, the number in front of x squared, is 1.
b, the number in front of x, is -6.
c, the constant, is 9.
Make sure that you keep the sign that is in front of each of these
numbers.
Next we will plug it into the quadratic formula. Note that we are only
plugging in numbers, we don't also plug in the variable.
Step 4: Plug the values found in step 3 into the quadratic formula
AND
Step 5: Simplify if possible.
*Quadratic formula
*Plug in values found above for a, b,
and c
*Simplify
Taken from
http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut1
7_quad.htm