Download Lecture_11p2_Optimization_68

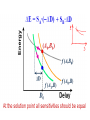
Logic Optimization
Mohammad Sharifkhani
Reading
• Textbook II, Chapters 5 and 6 (parts
related to power and speed.)
• Following Papers:
– Nose, Sakurai, 2000
– Broderson et. al. 2002 (True Power Min.)
– Zyuban, 2002
Optimization
• Only speed has been covered
– In most cases, power plays a significant role
– Power and delay optimization
– Delay constraint, power opt. or reverse
Portability
Energy density
Power sources
Energy model
Dynamic Power Dissipation
Vdd
Vin
Vout
CL
2
dd
L
Energy/transition = C * V
L
Power = Energy/transition * f = C * V
2
dd
*f
Not a function of Ltransistor
sizes!
dd
Need to reduce C , V , and f to reduce power.
Modification for Circuits with Reduced Swing
Vdd
Vdd
Vdd -Vt
CL
E0
1
= CL  Vdd   Vdd – Vt 
Can exploit reduced sw ing to low er power
(e.g., reduced bit-line swing in memory)
Node Transition Activity and Power
Consider switching a CMOS gate for N clock cycles
E N = CL  V dd2  n N 
EN : the energy consumed for N clock cycles
n(N ): the number of 0->1 transition in N clock cycles
EN
2
n N 
P avg = lim --------  fclk =  lim ----------- C  Vdd  f clk
N   N 
N N
L
0  1 =
n N 
lim -----------N N
P avg = 0 1  C  Vdd 2  f clk

L
Alpha-power based delay model
Optimization Goals
When both power and delay are important, how
can we optimize?
– How about minimization of Energy x Delay?
– What if one is more important?
– What are the variables in design optimization?
• Usually the designs are either power or delay
(speed) limited
• Can we optimize for the highest speed and
reduce the VDD until we get to the desired
speed?
Performance Optimization
Problem: Power minimization for a
given speed
•
•
•
•
•
•
Lower power  Lower VDD
Lower VDD  A slower design
A slower design  Lower Vth
Lower Vth  Higher leakage
Higher leakage  Higher power
Goal:
– Optimum VDD, Vth (for a given delta Vth)
Problem: Power minimization for a
given speed
• Optimal Vth, VDD (given process
parameters including variations)
• Step 1: calculation of delay, energy vs.
design variables
Ld is logic depth.
Problem: Power minimization for a
given speed
• Given td and Ld, Vthmax can be obtained based on VDD
• Given ΔVth, Vthmin can be calculated
The formula of power dissipation can be
derived, which is denoted as P(VDD).
When the clock frequency is given, we
differentiate P(VDD) with respect to VDD
and set the resultant expression to zero 
too difficult to solve, except with a lot of
appx.
Power Minimization Results
• Using Taylor expansion.
Assuming typical values for the parameters such that Ns=0.048
(S-factor=80mV/decade and TmaX=400K) and alpha=1.3,
PLEAK,max is calculated to be about 30% of the total power
Power Minimization Results
• Calculated under
various
– a (activity factor)
– f (clock freq)
• Numarical solution
of the original eq. is
also possible
• Approximations
made to achieve
the closed form
solution is
acceptable
Reults
• Again, equations
matches well with
the numerical
results
Results
• When logic depth
changes, the
optimal values for
VDD and Vth
changes as well.
Cost function based opt.
• What if we have multiple design tuning
variables?
– Vdd, size, threshold voltage, architecture, etc…
– Each tuning variable relates Energy to Delay in a
certain pattern
• A simplistic approach:
– Design for the highest speed, then reduce Vdd to
achieve a constraint (e.g., delay)
– Wrong!
• Goal:
– What is the proper setting for the design variable
under optimum situation?
Cost function based opt.
• Other cost functions can also be used:
• Where E0 and D0 are lower bounds for a
give design
• η is the Hardware Intensity
• Optimum is when the cost function is
minimized
• Hence:
Cost function based opt.
• A logic can be designed in a fixed supply
voltage with different design variable (size)
– Different designs
• Each design corresponds to a different
hardware intensity η
– We can re-interpret the design variable (size)
as a different η
Cost func. Based opt.
The solid line is the ED
curve when a tuning
variable (e.g, size)
changes under fixed
Vdd.
Dashed lines:
Each set of dashed
line corresponds to a
fixed Fc=A for that
particular η based on:
Actual hardware
delay, energy
relation wrt e.g.
size(η)
Contours based on Fc
function and η.
Independent of
hardware
For a given η,the smallest value of Fc can be found at the intersection between
the lowest dashed line (related to that η) and the solid line (related to the
actual hardware).
Hence, η corresponds to a particular value of the tuning variable (e.g. size).
Cost func. Based opt.
The solid line is the ED
curve when a tuning
variable (e.g, size)
changes under fixed
Vdd. .
Dashed lines:
Each set of dashed
line corresponds to a
fixed Fc=A for that
particular η based on:
Actual hardware
delay, energy
relation wrt e.g.
size(η)
Contours based on Fc
function and η.
Independent of
hardware
For a given η,the smallest value of Fc can be found at the intersection between
the lowest dashed line (related to that η) and the solid line (related to the
actual hardware).
When you are tuning the size  as if you are changing the η.
Cost func. Based opt.
• The following relationship holds at this point:
• Given the fact that
– We have
% value of power
% value of performance
Hardware intensity (η) is the ratio of the relative increase in the energy
to the relative gain in performance locally achievable through tuning a
design variable (e.g., size or logic restructuring) at a give supply
voltage.
Cost func. Based opt.
• Relationship with
supply voltage
• One can use
simulation to find Ev
and Dv for a given
design under various
η
Cost func. Based opt.
• Let’s solve minimal E(v, η) for a limited
D(v, η), hence:
• Hence we have:
What it means?
In an optimal design, the
Cost func. Based opt.
• Hence, for a given supply voltage v, an optimal η
can be achieved such that the relative gain in
speed/ relative increase in power for variation of
v (Dv/Ev) is equal to the relative gain in speed/
relative increase in power for variation of( η.)
• Simple words: At the optimal point, the relative
sensitivities of E and D to all design variables
must be the same
The energy-efficient design is achieved when
the marginal costs of all the tuning variables
are balanced
Cost func. Based opt.
• Example: if for a given supply voltage Dv=1 and
Ev=2  Other tuning variable (e.g., sizing) must
be such that η = 2  1% increase in delay and
2% saving in energy
• The notion that design for the highest speed and
reduce the supply voltage does not provide
optimum result
• Ex: if Dv=1, Ev=2 and sizing is optimal for η = 4
(circuit is not optimal)
Performance Optimization
• In most applications the case is not clear
as which cost function has to be minimized
• There is usually a bound (constrain) on a
certain design parameter:
– Delay
• Goal:
– What is the methodology of optimization for
delay/power constrained design?
Performance Optimization
Performance Optimization
Tuning variables
Step by step optimization
Step1
• Find the sensitivity of Energy to various design
variables
• Find the sensitivity of Delay to various design
variables
Step2
• The true power minimization method always
exploits the tuning variable with the largest
capability for energy reduction. This ultimately
leads to the point where the energy reduction
potentials of all tuning variables are equalized.
Load width
Input width
Delay time
increases the
leakage E over
one clock cycle
In single variable optimization
we go along with the variable
with the highest potential for
energy reduction
-From logical effort we know that the delay is
minimized when all stage efforts are the same (heff=4)
-Large last stages
-Let’s resize the last stages to save power  delay
increase (dinc)
Trans. Sizing
The energy increase due to the VDD raise is compensated by tuning W
Consistent with the
observations made in
the first approach