Download California Algebra 1 Unit 8

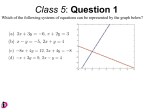
Algebra 1 Unit 4
1.
Students will be able to solve graphically a system of two linear equations in two
variables. (Section 6.1)
Page 279
1 – 8, 15 – 23
2.
Students will be able to solve a system of two linear equations in two variables
using the substitution method. (Section 6.2)
Page 284
5 – 15 odd, 29, 30, 31, 33, 36
*
Quiz 1
3.
Students will be able to solve a system of equations using the addition/elimination
method. (Section 6.3)
Page 290
1 – 7 odd, 10 – 14 even, 17 – 22
4.
Students will be able to solving a system of equations and recognize when there
is no solution or when there are an infinite number of solutions. (Section 6.2)
Worksheet 4
1 - 13
5.
Students will be able to solve word problems using a system of equations.
(Section 6.4)
Worksheet 5
1 – 10
*
Quiz 2
6.
Students will be able to solve coin problems using a system of equations.
Worksheet 6
1-8
7.
Students will be able to graph linear inequalities on a coordinate grid.
(Section 6.5)
Page 305
1 – 20
8.
Students will be able to graph a system of linear inequalities. (Section 6.6)
Page 312
1–9
*
Quiz 3
Review
Page 319
Worksheet
Algebra 1 Unit 4
6 – 8, 10 – 14, 19 – 21, 25 – 27, 29 – 33, 36 - 39
1 - 12
-1-
Worksheet 4
Use the graph at the right to determine whether the lines have
y
one solution, no solution, infinite solutions.
1.
line 4 and line 2
line 3
line 4
2.
line 1 and line 2
3.
line 3 and line 4
4.
line 1 and line 3
line 1
x
line 2
5.
Which multiple choice ordered pair could be a solution of the system graphed?
A.
(2,2)
B.
(– 2, 2)
y
C.
(– 2, – 2)
D.
(2, – 2)
x
6.
Which multiple choice ordered pair could be a solution of the system graphed?
y
x
7.
A.
(2, 0)
B.
(0, 2)
C.
(– 2, 0)
D.
(0, – 2)
Which multiple choice shows the solution to this system
A. (3, – 4)
Algebra 1 Unit 4
B. (1, 6)
C. no solution
-2-
y = – 2x + 2
2x + y = 8
D. infinitely many solutions
8.
At what point do the lines represented by x + y – 4 = 0
–2x + y – 1 = 0 intersect?
and
Solve each system of equations by graphing. If the two lines intersect, name the point
where they cross. If the two equations produce parallel lines, write no solution. If the
two equations produce the same line, write infinite number of solutions.
9.
y= x+1
10.
y=x–2
11.
y=x+4
y= x+2
y=–x+6
y–x=4
Solve each system of equations algebraically.
Remember, if the variables disappear and you get a true result that means there are an
infinite number of solutions.
A false result means that the equations have no solution.
12.
2x + 4y = 5
4x + 8y = – 9
Algebra 1 Unit 4
13.
-3-
3x – y = 4
–9x + 3y = – 12
Worksheet 5
Translate to a system of equations with two variables and solve.
1.
Two sodas and two servings of pie cost $1.80. Three sodas and one serving
of pie cost $2.00. Find the cost of each.
2.
The sum of two numbers is 12. Their difference is 4. Find the two numbers.
3.
Altogether the number of girls and boys in an algebra class totals 27.
The number of girls is 3 more than twice the number of boys. How many boys are
there? How many girls are there?
4.
Two eggs and two slices of bacon have a total of 22 grams of protein.
Two eggs and four slices of bacon have a total of 32 grams of protein.
Find the number of grams of protein in each food.
5.
 X and  Y are complementary. (They total 90°). The measure of  X is
50° more than  Y. Find the measure of each angle.
Algebra 1 Unit 4
-4-
6.
The sum of two numbers is 85. Their difference is 11. Find the two numbers.
7.
The sum of two numbers is 27. One number is 5 more than the other. Find
the two numbers.
8.
Three magazines and one candy bar costs $4.50 Two magazines and two candy
bars cost $4.00. Find the cost of one magazine. Find the cost of one candy bar.
9.
Two angles are supplementary. (They total 180°). One angle measures 3 times
the other angle. Find the measure of both angles.
10.
6 apples and 4 lemons weigh 70 ounces. 10 apples and 6 lemons weigh 114 ounces.
a. Find the weight of one apple.
b. Find the weight of one lemon.
c. Find the weight of one apple and one lemon together.
Algebra 1 Unit 4
-5-
Worksheet 6
1.
Beth has 12 coins in her purse. The coins are all nickels and dimes. The
total value of the coins is 95¢. How many of each does she have?
2.
Earl has 20 coins, all dimes and quarters. How many of each does he have, if their
total value is $3.80?
3.
Sheila has 26 coins in her toy bank. They are all nickels and dimes, and their total
value is $2.45. How many dimes does she have?
4.
John has 15 bills in his wallet. They are all $1 bills and $5 bills. If the total value
of these bills is $43, how many of each does he have?
Algebra 1 Unit 4
-6-
5.
Ms Swenson puts quarters and nickels aside for the parking meter. She has a
total of 18 coins, and they are worth $3.10. How many quarters does she have?
6.
21 tickets were sold to the ballet. Children tickets cost $5 each and adult
tickets cost $7 each. If a total of $129 was made, how many children tickets
were sold?
7.
See’s Candy sold 35 boxes of chocolates. Some boxes were small boxes and
some were large boxes. If the small boxes weighed 1 pound and the large boxes
weighed 2 pounds and a total of 50 pounds were sold, how many large boxes were
sold?
8.
Determine whether (2,0) is a solution of the system of equations.
2x = 4 – y
5x + 3y = 10
Algebra 1 Unit 4
-7-
Review
In problems 1 – 3 a system of equations has been graphed. State how many solutions
each system has. Answer with one of the following multiple choice responses.
A. one solution B. two solutions C. no solution
1.
2.
D. an infinite number of solutions
3.
4.
Solve this system:
3x = 5y
x + 2y = – 11
5.
Solve this system by substitution:
x = 5y – 8
3y + 2x = – 3
6.
The sum of two numbers is 98. Their difference is 48. Find the two numbers
by writing two equations using two variables and solving.
Algebra 1 Unit 4
-8-
7.
Two adults and 5 students paid $77 for their tickets for the Mammoth Cave tour.
Two adults and 7 students paid $95 for their tickets. Find the adult price and
the student price of the tour. (Write two equations using two variables and
solve.)
8.
 A and  B are complementary. (They total 90°). The measure of  B is
40° more than  A. Find the measure of each angle.
Answer true or false for each statement in problems 9 - 11
9.
The system
x+y = 1
x+y = 2
has no solution.
10.
When two lines are parallel they have no solution.
11.
(4, – 3) is a solution of the system
12.
Find the value of ‘ x ‘ in this system:
x + 4y = – 8
x= y+4
x + 6y = 25
Select the correct multiple choice response.
A. 3
Algebra 1 Unit 4
B. – 3
C. 7
-9-
D. – 7
E. 0