* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download e/ Natural Log
Survey
Document related concepts
Exact solutions in general relativity wikipedia , lookup
Schrödinger equation wikipedia , lookup
Differential equation wikipedia , lookup
Partial differential equation wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Schwarzschild geodesics wikipedia , lookup
Transcript
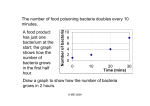
e/ Natural Log Starting with the graph y = ex, write and equation of the graph that results from 1. shifting 2 units down 2. shifting 2 units right 3. reflecting about the x-axis 4. reflecting about the y-axis Find the inverse function of 5. y = ln(x + 3) 6. y = 2(x + 3) Express as a single logarithm 7. 2 ln 4 - ln 2 8. ln x + a ln y - b ln z Evaluate each logarithm to six decimal places 9. log25 10. log526.05 Solve each equation for x 11. ex = 16 12. ln x = -1 13. ln(2x – 1) = 3 14. e(3x – 4) = 2 15. 2(x-5) = 3 16. ln x + ln(x -1) = 1 17. ln(ln x) = 1 18. If a bacteria population starts with 100 bacteria and doubles every three hours, then the number of bacteria after t hours is n = f(t) = 100 ∙ 2t/3 a) find the inverse function b) how many hours will it take for the population to reach 50,000?