Download ALGEBRA I Lesson 9-3

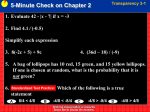
ALGEBRA I
LESSON 9-3
Pg. 489-493
FACTORING TRINOMIALS (x2 + bx + c)
(Issue 10-by-10 Factorization Sheets as study aids)
Review:
Trinomial: A polynomial with three parts (the sum of three monomials)
“FOIL”: First, Outside, Inside, and Last (to multiply two binomials)
Now:
We will learn to factor, then solve trinomials with a leading coefficient of “1” attached to x 2 term
TERM:
Factor Pair: Two numbers multiplied together to equal a third number (Ex. (6)(7) = 42), so 6
and 7 are a factor pair of 42.
FOIL (x + 2) (x+3)
Factor 1
Factor 2
F
O
I
L
= (x)(x) +(x)(3)+(2)(x) + (2)(3)
= x2 + 3x + 2x + 6
= x2 + 5x + 6 (This is the resulting TRINOMIAL)
or in general terms for all cases:
= x2 + bx + c where b = 5 and c = 6
When factoring a TRINOMIAL, the key concept to remember is this:
- The “c” is always equal to the product of the two numbers (factor pair)
(2)(3) = 6 (the “c” term of the original trinomial)
- The “b” is always equal to the sum of the same factor pair
2 + 3 = 5 (the “b” term of the original trinomial)
Steps for Factoring Trinomials:
1. Identify all the factors of “c” and list them…c = (Factor 1)(Factor 2) our “factor pair”
2. Identify which factor pair add together equal the “b” term
b = (Factor 1) + (Factor 2)
3. Write the BINOMIAL with the variable and the factors. Example: (x + 2)(x + 3)
Remember: (+)(+) = +
(+)(-) = (-)(-) = +
------------------------------------------------------------------Let’s try a few problems:
Factor x2 + 3x – 18
Step 1: The factors of 18 are (18)(-1) or (9)(-2) or (6)(-3)
** Since the “c” term is negative, our two numbers must have opposite signs!
** Since the “b” term is positive, the larger number must be positive!
Step 2: Which set of factors add to the “b” term?
(6)+(-3) = +3 , the “b” term
Step 3: (x + 6)(x – 3) are therefore the factors of this trinomial!
Solving Trinomials by Factoring and Applying the Zero Product Principle
The Zero Product Principle states:
“if we have the product of two Binomials set equal to zero, one or both must equal zero!”
Factor and Solve:
x2 + 2x =15
x2 + 2x – 15 = 0
Rearrange the terms with all parts on a single side.
Step 1: (15)(-1) or (5)(-3)
Step 2: (5) + (-3) = +2 our “b” term
Step 3: (x + 5)(x – 3) = 0
So (x + 5)(x – 3) = 0; therefore either (x + 5) = 0 or (x – 3) = 0
-5
-5
+3 +3
x=-5
or x = 3
To check our answers:
(-5)2 +(2)(-5) = 15
25 –10 = 15
15 = 15
(3)2 + (2)(3) = 15
9 + 6 = 15
15 = 15