* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download chapter 8
Survey
Document related concepts
Transcript
CHAPTER 8
SAMPLING METHODS AND THE CENTRAL LIMIT THEOREM
1.
See page 327 of the text.
3.
(a)
The value of population mean is
12 12 14 16
13.5
4
The value of population standard deviation is
12 13.5 12 13.5 14 13.5 16 13.5
2
2
2
4
1.6583
(b)
Each of the three data units selected can be any one of the four data units in the population.
Hence, the total number of possible samples of size 3 is 43 = 64.
(c)
Sample
Mean x
Sample
(12, 12)
(12, 12)
(12, 14)
(12, 16)
(12, 12)
(12, 12)
12
12
13
17
12
12
(12, 14)
(12, 16)
(14, 12)
(14, 12)
(14, 14)
(14, 16)
Mean x
13
14
13
13
14
15
Sample
Mean x
(16, 12)
(16, 12)
(16, 14)
(16, 16)
14
14
15
16
Sampling distribution of the sample mean X
Value of sample mean x
No. of Occurrences
12
4
13
4
14
5
15
2
16
1
5.
2
Probability
0.25
0.25
0.3125
0.125
0.0625
(d)
The mean and standard deviation of the sampling distribution are:
(e)
(f)
X 12 13.52 0.25 13 13.52 0.25 16 13.52 0.0625 1.1726
13.5 ;
X 13.5
The two are the same.
1.6583
Hence, X
1.6583;
X 1.1726
(a)
The population mean is :
X 120.25 130.25 160.0625 13.5
2
2 635
4
4
8-1
2
The population standard deviation is:
2 4 6 4 3 4 5 4
2
(b)
2
2
4
1.581
Sample means of all possible samples of size 2 using SRR
Sample Mean x Sample Mean x
Sample Mean x
(2, 2)
(2, 6)
(2, 3)
(2, 5)
(6, 2)
(6, 6)
(c)
2
2
4
2.5
3.5
4
6
(6, 3)
(6, 5)
(3, 2)
(3, 6)
(3, 3)
(3, 5)
4.5
5.5
2.5
4.5
3
4
(5, 2)
(5, 6)
(5, 3)
(5, 5)
3.5
5.5
4
5
Sampling distribution of the sample mean X
Sample mean x
No. of Occurrences
Probability
2
2.5
3
3.5
4
4.5
5
5.5
6
1/16 = 0.0625
2/16 = 0.125
1/16 = 0.0625
2/16 = 0.125
4/16 = 0.25
2/16 = 0.125
1/16 = 0.0625
2/16 = 0.125
1/16 = 0.0625
1
2
1
2
4
2
1
2
1
The mean of the sampling distribution of X is
X 2 0.0625 2.5 0.125
6 0.0625 4
The standard deviation of the sampling distribution X is
X
(d)
2 4 0.0625 2.5 4 0.125
2
6 4 0.0625 1.118
2
X 4 . Hence the mean of the sampling distribution equals the population mean.
1.581;
7.
2
X 1.118
1.581
2
Hence, X
2
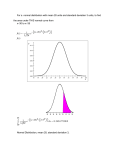
Since the sample size (n = 100) is large enough, it follows from the central limit theorem
that the distribution of X is approximately normal. Hence, distribution of
approximately standard normal.
(a)
If the claim is correct, then = 60. We know that = 12.
Let us find area under the normal to the right of 63.
8-2
X
is
n
z-value corresponding to 63 is z
63 60
2.5.
12 100
Thus, we want area under the Z-curve to the right of 2.5.
From the Z-table, the area under the Z-curve between 0 and 2.5 is 0.4938.
Hence, area under the curve to right of 2.5 is (0.5 – 0.4938) = 0.0062.
If the claim is correct, probability of getting a value of x greater than or equal to 63 is
0.0062. Hence, if we get a value of x = 63, it would be reasonable to conclude that the
claim is incorrect.
(b)
Let us find area under the normal to the left of 59.
If the claim is correct, then z-value corresponding to 59 is z
59 60
0.834.
12 100
Thus, we want area under the Z-curve to the left of –0.834.
From the Z-table, the area under the Z-curve between 0 and 0.834 is approximately 0.2978.
Hence, area under the curve to left of –0.834 is approximately (0.5 – 0.2978) = 0.2022.
If the claim is correct, then the probability of getting a value of x less than or equal to 59
is approximately 0.2022, which is fairly high. Thus, the sample data do not provide us any
evidence to doubt the claim.
X 68.2;
9.
X
n
9.2
1.4547
40
Since n is greater than 30, we can assume using the Central Limit Theorem that X is
approximately normally distributed.
So, X Normal(68.2, 1.4547)
(a)
We want area under the normal curve to the left of 65.
z-value corresponding to 65 is z
65 68.2
-2.2.
1.4547
Thus, we want area under the Z-curve to the left of –2.2.
From the Z-table, the area under the Z-curve between 0 and 2.2 is 0.4861.
Hence, area under the curve to left of –2.2 is (0.5 – 0.4861) = 0.0139.
Probability that the value of the sample mean will be less than 65 is approximately 0.0139.
(b)
We want area under the normal curve to the right of 72.
z-value corresponding to 72 is z
72 68.2
2.612 .
1.4547
Thus, we want area under the Z-curve to the right of 2.612.
From the Z-table, the area under the Z-curve between 0 and 2.612 is approximately 0.4955.
Hence, area under the curve to right of 2.2612 is approximately (0.5 – 0.4955) = 0.0045.
Probability that the value of the sample mean will be more than 72 is approximately
0.0045.
8-3
11.
The size of the population (rents of all apartments in Victoria) is very large. Hence, in this
case, SRN is almost same as SRR. Also, the sample size (n = 50) is large enough. Hence,
we shall approximate
X
by Z, the standard normal variable.
S n
Let us assume that the claim, that = $ 580/month, is correct. If x = 565 and s = 150,
then the corresponding z-value is z =
565 580
-0.707.
150 50
We want area under the Z-curve to the left of –0.707.
From the Z-table, the area under the Z-curve between 0 and 0.707 is approximately 0.2601.
Hence, area under the curve to left of –0.707 is approximately (0.5 – 0.2601) = 0.2399.
Thus, if the claim is correct, then the probability of getting a z-value as small as –0.707 is
approximately 0.2399, which is fairly high. The sample data, therefore, does not provide us
with sufficient information doubt the claim.
The distribution of X is given to be approximately normal. The ratio n/N = (50/400) is
greater than 0.05. Hence, we shall use finite correction factor.
Thus, if the manager’s claim is correct, then
13.
X 450 and X
60 350
N n
7.947.
n N 1
50 399
So, X Normal (450, 7.947).
Let us find the probability of getting a value of X greater than or equal to 470.
470 450
2.517 .
7.947
z-value corresponding to 470 is z
We want area under the Z-curve to the right of 2.517.
From the Z-table, the area under the Z-curve between 0 and 2.517 is approximately 0.4941.
Hence, area under the curve to right of 2.517 is approximately (0.5 – 0.4941) = 0.0059.
So, if the manager’s claim is correct, probability of getting a value of sample mean of 470
or higher is approximately 0.0059, which is fairly small. Since we obtained a value of
sample mean of 470, it is reasonable to conclude that the manager’s claim is incorrect.
15.
The population size is large. Hence SRN is almost same as SRR.
np = (200)(0.072) = 14.4 > 5, n (1- p) = 200 (0.928) = 185.6 > 5
Hence, we can assume that p̂ is approximately normally distributed with mean = 0.072
and standard deviation =
(a)
0.072(0.928)
0.0183
200
We want area under the normal curve to the right of 0.08.
z-value corresponding to 0.08 is z =
0.08 0.072
0.437
0.0183
Thus, we want area under the Z-curve to the right of 0.437.
From the Z-table, the area under the Z-curve between 0 and 0.437 is approximately 0.1689.
Hence, area under the curve to right of 0.437 is approximately (0.5 – 0.1689) = 0.3311.
(b)
If the Statistics Canada report is correct, probability that more than 8% the sampled
workers will be unemployed is 0.3311. This is a fairly large number.
8-4
Hence, the sample does not provide us with evidence against the Statistics Canada report.
We have insufficient evidence to doubt the report.
17.
In real life, it is difficult to implement SRR exactly. The following scheme will be a good
enough approximation to SRR scheme.
Most families in your city are likely to have one telephone number each (A few will have
more than one and a few will have none).
So, use your telephone directory and randomly choose ten pages using SRR and random
numbers. For each selected page, randomly choose a telephone number using a random
number.
19.
1. Destructive nature of the test. For example, testing life of battery.
2. Physically impossible to check all items. For example, measure weight of all the fish in a
lake.
3. Costly and time consuming to check all items. For example, collecting political opinion
of all the voters in Canada.
21.
23.
25.
A simple random sample would be appropriate, but this means the 720 pipes would have to
be numbered 0, 1, 2, …, 719. A more convenient method would be to (1) randomly select a
pipe from the first say, 20 pipes produced, and (2) select every 20th pipe produced
thereafter and measure its inside diameter. Thus, the sample would include about 36 PVC
pipes.
(a)
Starting with beginning of row 10, we get the following SRN sample:
048, 133, 224, 218, 217, 248, 195, 069, 186, 240.
(b)
250/10 = 25. Hence the sample, using systematic sampling is 17, 42, 67, 92, 117, 142, 167,
192, 217, 242.
(c)
Since the passengers normally board according to seat numbers, the sample will be
uniformly divided across seat numbers if systematic sampling is used. There is however a
possibility of sampling only windows customer or only aisle customers. This depends on
numbering of seats in the aircraft.
(d)
We could use cluster sampling by treating all the passengers seated in the same row as a
cluster. We could also use stratified sampling by dividing passengers into males and
females or into different age groups or into different fare classes.
(a)
Each of the selected data unit can be any one of the five data units in the population.
Hence, the total number of samples possible is 52 = 25.
(b)
Sample
Mean x Sample
Mean x
(2, 2)
(2, 3)
(2, 5)
(2, 3)
(2, 5)
(3, 2)
(3, 3)
2
2.5
3.5
2.5
3.5
2.5
3
4
5
2.5
3
4
3
4
(5, 3)
(5, 5)
(3, 2)
(3, 3)
(3, 5)
(3, 3)
(3, 5)
8-5
(3, 5)
(3, 3)
(3, 5)
(5, 2)
(5, 3)
(5, 5)
4
3
4
3.5
4
5
(5, 2)
(5, 3)
(5, 5)
(5, 3)
(5, 5)
Value of sample mean x
2
2.5
3
3.5
4
5
(c)
3.5
4
5
4
5
No. of Occurrences
1
4
4
4
8
4
Probability
0.04
0.16
0.16
0.16
0.32
0.16
The mean and standard deviation of the sampling distribution are:
X 2 0.04 2.5 0.16
5 0.16 3.6
2 3.6 0.04 2.5 3.6 0.16
X
2
2
5 3.6 0.16
2
= 0.8485.
The population mean and standard deviation are:
23535
3.6
5
2 3.6 3 3.6 5 3.6 3 3.6 5 3.6
2
27.
2
2
2
5
3.6 ;
X 3.6
1.2;
X 0.8485
2
1.2
The two are the same.
1.2
2
Hence, X
2
.
(a)
Each of the selected data unit can be any one of the six data units in the population. Hence,
the total number of samples possible is 64 = 1296.
(b)
Sample
(54, 54)
(54, 50)
(54, 52)
(54, 48)
(54, 50)
(54, 52)
(50, 54)
(50, 50)
(50, 52)
(50, 48)
(50, 50)
(50, 52)
Mean x
54
52
53
51
52
53
52
50
51
49
50
51
Sample
(52, 54)
(52, 50)
(52, 52)
(52, 48)
(52, 50)
(52, 52)
(48, 54)
(48, 50)
(48, 52)
(48, 48)
(48, 50)
(48, 52)
8-6
Mean x
53
51
52
50
51
52
51
49
50
48
49
50
Sample
(50, 54)
(50, 50)
(50, 52)
(50, 48)
(50, 50)
(50, 52)
(52, 54)
(52, 50)
(52, 52)
(52, 48)
(52, 50)
(52, 52)
Mean x
52
50
51
49
50
51
53
51
52
50
51
52
Value of sample mean x
48
49
50
51
52
53
54
(c)
No. of Occurrences
1
4
8
10
8
4
1
Probability
0.0278
0.1111
0.2222
0.2778
0.2222
0.1111
0.0278
The mean and standard deviation of the sampling distribution are:
X 48 0.0278 49 0.1111
X
54 0.0278 51
48 51 0.0278 49 51 0.1111
2
2
54 51 0.0278
2
= 1.354.
The population mean and standard deviation are:
54 50 52 48 50 52
51
6
54 51 50 51 52 1
2
51 ;
1.9149;
29.
(a)
2
2
52 51
6
X 51
2
1.9149
The two are the same.
X 1.354
1.9149
2
Hence, X
2
.
Since the population size is large, SRN is almost the same as SRR. Since the population
distribution is approximately normal, the distribution of sample means will be almost
normal, with mean 135 seconds and standard deviation
8
seconds.
40
8
1.2649
40
(b)
Standard error of the mean is
(c)
We want area under the normal curve to the right of 138.
z-value corresponding to 138 is z =
138 135
2.372
1.2649
Thus, we want area under the Z-curve to the right of 2.372.
From the Z-table, we find that the area under the Z-curve between 0 and 2.372 is
approximately 0.4911.
Hence, area under the curve to right of 2.372 is approximately (0.5 – 0.4911) = 0.0089.
Approximately 0.89 percent of the sample means will be greater than 138.
(d)
We want area under the normal curve to the right of 133.
8-7
z-value corresponding to 133 is z =
133 135
1.581
1.2649
Thus, we want area under the Z-curve to the right of –1.581.
From the Z-table, we find that the area under the Z-curve between 0 and 1.581 is
approximately 0.443.
Hence, area under the curve to right of –1.581 is approximately (0.5 + 0.443) = 0.943.
Approximately 94.3 percent of the sample means will be greater than 133.
(e)
31.
From part (c) and (d), we see that area under the normal curve between 133 and 135 (= )
is approximately 0.443 and area between 135 (= ) and 138 is approximately 0.4911. So,
the area under the curve between 133 and 138 is approximately (0.443 + 0.4911) = 0.9341.
The population size (number of people married in BC) is very large. Hence SRN is almost
the same as SRR. Hence,
X
is approximately a standard normal variable.
S n
We are given that = 28.8 and s = 2.5. Hence, z-value corresponding to 28 is z
=
28 28.8
2.48 .
2.5 60
From the Z-table, we find that the area under the Z-curve between 0 and 2.48 is 0.4934.
Hence, area under the curve to left of -2.48 is (0.5 - 0.4934) = 0.0066.
The probability is approximately 0.0066 that the value of sample mean will be less than
28.
33.
Population size (purchases by all the possible customers) is large enough. Hence SRN is
almost same as SRR.
n is large enough. Hence, we shall approximate
(a)
X
by Z.
S n
Let us assume that the claim that = 23.5 is correct.
z-value corresponding to x = 25 and s = 5 is z =
25 23.50
2.12
5 50
Probability that Z is at least 2.12 = approximately (0.5 – 0.483) = 0.017
Thus, if the claim is correct, probability of getting a z-value as large as 2.12 is very small
(= 0.017). Hence, if we get z-value = 2.12, it will be reasonable to conclude that the claim
is incorrect.
(b)
We know that probability that Z is in the interval (0 + 1.645) is 0.9.
6
1.3958
50
Hence “u” is approximately 1.645
35.
Sample size is large enough. Hence X is approximately normally distributed with mean =
947 and standard deviation = 205 60 = 26.465.
We want the probability that x is less than 900.
z-value corresponding to x = 900 is z =
8-8
900 947
1.776
205 60
Using the Z-table, we get the probability that Z is less than -1.776 is approximately (0.5 –
0.4621) = 0.0379
37.
(a)
For sheer physical convenience, we should use cluster sampling. We should randomly
select a few areas and collect data on sizes of all the farms in selected areas.
(b)
The population is large. So SRN is almost same as SRR. The sample size is large. So, we
can approximate
X
by Z.
S n
Approximate z-value corresponding to x = 560 and s = 180 is
560 608
2.67
180 100
From the Z-table, we get the probability that Z is less than or equal to –2.67 is (0.5 –
0.4962) = 0.0038
Since this probability is small, it would be reasonable to conclude that the average farm
size has decreased.
39.
41.
(a)
The sample, chosen using SRN and the given random numbers, will include the following
airlines:
{Frontier Airlines Inc., British Airways, Ryanair Holdings Inc., America West Holdings,
Air Canada Inc., Midway Airlines Corp.}
(b)
The data will vary according to the date on which you search the web.
(c)
Answer will vary according to the data.
(d)
N = 34, n = 6, N/n = 34/6 = 5.67. Hence k = 5.
The sample will include 4th, 9th, 14th, 19th, 24th and 29th airlines, which are {Alaska Air
Group Inc., China Eastern Airlines, Frontier Airlines Inc., Lan Chile S. A., Northwest
Airlines Corp., Trans World Airlines Inc.}
(a)
The population mean is = 1871.9 (see Microsoft Excel as well as Minitab outputs).
Minitab does not calculate population standard deviation. From Microsoft Excel output we
get = 652.5544.
MINITAB OUTPUT
Descriptive Statistics: C1
Variable
C1
N
55
Variable
C1
Minimum
526.0
Mean
1871.9
Median
1906.0
Maximum
3693.0
Q1
1478.0
TrMean
1849.9
Q3
2229.0
MEGASTAT OUTPUT
Descriptive statistics
count
55
mean
1,871.95
population sample variance 425,827.22
population standard deviation
652.55
8-9
StDev
658.6
SE Mean
88.8
(b)
If we assume that (i) distributions of snowfall during different winter days are identical and
independent and (ii) there has been no change in weather pattern during this 55 years
period, then by Central Limit Theorem, it would follow that the distribution of the total
snowfall during the winter days will be approximately normal. However, (i) it is generally
accepted that there has been a change in weather pattern in Halifax area during the last 40
years and (ii) distributions of snowfall during different winter days do not really seem to
be independent or identical.
Hence, Central Limit Theorem does not exactly apply. The final distribution may not be
normal.
(c)
The shape of the histogram is not exactly normal though it is not too non-normal either.
This is not inconsistent with expectation in part (b).
(d)
If a sample of size 30 is selected using SRR, then since n is large enough, the distribution
of X will be approximately normal with mean = 1871.9 and standard deviation
652.5544
119.1396 .
30
z-value corresponding to 2030 is z
2030 1871.9
1.327 .
119.1396
We want area under the Z-curve to the right of 1.327.
From the Z-table, area under the Z-curve between 0 and 1.327 is approximately 0.4075.
Hence area under the curve to the right of 1.327 is approximately (0.5 - 0.4075) = 0.0925.
43.
(e)
The answer will vary according to the sample obtained.
(a)
Using Microsoft Excel, we get the population standard deviation = 5.076689.
(b)
Select a sample of size 30 using SRN, as per the instructions given in the chapter. Repeat
this 50 times to get 50 samples. Find sample standard deviation for each sample and plot
histogram using instructions in Chapter 2. Answer will vary. Using central limit theorem,
one would expect the shape of the histogram to be approximately normal.
8-10