Download Jet Impact

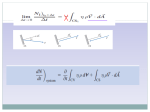
Last Rev.: 11 JUN 08
Jet Impact : MIME 3470
Page 1
Grading Sheet
~~~~~~~~~~~~~~
MIME 3470—Thermal Science Laboratory
~~~~~~~~~~~~~~
Experiment №. 6
JET IMPACT
Students’ Names / Section №
APPEARANCE, ORGANIZATION, ENGLISH, and GRAMMAR
MATHCAD
Ordered Data, Dimensions, Physical Properties
Calculations & Results Arrays—Include Velocity & Force %Diff
Required Plots
DISCUSSION OF RESULTS
Comment on Differences in Velocity & Force Between Nozzle & Target
When Can One Ignore Gravity in Bernoulli’s Equation?
Kline-McClintock Uncertainty
CONCLUSIONS
ORIGINAL DATASHEET
TOTAL
COMMENTS
d
GRADER—
POINTS
10
10
15
15
10
10
15
10
5
100
SCORE
TOTAL
Last Rev.: 11 JUN 08
Jet Impact : MIME 3470
Fy   m 2V2 sin  .
MIME 3470—Thermal Science Laboratory
~~~~~~~~~~~~~~
Experiment №. 6
(4)
Moreover, since the jet is flowing freely through air, it is
considered to be under constant pressure (i.e., atmospheric) at its
interface with the atmosphere. Therefore, it may be assumed that the
jet cross-sectional area is constant, A1 = A2. Now from Equation 1
m 1  m 2
FORCE ON VARIOUSLY SHAPED
OBJECTS DUE TO
JET IMPACT
(5)
1 A1V1  2 A2V2
and since the fluid is incompressible.
V1  V2 .
Therefore, Equations 2 and 3 become1
 V11  cos 
Fy  m 2V1 sin .
Fx  m
~~~~~~~~~~~~~~
LAB PARTNERS: NAME
NAME
NAME
SECTION
№
EXPERIMENT TIME/DATE:
Page 2
NAME
NAME
NAME
TIME, DATE
~~~~~~~~~~~~~~
OBJECTIVE—This experiment is a study in momentum transfer
(ergo, force transmitted) from a fluid to objects of various forms. In
particular, the study looks at the momentum transfer as a function of
the angle through which the fluid stream was deflected. By varying a
fluid stream’s deflection angle, up to twice the original momentum of
the stream can be transferred to the object.
INTRODUCTION—Over the years, engineers have found many
ways to utilize the impact force of fluids. For example, the Pelton
wheel has been used to make flour. Further, the impulse turbine is
still used in the first and also sometimes the second stage of a steam
turbine. Firemen make use of the kinetic energy stored in a jet to
extinguish fires in high-rise buildings. Many other applications of
fluid jets can be cited which reveals their technological importance.
This experiment is designed to study the force that can be imparted by
a jet of fluid on a surface diverting the flow.
(7)
EXPERIMENTAL PROCEDURE—The experimental apparatus
is that shown in Figure 2. The procedure detailed below is to be
performed on each of two different targets (vanes)—one a flat plate
and the other a hemispherical cup. That procedure is as follows:
Flat Plate Target
Hopper
Balance Bar
Jockey Balance Bar
x1 x2
0
Level
Indicator
y
Hemispherical
Cup Target
3L
L
Valve
Weighing Tank
(Hopper)
Hanger
with
5kg
Mass
x
Jockey Mass
Spring with Adjustable
Tension for
Leveling Balance
Beam w/ No Flow
Stop
y

F
(6)
P
Water Reservoir

Figure 1 — Impact Force Imparted by a Fluid Jet to a Body When
the Body Changes the Flow Direction of the Fluid
THEORY—A change in momentum of an object or a fluid is
always accompanied by an impulse force (impact force).
Consider a jet of fluid flowing steadily with a velocity V1 and a
mass flow rate m 1 . The jet impinges on a plate inclined at an angle 
to the direction of the flow. From a mass balance, the same amount of
liquid impinging on the plate must also leave the plate; thus,
.
(1)
m 1  m 2  m
Force is the time derivative of momentum, mv, where m is the
mass impacting on the plate and v is the velocity of impact. Thus,
d mv
dv
dm
F

m
v
 m v .
(2)
dt
dt
dt

0
As there is no
acceleration
 just a change
in mass flow
From a momentum balance the sum of external forces equals the
change in momentum

 F  m v out  m v in .
Hence, for the x-direction of the system in Figure 1,
1V1  m
 2V2 cos   m
 V1  V2 cos 
(3)
Fx  m
and in the y-direction
Figure 2—Experimental Apparatus
1
Think about what is happening before blindly applying these equations.
Last Rev.: 11 JUN 08
Jet Impact : MIME 3470
1. The experiment is set up such that the balance beam is horizontal
when the upward force of the water impinging on the target is
balanced by the downward force of the jockey weight. This
means that the balance beam and the target are considered to be
weightless. To achieve this weightless estate, the beam is leveled
by changing the tension of the adjusting spring shown in the
figure when no water is flowing and for the jockey mass at x1 =
0. This must be done for each target used as they are not expected
to have the same weight.
2. In taking data, it would be convenient to have round values of
x2 such as 180mm as to 178mm. Thus, the water flow was
turned on full force, the jockey weight positioned to the
nearest round value, and the water flow backed off just enough
to level the balance bar. (It is easier to adjust the water flow
for a given position of the jockey weight as to trying to
position of the jockey weight for a specified flow of water.).
3. At the left of the schematic is shown a weight hanger. It is
quite heavy in its own right—even before additional weight is
added. The discharge hopper (weighing tank) is emptied until
the weight hanger drops under its own weight. The drain plug
at the bottom of the tank is reinserted and the tank begins to
fill. At the point in filling the tank when the tank balance bar
and weight hanger rise up and hit a stop, a stop watch is
started. Directly after starting the watch, 5kg of additional
weight is added to the weight hanger. As the discharge tank
continues to fill, eventually enough weight of water is
achieved to outweigh the 5kg of additional weight that was
added. This causes the tank balance beam to rise up against the
stop again at which time the stop watch is halted.
4. The ratio of moment arms on either side of the fulcrum of the
tank balance beam is 3:1 such that 5kg of additional weight is
balanced by 15kg of water. The flow rate is then 15kg of water
during the time that the stop watch was running
Page 3
5. Decreasing values of x2 are then laid in and flow reduced
accordingly.
6. Data was taken for a total of six (approximately evenly
spaced) positions of the jockey weight.
7. Perform these steps for each of the targets (flat plate and
hemispherical cup).
In the report:
1. On one graph, plot for both targets the experimental force vs.
the theoretical force. Here, the experimental force is that
calculated from the jockey weight and its position. The
theoretical force is that calculated from the water flow rate. In
determining the theoretical force, the velocity at the target
must be used. The distance from the nozzle to the target (if the
jockey weight balance beam has been leveled prior to flowing
water) is y = 35mm.
2. On one graph, plot for both targets the experimental force vs
the jet velocity at the target. On this plot, also plot twice the
flat-plate experimental force vs. velocity at the target.
3. In the calculations, determine the percent difference in both the
velocity and the theoretical force exerted at the target due to the
distance between the nozzle tip and the target. In the discussion,
comment on the differences in velocity and force between nozzle
and target. Answer the question: when does gravitational deceleration as described by Bernoulli’s relation become important and
when may it be neglected?
4. Finally, considering that the only experimental error is caused by
the measuring scale on the jockey weight balance bar, find the
uncertainty in determining the experimental force imparted on
the target using the Kline-McClintock method. Comment on this
in the discussion. There is a separate downloadable file
describing the Kline-McClintock method.
Last Rev.: 11 JUN 08
Jet Impact : MIME 3470
Page 4
Ordered Data, Calculations, & Results
BA SIC DIMENSIONS, MA SSES, & PHYSICA L PROPERTIES
Jock ey Weigh Mass:
Nozzle Diameter:
Nozzle-to-Target Distance:
Piv ot-to-Nozzle Distance:
Tank A rm/Hanger A rm Ratio :
Mass Placed on Hanger:
Mass of Water in Hopper:
A cceleration of Grav ity :
Density of Water:
i  1  6
FLA T PLA TE DA TA : (subscript
"pl" stands for flat PLate)
HEMISHERICA L CUP DA TA :(subscript
"cup" stands for hemispherical CUP)
Last Rev.: 11 JUN 08
Jet Impact : MIME 3470
DISCUSSION OF RESULTS
Comment on the differences in velocity and force between nozzle
and target.
Answer
With respect to the first question, when does gravitational
deceleration as described by Bernoulli’s relation become
important and when may it be neglected?
Answer
Considering that the only experimental error is caused by the
measuring scale on the jockey weight balance bar, find the
uncertainty in determining the experimental force imparted on
the vane using the Kline-McClintock method.
Answer
CONCLUSIONS
Page 5
Last Rev.: 11 JUN 08
Jet Impact : MIME 3470
APPENDIX A—DATA SHEET
Page 6
FOR JET IMPACT
Time/Date:
___________________
Lab Partners:
_______________________
_______________________
_______________________
_______________________
_______________________
_______________________
Mass of Jockey Weight
_____________
Nozzle Diameter
_____________
Distance from Nozzle to Target, y
_____________
Distance from Pivot to Jet Center, x1
_____________
Mass Used on Weight Hanger
_____________
Ratio of (Tank Lever Arm)
to (Weight Hanger Lever Arm)
_____________
Finest Graduation on Balance Bar
_____________
Run
FLAT PLATE TARGET
Distance of Jockey
Time to Fill
Mass from Jet
Tank,
Center, x2
s
cm
Run
1
1
2
2
3
3
4
4
5
5
6
6
HEMISPHERICAL TARGET
Distance of Jockey
Time to Fill
Mass from Jet
Tank,
Center, x2
s
cm