Download Algebra III/Trigonometry - Garnet Valley School District

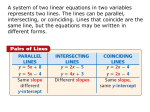
Algebra III/Trigonometry Midterm Review
List the three forms of linear equations that we have studied.
1.) Point-Slope Form =
2.) Slope-Intercept Form =
3.) Standard Form =
4.) Define what the x and y intercept is.
5.) Describe the relationship between the slopes of parallel lines and perpendicular lines.
6.) Describe what you are finding when you find a solution to a system of equations with two variables.
7.) Define what it means if a system of equations is consistent, inconsistent, or dependent.
8.) List the laws of exponents that we have studied so far.
List the three properties of Logs we have studied so far.
9.) Log(a*b) =
Log(a/b) =
Log ab =
10.) Given the equation 2x –3y –16 = 0, find a point that satisfies the equation and a point that does not satisfy the equations. You
should demonstrate both. (4 points)
Given the following scenario, answer the questions below.
When you dive off a 3-meter diving board, time and your position in relation to the water’s surface are related to each other. (Hint:
Time is almost always which variable? 2 points each)
11.) Name the independent variable.
12.) Name the dependent variable.
13.) Name the possible domain.
14.) Name the possible range.
Graph each of the following. (3 points each)
17.) y = 5x – 2
18.) –3y + 5x – 6 = 0
Write the equation of the line described in Slope-Intercept form.
19.) Has y-intercept of 10 and slope of –3/5.
20.) Contains the point (8, -2) and has slope of ½.
21.) Contains the points (4, -6) and (2, 8).
22.) Contains the point (2, -1) and is parallel to the line 6x +3y = 9
Write the equation of the line described in Slope-Intercept form. (4 points each)
23.) Contains the point (9,-2) and is perpendicular to the line 3x + 4y = -8
24.) Your electrical bill varies linearly with the number of kilowatts you use in your home. You notice one month you used 90kilowatt hours and the charge was $65. The next month you were charged $110 for 200-kilowatt hours.
a.
Write the particular equation of this function expressing cost in terms of usage.
b.
What is the price of 250-kilowatt hours?
c.
If your bill was $800, what was your usage?
Given the function f(x) = 2x2 + 11x + 9 answer the following questions.
27.) Find the value of f(-2).
29.) Find the x-intercepts.
28.) Find the value of f(5).
30.) Square the binomial (5x – 9)2.
31.) Write the given equation in vertex form.
y = 2x2 – 8x + 24
Solve the following equation for x.
32.) –7x2 + 2x + 3 = -9x2 + 7x
33.) Solve x2 – 6x +13 = 0.
34.) Write the conjugate of 5 –3i.
35.) Graph the parabola y = -3(x + 2)2 – 4 by finding the requested information.
a.) vertex =
b.) y-intercept =
c.) symmetric point =
Factor and solve the following.
36.) x2 – 9x + 20 = 0
37.) 5x2 – 8x – 4 =0
Solve the following systems of equations
38.) x – 3y = -9
x + 2y = -4
39.) 2x – 5y = 26
3x + 4y = 16
40.) 3x – y = 10
2x + 5y = 1
41.) 3x – 2y + 5z = -17
2x + 4y – 3z = 29
5x – 6y – 7z = 7
42.) Multiply (5 – 7 i)(4 + 3 i). Simplify completely.
43.) Draw a graph of 2x – 6y + 4z = 12. Be sure to write the traces. (4 points)
45.) Plot the solution to the system of inequalities. (5 points)
x<3
y > -2
x+y<5
x + y > -3
When a football is punted, the function h(x) = -16t2 + 40t + 4 models the relationship between the height of the football and the time
elapsed in seconds. Use this model to answer the following questions. (2 points each)
46.) How far above the ground was the football when it was punted?
47.) How long did it take the football to reach the maximum height?
48.) What was the maximum height of the ball?
49.) How long did it take the football to return to the ground?
Solve the following. The more work you show the more partial credit you will receive. (3 points each)
50.) 7x = 63
51.) 4*62x = 50
Assume that log 2 = .301, log 3 = .477 and log 10 = 1. Use the properties of logs to solve the following. (3 points each)
52.) log 360
53.) log 12
Solve the following. The more work you show, the more partial credit you will receive. (3 points each)
54.) log256 32 = x
55.) logx 81 = 4/3
56.) log32 x = 7/5
57.) log125 1/25 = x
Simplify the following. (2 points each)
58.) (4x13y11)5 =
59.) 7x15
21x-8
60.) (115.1)(113.2) =
61.) 9510/9508 =