* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download File
Golden ratio wikipedia , lookup
Dessin d'enfant wikipedia , lookup
Steinitz's theorem wikipedia , lookup
Trigonometric functions wikipedia , lookup
Rational trigonometry wikipedia , lookup
Atiyah–Singer index theorem wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Riemann–Roch theorem wikipedia , lookup
Noether's theorem wikipedia , lookup
Euclidean geometry wikipedia , lookup
History of trigonometry wikipedia , lookup
Brouwer fixed-point theorem wikipedia , lookup
Integer triangle wikipedia , lookup
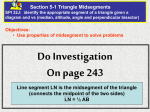
Name: _________________________________________________________ Date: ______________ Per: _______ LC Math 2 Adv – Triangle Midsegment Theorem (LT 11) Triangle Midsegment Theorem: The segment that joins the midpoints of two sides of a triangle: (1) is parallel to the third side. (2) is half as long as the third side. Use the envelope of statements and reasons to complete Part 1 of the proof of the Triangle Midsegment Theorem. Then copy your proof into the space below. ̅̅̅̅. Given: D is the midpoint of 𝐴𝐵 E is the midpoint of ̅̅̅̅ 𝐴𝐶 . Prove: ̅̅̅̅ 𝐷𝐸 ‖ ̅̅̅̅ 𝐵𝐶 Statement Reason D is the midpoint of ̅̅̅̅ 𝐴𝐵 . ̅̅̅̅ . E is the midpoint of 𝐴𝐶 Given 𝐴𝐷 + 𝐷𝐵 = 𝐴𝐵 𝐴𝐸 + 𝐸𝐶 = 𝐴𝐶 Segment Addition Postulate 𝐴𝐷 = 𝐷𝐵 ; 𝐴𝐸 = 𝐸𝐶 Definition of midpoint 2𝐴𝐷 = 𝐴𝐵 2𝐴𝐸 = 𝐴𝐶 Substitution 𝐴𝐵 𝐴𝐶 = 𝐴𝐷 𝐴𝐸 Property of Proportions ∠𝐴 ≅ ∠𝐴 Reflexive Property of Congruence ∆𝐴𝐵𝐶~∆𝐴𝐷𝐸 SAS Similarity ∠𝐴𝐵𝐶 ≅ ∠𝐴𝐷𝐸 Corresponding Angles of Similar Triangles are Congruent ̅̅̅̅ ‖𝐷𝐸 ̅̅̅̅ 𝐵𝐶 Corresponding Angles ≅ Parallel Lines Name: _________________________________________________________ Date: ______________ Per: _______ LC Math 2 Adv – Triangle Midsegment Theorem (LT 11) Triangle Midsegment Theorem: The segment that joins the midpoints of two sides of a triangle: (1) is parallel to the third side. (2) is half as long as the third side. Use the skeleton proof below to fill in the missing statements and reasons for the Triangle Midsegment Theorem. Given: D is the midpoint of ̅̅̅̅ 𝐴𝐵. ̅̅̅̅ . E is the midpoint of 𝐴𝐶 ̅̅̅̅ ̅̅̅̅ ‖ 𝐵𝐶 Prove: 𝐷𝐸 Statement Reason Given 𝐴𝐷 + 𝐷𝐵 = 𝐴𝐵 𝐴𝐸 + 𝐸𝐶 = 𝐴𝐶 Definition of midpoint Substitution 𝐴𝐵 𝐴𝐶 = 𝐴𝐷 𝐴𝐸 Reflexive Property of Congruence ∆𝐴𝐵𝐶~∆𝐴𝐷𝐸 Corresponding Angles of Similar Triangles are Congruent Name: _________________________________________________________ Date: ______________ Per: _______ LC Math 2 Adv – Triangle Midsegment Theorem (LT 11) Triangle Midsegment Theorem: The segment that joins the midpoints of two sides of a triangle: (1) is parallel to the third side. (2) is half as long as the third side. Prove Part 1 of the Triangle Midsegment Theorem in the space below. ̅̅̅̅. Given: D is the midpoint of 𝐴𝐵 E is the midpoint of ̅̅̅̅ 𝐴𝐶 . Prove: ̅̅̅̅ 𝐷𝐸 ‖ ̅̅̅̅ 𝐵𝐶 Statement Reason Triangle Midsegment Theorem: The segment that joins the midpoints of two sides of a triangle: (1) is parallel to the third side. (2) is half as long as the third side. Using any conclusions from the proof of the first part of this theorem, continue your proof to show that the second part of the theorem must be true. 1 Prove: 𝐷𝐸 = 2 𝐵𝐶 Statement Reason