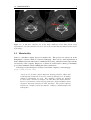
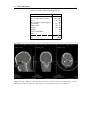
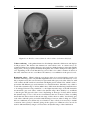
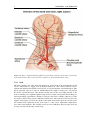
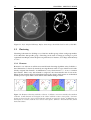
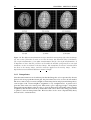
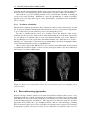
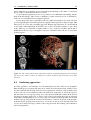
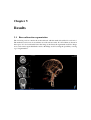
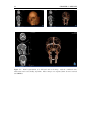
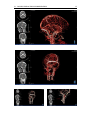
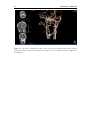
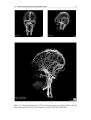
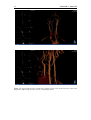
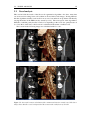
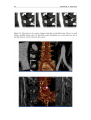
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Blood vessel segmentation for neck and head computed tomography angiography Anders Hedblom
Hold-And-Modify wikipedia , lookup
Indexed color wikipedia , lookup
Medical imaging wikipedia , lookup
Edge detection wikipedia , lookup
Stereoscopy wikipedia , lookup
Stereo display wikipedia , lookup
Image editing wikipedia , lookup
Spatial anti-aliasing wikipedia , lookup
LiU-ITN-TEK-A-13/056-SE Blood vessel segmentation for neck and head computed tomography angiography Anders Hedblom 2013-10-11 Department of Science and Technology Linköping University SE- 6 0 1 7 4 No r r köping , Sw ed en Institutionen för teknik och naturvetenskap Linköpings universitet 6 0 1 7 4 No r r köping LiU-ITN-TEK-A-13/056-SE Blood vessel segmentation for neck and head computed tomography angiography Examensarbete utfört i Medieteknik vid Tekniska högskolan vid Linköpings universitet Anders Hedblom Handledare Gunnar Läthén Examinator Jonas Unger Norrköping 2013-10-11 Upphovsrätt Detta dokument hålls tillgängligt på Internet – eller dess framtida ersättare – under en längre tid från publiceringsdatum under förutsättning att inga extraordinära omständigheter uppstår. Tillgång till dokumentet innebär tillstånd för var och en att läsa, ladda ner, skriva ut enstaka kopior för enskilt bruk och att använda det oförändrat för ickekommersiell forskning och för undervisning. Överföring av upphovsrätten vid en senare tidpunkt kan inte upphäva detta tillstånd. All annan användning av dokumentet kräver upphovsmannens medgivande. För att garantera äktheten, säkerheten och tillgängligheten finns det lösningar av teknisk och administrativ art. Upphovsmannens ideella rätt innefattar rätt att bli nämnd som upphovsman i den omfattning som god sed kräver vid användning av dokumentet på ovan beskrivna sätt samt skydd mot att dokumentet ändras eller presenteras i sådan form eller i sådant sammanhang som är kränkande för upphovsmannens litterära eller konstnärliga anseende eller egenart. För ytterligare information om Linköping University Electronic Press se förlagets hemsida http://www.ep.liu.se/ Copyright The publishers will keep this document online on the Internet - or its possible replacement - for a considerable time from the date of publication barring exceptional circumstances. The online availability of the document implies a permanent permission for anyone to read, to download, to print out single copies for your own use and to use it unchanged for any non-commercial research and educational purpose. Subsequent transfers of copyright cannot revoke this permission. All other uses of the document are conditional on the consent of the copyright owner. The publisher has taken technical and administrative measures to assure authenticity, security and accessibility. According to intellectual property law the author has the right to be mentioned when his/her work is accessed as described above and to be protected against infringement. For additional information about the Linköping University Electronic Press and its procedures for publication and for assurance of document integrity, please refer to its WWW home page: http://www.ep.liu.se/ © Anders Hedblom ITN, Norrköping October 31, 2013 Blood vessel segmentation for neck and head computed tomography angiography A MASTER THESIS IN COMPUTER TECHNOLOGY Author: Anders Hedblom Examiner: Jonas Unger Supervisors: Gunnar Läthén Chunliang Wang Aron Ernvik Erik Edespong [email protected] [email protected] [email protected] Abstract Medical imaging has become an invaluable tool over the last decades. The development from two dimensional X-ray images to the possibility of creating three dimensional representations of the body has helped significantly when it comes to detecting diseases. Today, the most common cause of death is vascular diseases that can lead to a heart attack or a stroke. The problem is that both happen very instantaneously and can be difficult to predict. Angiography allows for examination of the blood vessels in the body without having to undergo surgery. The body is scanned, with for instance a computed tomography scanner, and can then be viewed in 3D. All the tissues in the body will be displayed with different intensities, depending on their densities. Blood vessels do not stand out well from their surrounding tissues and have to be injected with a contrast enhancing fluid before the scan. However, this leads to some complications, mainly an intensity overlap between blood vessels and bone. This means that, to get a clear view of the blood vessels, an image segmentation has to be done. Many methods for doing so have been presented over the years, but none capable of doing segmentation of all the vessels in the head and neck simultaneously. This thesis presents tests and discussions evaluating different methods for doing automatic or semi automatic blood vessel segmentation on single CT data volumes of the head and neck. The two approaches being closest to accomplish this are a bone subtracting registration process, and a more advanced region growing combined with morphology. The results hint that the former approach does not give segmentations that are good enough to fit this task with todays hardware. The latter method is more likely to be useful as its results are good but requires on the other hand far more user interaction during the segmentation process. There will always be a tradeoff between automation, quality and speed. Most of the test were done in MeVisLab – an open source software for medical image processing. Acknowledgments It has been a long journey, reaching the end of my education. Long and challenging, but never did I doubt that I was going in the right direction – I have learned a lot and created friendships that will last for life. I want to thank Sectra for giving me the opportunity to work with them. Many thanks to all my supervisors who have helped me a lot with ideas and feedback. Especially I want to thank Chunliang Wang who gave me much of his time and knowledge about different segmentation methods, also checking in from time to time to see how I was doing. Finally, I want to thank all my friends and family for supporting me and believing in me when I didn’t. It means a lot. Glossary Artery/Arteries Blood vessels, transporting oxygen rich blood from the heart to the rest of the body. The only time when arteries are low on oxygen is when going from the heart to the lungs (Pulmonary arteries). Bit depth The number of bits used to store a pixel/data. Higher bit depth gives greater accuracy and higher dynamic intensity range. BSCTA Bone Subtraction Computed Tomography Angiography is a hardware based way of segmenting and displaying blood vessels. It requires two CT data sets – one with contrast agent injected and one without. Thus, it exposes the body to more radiation than CTA. Capillary/Capillaries Small vessels that connect arteries and veins. Responsible for the interchange of chemicals between blood and tissue. CT Computed Tomography is a technique to reconstruct an image presentation of the body by using several X-ray projections. CTA Computed Tomography Angiography – visualization of the blood vessels where the data is captured from one or several CT scans, having a contrast agent injected into the vessels. Dual-energy Scan By using two different x-ray wavelengths during a CT scan, it is possible to capture two tissue responses instead of one. Different tissues respond differently to the wavelength change, which makes it possible to distinguish vessels from bone easier. Hemorrhage A rupture of a blood vessel, causing blood to leak out in surrounding tissue. HU Hounsfield Units. Used to measure x-ray attenuation in tissue. ITK The Insight Segmentation and Registration Toolkit (ITK) is an open-source, cross-platform library for image analysis and processing. Lumen In angiography, lumen is the hollow inside of a blood vessel. Some vascular diseases cause the lumen to become thinner. Metric A definition of distance between two points in a metric space or between two data sets. MIP Maximum Intensity Projection (MIP) is a rule for how the voxels will be displayed during volume rendering. As the name hints, it takes the voxel with the maximum value along each ray and assigns this to its belonging screen pixel. MPR Multiplanar Reconstruction is when a 2D image is created by first stacking all axial slices from a CT-scan, to build a data volume, and then cut a new slice in any given plane. MRI Magnetic Resonance Imaging. An imaging modality which uses nuclear magnetic resonance to image the body in 2D or 3D. Pixel Picture element Plaque Substance that can build up on the inner walls of blood vessels. It consists mainly of fat, cholesterol, calcium.Plaque both narrows the lumen and makes the vessels more rigid, which both make the vessel less healthy. ROI Region of Interest Vein/Veins Blood vessels, transporting carbon dioxide rich blood, back to the heart. The only time veins are rich on oxygen is when going from the lungs to the heart (Pulmonary veins). Voxel Volume element X-ray Electromagnetic radiation where the wavelength is between 0.01 and 0.1 nanometers. Contents 1 Introduction 1.1 Problem description . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1.2 Main facility . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 Background 2.1 Preliminaries . . . . . . 2.2 Anatomy overview . . . 2.2.1 Neck . . . . . . 2.2.2 Head . . . . . . 2.2.3 Bone and marrow 2.2.4 Blood vessels . . 2.3 Common diseases . . . . 2.3.1 Stenosis . . . . . 2.3.2 Aneurysm . . . . 2.3.3 Stroke . . . . . . 2.4 Medical imaging . . . . 2.4.1 CT . . . . . . . 2.4.2 MRI . . . . . . . 2.5 Image segmentation . . . 3 1 2 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 4 7 8 9 9 9 10 10 10 10 10 11 11 12 Previous work 3.1 Thresholding . . . . . . . . . . . . . . . . 3.2 Clustering . . . . . . . . . . . . . . . . . . 3.2.1 K-means . . . . . . . . . . . . . . 3.3 Morphological operations . . . . . . . . . . 3.4 Edge enhancements . . . . . . . . . . . . . 3.4.1 Gradient calculations . . . . . . . . 3.5 Region growing . . . . . . . . . . . . . . . 3.6 Active contour model . . . . . . . . . . . . 3.7 Shape extraction . . . . . . . . . . . . . . . 3.7.1 Vesselness . . . . . . . . . . . . . 3.8 Registration . . . . . . . . . . . . . . . . . 3.8.1 Transforms . . . . . . . . . . . . . 3.8.2 Interpolators . . . . . . . . . . . . 3.8.3 Metrics . . . . . . . . . . . . . . . 3.8.4 Optimizers . . . . . . . . . . . . . 3.8.5 Doing registration in multiple steps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 13 14 14 15 17 17 18 19 19 20 20 21 22 23 23 24 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 Method and implementation 4.1 Software . . . . . . . . . . . . 4.1.1 MeVisLab . . . . . . . 4.1.2 Matlab . . . . . . . . 4.1.3 Elastix . . . . . . . . 4.2 Vessel finding approaches . . . 4.2.1 Region growing . . . . 4.2.2 Centerline tracking . . 4.2.3 Vesselness calculation 4.3 Bone subtracting approaches . 4.3.1 Gradient based method 4.3.2 Bone registration . . . 4.4 Combining approaches . . . . 4.5 Vessel analysis . . . . . . . . . . . . . . . . . . . . . 25 25 25 25 26 26 26 26 27 27 28 28 29 31 5 Results 5.1 Bone subtraction segmentation . . . . . . . . . . . . . . . . . . . . . . . . . . 5.2 Vessel analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5.3 Evaluation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 33 39 42 6 Conclusion 6.1 Discussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6.2 Future work . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 43 44 Bibliography . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46 List of Figures 1.1 A CT slice, showing one of the many challenges when doing blood vessel segmentation – the left vertebral vessel is so close to the vertebra that they almost meld together in the image. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 2.1 The different orthographic projections of a CT volume in sagittal (left), coronal (middle) and axial (right) views. The yellow cross marks the same voxel in all views. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A 2D slice extracted from the whole volume of a human skull (left). . . . . . . . Histogram of a CT image. The dots are key points for adjustment of dynamic range and opacity for those HU values. This adjustable histogram is a part of the 3D engine, integrated into MeVisLab. . . . . . . . . . . . . . . . . . . . . Source: http://antranik.org/blood-vessels/. Basic structure of the main vessels in the neck and head area. The vessels with lower opacity are located behind bone tissue. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Source: http://en.wikipedia.org/wiki/File:Blood vessels.svg. The basic anatomy of blood vessels. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2.2 2.3 2.4 2.5 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 Left: Original CT image. Right: Same image, thresholded with a value of 500 HU. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . K-means clustering with three clusters. 1) Cluster centers are initialized as random elements. 2) All elements are assigned to the cluster with the nearest center point. 3) Center points are moved to the center of all elements assigned to respective cluster. 4) Elements are reassigned to a cluster, with the new closest center point. 5) Done! All elements have found their final cluster. . . . . . . . . Source: http://en.wikipedia.org/wiki/File:Dilation.png. Dilation of the dark-blue, with a circular structure element, region results in the union of the dark-blue and light-blue region. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Source: http://en.wikipedia.org/wiki/File:Erosion.png. Erosion of the dark-blue region, with a circular structure element, results in the light-blue region. . . . Source: http://en.wikipedia.org/wiki/File:Opening.png. Opening of the dark-blue region, with a circular structure element, results in light-blue region. . . . . . Source: http://en.wikipedia.org/wiki/File:Closing.png. Closing of the dark-blue region, with a circular structure element, results in the union of the dark-blue and light-blue region. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . The gradient operator applied to the surface in (a). The result is a vector field (b). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . The principles of region growing. A seed point is initialized as the first active element (blue). All active elements check for non-labeled pixels/voxels in its neighborhood (here, in a 8-connected fashion). If a checked pixel agrees with the chosen intensity threshold it will be updated as an active pixel/voxel. All previous active pixels/voxels become labeled as part of the region (green). . . . 5 6 7 8 9 14 14 15 16 16 17 18 19 3.9 The different transformations trying to match the moving image (b) to the fixed image (a). An overlay grid makes it easier to see how the image has deformed with (c) translation, (d) a rigid transformation, (e) an affine transformation and (f) a non-rigid transformation. It is important to notice that the grid does not resemble the movable grid points for a non-rigid transform, as they are defined on the fixed image. The transforms are always calculated from the fixed to the moving image, and then inversely applied on the moving image. Source: http://elastix.isi.uu.nl/download/elastix manual v4.6.pdf . . . . . . . . . . . . 3.10 One dimensional example of interpolations of the discrete data points in a), where b) is nearest-neighbor, c) is linear interpolation and d) is polynomial interpolation with a sixth degree polynomial. . . . . . . . . . . . . . . . . . . 4.1 4.2 4.3 5.1 5.2 5.3 5.4 5.5 5.6 5.7 Blood vessel segmentation where the vessel intensities have been amplified with a vesselness filter. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . The result of doing bone subtraction with the registration approach. Even though this was a nice data set, there are still pieces of bone fragments left, and some vessel data removed. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Centerline algorithm in Sectra’s internal tool VRTTest. Two mouse clicks are used to place start and stop for the centerline. This can be done either in 3D or 2D. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Final segmentation of a CT head and neck image, with the combined bone subtraction and vessel finding algorithm. These images are captured from Sectra’s internal tool VRTTest. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . The same segmentation shown with voxels of lower HU included and excluded respectively. This is good if only either the cerebral vessels or carotid vessels are supposed to be examined. . . . . . . . . . . . . . . . . . . . . . . . . . . . Final segmentation of a CT head and neck image, viewed from behind, obliquely downwards and from the side. The 3D image is rendered with MIP in MeVisLab. Segmentation of the carotid and vertebral vessels. The zoomed in figure shows that the patient suffers from stenosis near the carotid bifurcation. . . . . . . . Successful contour calculation of the common and interior carotid vessel. The lower image shows that the vessel is diagnosed with stenosis with a risk factor of 53-65% . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Showing how the contour changes along the carotid bifurcation. There is a small distance (middle image) where the algorithm cannot distinguish two vessels from one, due to the high intensity voxels in between the vessels. . . . . . . . . More results showing that the algorithm is capable of segmenting: large, noisy vessels (top); vessels that are very small and close to another vessel (second); highly calcified vessels (bottom two). . . . . . . . . . . . . . . . . . . . . . . 22 23 27 29 31 34 36 37 38 39 40 41 Chapter 1 Introduction Medical imaging is an important and quickly growing subject. Due to the fact that vascular diseases are a major cause of death, it is important to be able to study the vessels for more knowledge and to examine the patients to detect any of these diseases before they become too severe. Angiography is the process of visualizing the lumen, i.e. the inside, of blood vessels. This can be done by intravenously injecting a contrast agent into the patient, followed by a computed tomography scan. It allows the doctors to get a view of the body, presented as a volume of x-ray data. The contrast agent is used to make the vessels stand out from the surrounding softer tissue. However, this inevitably leads to another problem. The density of bone tissue varies so much that some parts will overlap with the blood vessels, intensity-wise, and therefore obscure the vessels during visualization. This means that it is necessary to do a vessel segmentation before visualizing the data. Vessel segmentation is a common technique and is therefore well documented, for instance seen in A review of vessel extraction techniques and algorithms [1], presented by Kirbas et al in 2004, and later in Survey of 3d image segmentation methods [2], by O. Wiejadi in 2007. However, most of the methods could still be improved. First of all, there are ways to do angiography with a very good view of the vessels, having almost as good as no bone left in the image at all. But these methods expose the body to higher doses of radiation. They can also be time consuming and therefore cost more money. Some methods allow for very good segmentation of certain vessels, such as the common carotid vessels and the carotid bifurcation, as presented by O. Cuisenaire et al [3] and M. Freiman et al [4]. Even though this is a common location for defects, it would be more efficient if all vessels in a region, in this case the head and neck, could be visualized simultaneously. However, this involves several problems since the structure and placement of bone and blood vessels are different in the head compared to the neck. This is the report for my master thesis in media and computer technology, which was done at Sectra during spring 2013. It discusses different methods for doing automatic or semi automatic blood vessel segmentation on single CT data volumes of the neck and head. These data sets are all captured with contrast agent injected into the blood vessels. The structure of this report is as follows: A short introduction to the problem and the purpose of this project is the part you are reading now. The second part contains some background of medical imaging and anatomy. Following is a chapter with previous work to give the reader the knowledge necessary to follow the evaluation of the different evaluated segmentation approaches. After that, the tested methods are presented, followed by a chapter containing the achieved results. Everything is then summed up in the conclusion part. 2 CHAPTER 1. INTRODUCTION 1.1 Problem description The main issue when trying to segment contrast agent filled vessels is the intensity overlap that occurs between vessels and bones. The density of different skeleton parts varies heavily throughout the body. In Computed Tomography Images (CTI) the HU values for bone and cartilage stretch from around 200 to 3000, whereas the contrast enhanced blood vessels have values between 100 and 500 HU. This means that the two cannot easily be separated with thresholding techniques. When the vessels are visible, the images will also show the softest part of the skeleton. Furthermore, the thin gap between bone and vessels, in some areas, makes the task even more complicated. The carotid vessels, going from neck to head, pass through the Temporal bone via the Carotid canal, where the vessel is completely enclosed by bone with a separation of less than a millimeter. For most CT scanners, the image resolution is too coarse (commonly >1 mm spacing between slices) to capture a distance of this size, thus making the rim of the vessel blend into the bone. Smaller vessels also closely stretch along the surface of the occipital bone. This hampers most segmentation methods. However, it is highly important to be able to completely remove the bones while keeping the vessels for visual inspection. By doing so, symptoms for pathologies, like stenosis, plaque or aneurysms, can be detected more effortlessly. It is possible to solve the problem by taking two different images of the body, as with the BSCTA method, for instance used by Garatam van Andel et al [5], and later further compared to normal CTA by D. Morhard et al [6]. Another way is to use dual-energy scans, presented and discussed by M. van Straten et al [7]. The MRI also gives good representation of vessels without too much image processing. However, with today’s computer power it is, for several reasons, favorable to solve the problem software-oriented. This gives a good compromise of using little radiation and not taking too long to carry through. The main motivation for not using techniques as BSCTA or dual-energy is the amount of radiation that the body is exposed to. The purpose of this project is to come up with an idea how to do automatic or semi automatic blood vessel segmentation good enough to be used by physicians, not using more than a single CT scan. The ultimate goal would be an algorithm that allows the user to press a ”segmentation” button and nothing but the blood vessels would be visualized on-screen. Vessel segmentation can be done with two main approaches: 1. Locating all the blood vessels with an appropriate method and visualizing them. This can, for instance, be done by ray casting the original vessel data or by creating a mesh around the edges of the vessels. The problem with this approach is that the number of vessels is huge. Their structure varies a lot, going from the neck area up to the brain. The placement and structure of the vessels also differs a lot from person to person, which can make the results more uncertain. 2. Subtracting all, or as much as possible, of the obscuring bone tissue. Finding the bone allows for a segmentation of the vessels by masking away the bone. When this is done, the contrast filled vessels can easily be separated from surrounding lower intensity tissue by using thresholding. Large parts of the scull can be located quickly with several methods, since they have defined structure and are not adjacent to any important vessels. However, as mentioned, bone varies a lot in density and can resemble blood vessels in some areas in the lower skull region and parts of the vertebras. Each approach allows for different methods to be used, though nothing says they cannot be combined for a more accurate result. 1.2. MAIN FACILITY 3 Figure 1.1: A CT slice, showing one of the many challenges when doing blood vessel segmentation – the left vertebral vessel is so close to the vertebra that they almost meld together in the image. 1.2 Main facility Sectra is a Swedish company that was founded 1978. This project was carried out at the headquarters of Sectra, which is located in Linköping. There are two main departments at Sectra, Medical Systems and Secure Communication Systems, where the former represents the vast majority of the company. Employees of Sectra are well known for having a remarkably good contact with their clients, fulfilling the clients actual needs. Following is a brief description of Sectra, found at the company’s own homepage: http://www.sectra.com/ “Sectra is one of today’s major diagnostic imaging providers. More than 1,400 hospitals worldwide use Sectra’s system, performing over 50 million radiology examinations per year. The company’s systems are installed in most major countries in Europe, the Far East and North America. Sectra’s core business is delivering top-of-the-line, high-availability, robust enterprise diagnostic imaging for 24/7 operation. The product offering includes for example systems for film-free radiology, mammography and orthopedics.” Chapter 2 Background In order to fully understand the rest of the report, the process and the challenges that occur during blood vessel segmentation, this chapter provides a basic background of medical imaging and other subjects that are relevant to this project. 2.1 Preliminaries Notations: Throughout this report, if nothing else is stated, scalars are written as normal lowercase symbols (x), scalar fields as normal upper case symbols (X), vectors as bold lowercase symbols (x) and vector fields as bold uppercase symbols (X). Hounsfield Units (HU): HU is the standard reference scale used for measuring x-ray image intensities. It builds on the fact that denser material absorbs more radiation than soft materials and leaves less photons to hit the printing plate. X-ray images are usually inverted to make dense material, such as bone, have high intensities, thus appear bright in the final image. The Hounsfield unit is defined such that the radiodensity of distilled water (at STP - Standard Temperature and Pressure) is equal to zero HU, and the radiodensity of air (at STP) is equal to −1000 HU, seen in equation 2.1. HU = 1000 µx − µwater µwater (2.1) where µx represents the linear attenuation coefficient in a specific voxel x and µwater is the linear attenuation coefficient for water. Approximate HU values for different tissues can be found in the table 2.1, [8]. Note that, these values change depending on the wavelength of the x-rays. This is taken advantage of when using dual energy CT-scanners, which however is outside the scope of this project. Volume Data: In the same way as an image can be represented with a discrete two-dimensional pixel grid, volume data can be described with a three-dimensional voxel grid. From the grid, it is possible to reconstruct a 2D slice, as seen in figure 2.1 and 2.2. 2.1. PRELIMINARIES 5 Table 2.1: Table of HU for different tissues Tissue Bone Blood (with contrast agent) Liver Blood (without contrast agent) Gray matter White matter Muscle Kidney Cerebrospinal fluid Water Fat Air HU 200 – 3000 100 – 500 40 – 60 40 37 – 45 20 – 30 10 – 40 30 15 0 -50 – (-100) -1000 Figure 2.1: The different orthographic projections of a CT volume in sagittal (left), coronal (middle) and axial (right) views. The yellow cross marks the same voxel in all views. 6 CHAPTER 2. BACKGROUND Figure 2.2: A 2D slice extracted from the whole volume of a human skull (left). Volume rendering is the gathered name for all techniques that take a 3D data set and displays its 2D projection. The discrete data elements are often called voxels. A common way to do volume rendering is ray casting, where rays are cast from a defined camera position, through the image plane (one ray per pixel) and finally through the data volume. Each pixel is then given a color depending on the voxels that their ray passed. The color could for instance be based on the value of the first non-zero voxel that is encountered, or a combination of the passed voxels. Remapping values: When looking at x-ray images, there is no need for having several color channels of the image, since only the HU magnitude needs to be stored in each and every voxel. On a computer screen, this can obviously be represented with a gray scale value. However, with a CT scanner, the HU variation is measured with higher precision than 8 bits, which is used to present the 256 different gray scale intensities on a standard monitor. Often the x-ray volume is stored with a dynamic range of 12 bits (4096 values). This means that the image intensities have to be remapped before being visualized, i.e., the higher dynamic range of the HU intensities are turned into gray scale values, with a lower dynamic range. Most suitably is to recalibrate so that air gives the grayscale value of zero. Depending on what type of tissue will be studied, the dynamic range of one to 255 can be concentrated in the area of interest. Thus, everything denser than the densest tissue in the chosen range, will be shown as white. Just showing gray scale values with full opacity is feasible with 2D-images, however, when looking at a volume, this is not sufficient (we would mostly see a black box, due to all air). It is necessary to include a variation of the opacity, for instance giving air the opacity zero. Different colors can also be used for different intensity ranges to increase the total dynamic range of the visualization. 2.2. ANATOMY OVERVIEW 7 Figure 2.3: Histogram of a CT image. The dots are key points for adjustment of dynamic range and opacity for those HU values. This adjustable histogram is a part of the 3D engine, integrated into MeVisLab. 2.2 Anatomy overview In this section the basic vessel structure is outlined, in order to get an overview of the case. Since the brain requires a lot of oxygen to function properly, the arteries and veins leading there have to be thick. From mid-neck area and upwards, duplicates of the vessels are located on left and right side, even though their shape might differ somewhat. 8 CHAPTER 2. BACKGROUND Figure 2.4: Source: http://antranik.org/blood-vessels/. Basic structure of the main vessels in the neck and head area. The vessels with lower opacity are located behind bone tissue. 2.2.1 Neck The neck contains some of the most important blood vessels in the body, including the carotid vessels. Their task is to supply most of the head with blood. The common carotid vessel is split into the internal and external carotid vessels, at a point called the carotid bifurcation. This part is especially exposed to stenosis, which makes it the culprit to many cases of decreased blood flow towards the head. The internal carotid vessel is the one leading inwards to the brain. It actually passes right through the temporal bone via the carotid canal, thus making it a critical part during segmentation. Finally it connects to the Circle of Willis, where most of the blood passes before being sent into different cerebral areas. The external carotid vessel mostly supplies facial organs as well as the outside of the skull. In the neck region, the carotid vessels are normally well separated from any bone tissue, i.e., they can be segmented comparatively easy with several methods. The vertebral vessels are more difficult as they are partly enclosed by every cervical vertebra they extend along. 10 CHAPTER 2. BACKGROUND During angiography, the lumen of the vessels are the most important part. The border of the lumen will also be the border of contrast agent that is injected into the blood, and is therefore the most visible part of the vessel during visualization. The most common reason for blood flow degradation is narrowing of the lumen. 2.3 Common diseases The following section describes some of the most common vessel problems. They are together the main cause to do an angiography. 2.3.1 Stenosis Stenosis is a narrowing of tubular organs, such as blood vessels and tracheal parts, leading to decreased effectiveness or full loss of function. Arterial stenosis is caused by the build-up of plaque on the inner walls of the vessels. When this happens on the carotid vessels, major parts of the blood flow can be blocked. Symptoms are rarely noticed until the stenosis is at a severe stage and a clot forms, creating a transient ischemic attack (a mini-stroke). Since stenosis narrows the actual lumen of a blood vessel, it can be detected with medical imaging, for instance by doing a CT angiography. 2.3.2 Aneurysm Aneurysms are caused by a weakening of the blood vessel walls and appears as a balloon-like shape on its side. The aneurysm can grow to a size where it breaks and causes hemorrhage. If this happens in the cerebral area, where aneurysms often occur, the consequences can be severe. Larger aneurysms can easily be detected during an angiography. 2.3.3 Stroke A stroke is more a critical state than a disease – it is the result of a sudden loss of blood flow to the brain. Smaller strokes can be temporary and disappear within minutes, others can be permanent if no medical treatment is given. This could lead to major damage to the brain or in worst case, death. A stroke is caused either by a blockage of a blood vessel or hemorrhage. 2.4 Medical imaging The use of medical imaging has indeed grown vastly over the last years. It occupies a big part of computational research and constantly pushes the development of visualization and image processing forward, hand in hand with hardware development. In 1895, Wilhelm Röntgen discovered the x-ray. It was such a huge discovery that he was awarded with the first ever Nobel Prize in Physics. X-rays have been used ever since, in particular to visualize and analyze the inside of objects. Over the years, other methods for doing so have been invented, due to the hostile nature of radiation for the human body: magnetic resonance imaging and ultra sound, just to mention a few. The purpose of medical imaging is to create visualizations of living tissue, either for scientific research or clinical procedures, to better be able to analyze and diagnose diseases. Having the ability to do so saves a lot of time and money, not to mention that the accuracy of a diagnose increases. This is an important factor before, for instance, making the decision to do a surgery. Tomography is a technique that allows for creation of two-dimensional slices of the body. Each slice is represented as an image, where the pixels hold a transformation of the HU-value at 2.4. MEDICAL IMAGING 11 that position of the body. Since the image has a limited resolution, the value can either be based on the mean HU-value over the whole pixel area, or just the center value. When many slices are stacked, they create a volume representation of the body, a voxel grid. In most cases, this grid is not isotropically shaped, seeing that the spacing between slices not necessarily needs to be the same as the pixel spacing for every slice. Therefore, the grid might have to be resampled in order to get a non-distorted representation of the scanned body, before any image processing is done. Being able to study blood vessels, and prevent these diseases, is one of the most useful aspects of medical imaging. It is an indispensable tool for our healthcare and will be so even more in the future. As previously mentioned, ultrasound can be used for medical imaging, thoroughly discussed in the master thesis of Per Mattson and Andreas Eriksson [9]. However, when trying to visualize blood vessels, the two most common techniques are CT and MRI. 2.4.1 CT Computed tomography angiography There are many ways to get an inner view of the body without the need to physically examining it. Computed tomography is one of them and uses x-rays to scan the body. The difference from using normal x-ray imaging is that the body is scanned from different directions. The advantage of doing so is that it gives the possibility to create a 3D representation of the scanned area. This data can be processed in software to give a good view of any type of body tissue. CT scans are especially good at reproducing well defined images for bones and other harder tissue like cartilage, that x-rays have difficulty passing. Softer tissue like muscles or the brain are more clearly seen with magnetic resonance imaging (MRI). Bone subtraction computed tomography angiography Bone subtraction computed tomography angiography (BSCTA) allows for subtraction of bone during visualization, without much image processing. The patient is scanned twice in the same position: one time in normal condition and one time with contrast agent injected into the vascular system. The vessels can then, after registration (see section 3.8), be visualized separately by subtracting the first image from the second. There are however some drawbacks of doing so. Since two images have to be taken, the patient will suffer from twice as much radiation, compared to only doing a single scan. Furthermore, it can be inconvenient for the patient having to lie completely still for an extended time. 2.4.2 MRI Magnetic Resonance Imaging (MRI) is a newer way to create three-dimensional representations of the body. Instead of using x-rays to scan the body, very strong magnetic fields are used to orient the hydrogen atoms in a specific way. When the magnetic field is released, the atoms will return to their original orientation, thus loosing energy. The energy is turned into radio waves, which can be collected and turned into an image. For this reason, the MRI method is, as far as we know today, harmless to living tissue. Since this project only handles images from CT scans, MRI will not be further explained in this report. But it is still important to mention why MRI is not always used instead of CT. First of all, since MRI scanners are relatively new, they are generally more expensive than CT scanners. They also do not produce results with as good resolution as the CT scanners. A CT procedure can be done in a matter of seconds (∼30 – 60 sec), whereas doing a MRI scan takes several minutes (∼20 – 40 min). During this time, it is essential that the patient lies completely 12 CHAPTER 2. BACKGROUND still, which is not comfortable for everyone. Finally, CT and MRI produce images that differ a lot from one another. CT images are far more useful when looking at dense tissue, such as bone. MRI is more appropriate when looking at softer tissue, such as the brain [10]. 2.5 Image segmentation Image segmentation involves the process of partitioning image data into multiple sets of pixels/voxels. In other words, every pixel/voxel is assigned a label/value, where those with the same label/value belong to the same segment. There are a vast number of methods for doing image segmentation – thresholding, clustering, region growing and edge detection, just to mention a few – and they can be applied to varying problems: detection of pores in wood [11] for instance. Some of them can be used for doing blood vessel segmentation and are discussed in this report. The reason for doing segmentation is in most cases to get a different view on the image, mostly creating a more comprehensible representation of the original, making it easier to analyze. For this project, the whole problem consists of coming up with a good way to segment blood vessels from other tissues. If succeeding to do so, the final segmentation can be used to mask away obscuring tissue, primarily bone, to make it easier for the doctors to examine the vessels. But where many images can be easily segmented using, for instance colors, the segmentation task faced here is far more tricky. Chapter 3 Previous work 3.1 Thresholding Thresholding is a technique used for partitioning an image with respect to its intensity values. This is one of the easiest ways to do segmentation. Most often, the result is a binary mask where all the values that below the threshold are set to zero, and the ones greater than the threshold are set to one. If using two thresholds, the value one is often assigned to the intensities that lie within the two thresholds, and zero to the rest. Though it is possible to use an arbitrary number of thresholds, it is not that useful, as it requires the result to be handled differently than a mask. There are automated ways to decide which threshold values are going to be used for a particular image, where the most known is Otsu’s method. The basic idea is to search for a threshold that minimizes the variance within the segmentation. K. Zhao et al [12] also propose a method to automatically find thresholds for CT bone-subtraction. However, the approach is based on the fact that they have two images – with and without contrast fluid injected into the vessels. Even though thresholding is fast and easy to use, the method has some limitations. Sometimes a threshold value works well for one part of the image, but poorly for the rest. In the case of CT images, the problem is that different types of tissue can be very similar. It is thus difficult to decide one threshold value that does not include too much or too little of the wanted segment. The intensity overlap between bone and blood vessels results in this complication. 14 CHAPTER 3. PREVIOUS WORK Figure 3.1: Left: Original CT image. Right: Same image, thresholded with a value of 500 HU. 3.2 Clustering Clustering is the name for dividing a set of data into smaller groups, where each group member is best fitted into that specific group. Clustering can be used for image processing as a pixel segmentation technique, where the pixels are partitioned, for instance, according to their intensity or color. 3.2.1 K-means K-means is one of the most well-known centroid based clustering algorithms today. It divides n data elements into k clusters by iteratively moving the mean value for every cluster based on the i already assigned data elements. At initialization, every cluster mean kmean is set to a random data element. Then, every data element is assigned to the cluster that has the closest mean. When all data elements have been distributed among the clusters, their means are recalculated and the process repeats. This is done until no data element changes cluster. Figure 3.2: K-means clustering with three clusters. 1) Cluster centers are initialized as random elements. 2) All elements are assigned to the cluster with the nearest center point. 3) Center points are moved to the center of all elements assigned to respective cluster. 4) Elements are reassigned to a cluster, with the new closest center point. 5) Done! All elements have found their final cluster. 3.6. ACTIVE CONTOUR MODEL 19 Figure 3.8: The principles of region growing. A seed point is initialized as the first active element (blue). All active elements check for non-labeled pixels/voxels in its neighborhood (here, in a 8-connected fashion). If a checked pixel agrees with the chosen intensity threshold it will be updated as an active pixel/voxel. All previous active pixels/voxels become labeled as part of the region (green). 3.6 Active contour model Active contour model, also known as snakes, is a technique proposed by Kass et. al. [14], to outline the contour of an object. This is done by minimizing the energy of a spline, constrained by external and internal forces. These pull the contour towards features in the image, edges for instance, and lock the contour in place when the designated shape has converged. The total ∗ snake energy, Esnake , for a contour with n points, can be expressed as ∗ Esnake = Z 1 Esnake (v(s)) ds = 0 Z 1 (Einternal (v(s)) + Eexternal (v(s))) ds (3.6) 0 Eexternal = Eimage + Econ (3.7) where vi = (xi , yi ) and i = 0...n − 1. Eexternal is the external energy, Eimage is the energy based on the image values, Econ is the additional constraints energy given by the user and Einternal is the internal energy. The external energy reacts to the image intensities and additional constraints set by the user. The energy is minimized when a strong edge is found, i.e., the gradient is maximized. The internal energy is based on the current shape of the spline. Hard bends on the spline create more energy than smooth shapes, forcing the spline to straight out, a bit similar to a rubber band, which has a minimal internal energy when taking a perfect circular shape. An active contour model can be used to do image segmentation, by finding the edges of regions. S. Grosskopf et al [15] show how they can segment a vessel contour by using an adaptive and self-learning version of the active contour model. 3.7 Shape extraction Since blood vessels are more or less cylindrically shaped, they can be found by measuring how similar the local surrounding of each voxel is to a cylinder. Now, it is important to remember that blood vessels are not the only cylindrically shaped structures in the body. Tissues, such as tendons, bones and cartilage are all likely to show up in the result as well. So what approach is necessary to discover cylindrical shapes? It is a fact that the cross section of a cylinder is a circle. But there is also the fact that the cross section does not change 20 CHAPTER 3. PREVIOUS WORK much lengthwise. If these two features are satisfied, it is plausible to say that the shape is a cylinder. 3.7.1 Vesselness Vesselness calculation is based on the idea of looking at the eigenvalues of the Hessian matrix for every voxel in the image. The Hessian matrix can be derived by calculating the second-order partial derivatives of a function. Consequently, in three dimensions, the Hessian matrix, H(f ) is given by equation 3.8. 2 2 2 ∂ f 2 ∂∂x2 f H(f ) = ∂y∂x ∂2f ∂z∂x ∂ f ∂x∂y ∂2f ∂y 2 ∂2f ∂z∂y ∂ f ∂x∂z ∂2f ∂y∂z ∂2f ∂z 2 (3.8) where f (x, y, z) in this case gives the voxel intensities. With the eigenvalues, λ1 > λ2 > λ3 , a bright vessel on a darker background can be detected if the following condition is fulfilled: λ1 ≈ 0 and 0 >> λ2 ≈ λ3 . This states that in one direction around the voxel, the intensity change is near to zero, which would match the direction of the vessel. It also states that in the two other orthogonal directions, the intensity varies a lot, and approximately equally, which would match the near-circle shaped cross-section of the vessel. The more closely a voxel can be compared to this condition, the more likely it is that it belongs to a vessel shaped structure. R. Marcin [16] uses and describes this approach to find vessel structures in the body. 3.8 Registration Registration is the process of trying to spatially match a data set to another. In most cases, this is done on two-dimensional images, but can be done on volumetric data sets, meshes and more. It is a proven tool for medical imaging and can, for instance, be used to analyze sets of images. So how can this be used for blood vessel segmentation? Trying to match a bunch of blood vessels to the vessels of an arbitrary patient, to mask away the surrounding tissue, would be a next to impossible task. The vessels are numerous, relatively small compared to the image resolution and differ a lot in shape and size from person to person. A better approach would be to find the skeleton since the bone tissue is much more similar between different persons. Furthermore, a final registration of the bone does not have to be as accurate as a vessel registration, since removing too much/little bone will in most cases not affect any vessels at all. As mentioned previously however, some areas like the cervical vertebrae will still cause some problems due to close proximity of bone and vessels. In order to match a moving image Im(x) to a fixed image If(x), a designated transform T(x) is needed. T(x) can be any given transform: rigid, affine or completely non-rigid. Deriving the optimal transform is a non-trivial task that comes down to minimizing the difference between the two images, after the transform has been applied, such as showed in equation 3.9. T̂ = arg minC(IF (x), IM (T (x))) T (3.9) where T̂ is the optimal transform, x is an element that belong to the fixed image domain ΩF and C is a cost function that measures the difference between the fixed image and the transformed moving image. Solving such a minimizing problem computationally is an iterative process of optimizing the transform and measuring the error after it has been applied. Depending on what the user wants to accomplish, a set of parameters must be specified. These 3.8. REGISTRATION 21 include the type of transform that will be used, the optimizing algorithm, the cost function, the number of allowed iterations, stopping conditions, interpolation method, metric type, grid spacing in case of a non-rigid transformation, etc. 3.8.1 Transforms For all the following transforms, T is the transform on a data element position (in this case voxel position) x, with the input parameter vector µ Translation: Translation of an image is the pure movement of all pixels/voxels in one specific direction. The image is not allowed to rotate or transform in any way that does not keep the isometry of the image to itself. This is the simplest transformation that can be done. Translation is described as Tµ (x) = x + t (3.10) where t is the translation vector. Rigid: A rigid transform allows rotation in addition to translation. However, it does not allow any scaling or stretching of the image data. A rigid transform can be described as Tµ (x) = R(x − c) + t + c (3.11) where t, once again is the translation vector, R is the rotation matrix and c is the vector to the center of rotation. Affine: The affine transform extends the rigid transform by also allowing scaling and skewing. During an affine transformation, all straight lines before the transformation are kept straight afterwards. The affine transform is a good way to start a registration procedure. It can make a good line-up of two images so that only small adjustments remain to be done. The transform is described as Tµ (x) = A(x − c) + t + c (3.12) with the same notation as for the rigid transform, except that R is now replaced with the affine rotation matrix A that has no restrictions. Non-rigid: A registration is mostly finalized with a non-rigid transform, where B-splines are often used to parametrize it. The image is divided into a grid with a set spacing. Each point on the grid can move more or less independently from the others. The higher resolution of the grid, the less restricted is the transform, but a too high resolution can also lead to bad transformations and of course longer computation time. A non-rigid transform is not suited to match images that are differently rotated and scaled, but only to make finer adjustments. Therefore it is essential to apply a good base transform first. A non-rigid transform made with B-splines can be described as X 3 x − xk (3.13) pk β Tµ (x) = x + σ xk ∈Nx where xk is a movable point on the grid, the set N contains all of these grid points, β 3 (x) is the B-spline polynomial, pk is a vector containing all coefficients for the polynomial, and σ is the spacing between the grid points. 22 CHAPTER 3. PREVIOUS WORK Figure 3.9: The different transformations trying to match the moving image (b) to the fixed image (a). An overlay grid makes it easier to see how the image has deformed with (c) translation, (d) a rigid transformation, (e) an affine transformation and (f) a non-rigid transformation. It is important to notice that the grid does not resemble the movable grid points for a non-rigid transform, as they are defined on the fixed image. The transforms are always calculated from the fixed to the moving image, and then inversely applied on the moving image. Source: http://elastix.isi.uu.nl/download/elastix manual v4.6.pdf 3.8.2 Interpolators Since the transformations can be arbitrary, but the final image has to be represented by discrete pixels/voxels along a predefined static grid, the pixel values have to be set via a chosen method. The most common ways are nearest-neighbor, linear interpolation and polynomial interpolation, seen in figure 3.10. Nearest-neighbor assignment is very straightforward. A pixel/voxel is given the same value as its nearest pixel. This tends to give rough jagged edges. Using linear interpolation means that the value in point p is given by the nearest surrounding values, linearly weighted by their distance from the p. Even better result can be achieved by using polynomials or splines to derive an interpolated value. However, these are also more computationally heavy and can lead to over/under-shots. 3.8. REGISTRATION 23 Figure 3.10: One dimensional example of interpolations of the discrete data points in a), where b) is nearest-neighbor, c) is linear interpolation and d) is polynomial interpolation with a sixth degree polynomial. 3.8.3 Metrics The cost function, C in 3.9, returns a value based on a metric, used to measure the difference between the two images, i.e. a way of saying if the transformation was successful or not. The choice of metric is important and balances accuracy and computation time. An example of metric is the sum of squared differences. Sum of Squared Differences (SSD) is a common way to measure similarity in data sets. Every transformed data element, or here voxel, is compared to its original. The difference is squared and summed to all other voxel differences. The result is divided with the total number of voxels to give the mean error, as seen in equation 3.14. SSD(IF , IM ) = X 1 (IF (x) − IM (T (x)))2 | ΩF | (3.14) xi ∈ΩF where F and M are indications for fixed and moving image I, respectively, Ω is the set of all voxels, x is the voxel position and T is the transform that was applied to it. 3.8.4 Optimizers Optimizers are used to derive how best the parameters should be changed in order to minimize the difference (given by the metric) between the fixed and the moving image. A common 24 CHAPTER 3. PREVIOUS WORK optimizer is the gradient descent method [17], which checks for the largest minimization of the metric and keeps transforming in that direction. 3.8.5 Doing registration in multiple steps Combining transforms In order to get a good result from the registration process it is often necessary to combine different types of transformations. If the moving image looks a lot different from the fixed image, it might not be possible to get a valid result at all, but a good start is to do some basic transforms, such as rigid and affine transform. This will help a great deal getting the moving image matched against the fixed image. This can then be followed up with a B-spline transform, to adjust the details. If the rigid/affine transformation was poor, it is not likely to get good results here either – in some cases the outcome can be far worse than the input. Multiple resolutions Using multiple resolutions helps a lot when registering complex images. This basically means that the registration is done repeatedly, first with a very coarse resolution, followed up by higher and higher detail level. The coarse images can either be down sampled or blurred versions of the original images. This implies that there will be less struggle for the optimizer to move the image around in the beginning, but still being able to match the details in the final steps. An example of down sampling can be to have the resolution halved for each step. That is, if using four different resolutions, the first registration will be done on images that have been down sampled to one eighth of the original resolution, then one fourth, then one half and finally with the true resolution. Multi-Atlas Hortense A. Kirisli et al [18] take the registration one step further by using an atlas of fixed images. The moving image is registered towards all images in the atlas and basically, the best matched result is used. This does indeed improve the possibilities of successful registrations but is very time consuming. Five images in the atlas means five times more computation. Chapter 4 Method and implementation This chapter briefly describes the softwares that were used during the project and the different methods that were tested for blood vessel segmentation. 4.1 Software 4.1.1 MeVisLab MeVisLab is an open source software that has been invaluable for prototyping during this project. MeVisLab allowed for testing of many different approaches to vessel segmentation, that would not have been possible otherwise for such a time limited period. It can be quickly described none better than by quoting the developers from the home page: “MeVisLab represents a platform for image processing research and development with a focus on medical imaging. It allows fast integration and testing of new algorithms and the development of application prototypes that can be used in clinical environments. MeVisLab includes advanced medical imaging modules for segmentation, registration, volumetry, and quantitative morphological and functional analysis. Several clinical prototypes have been realized on the basis of MeVisLab, including software assistants for neuro-imaging, dynamic image analysis, surgery planning, and vessel analysis. The implementation of MeVisLab makes use of a number of well known third-party libraries and technologies, most importantly the application framework Qt, the visualization and interaction toolkit Open Inventor, the scripting language Python, and the graphics standard OpenGL. MeVisLab has originally been created and developed by Fraunhofer MEVIS (formerly MeVis Research). Since the transfer of MeVisLab to MeVis Medical Solutions in 2008, the further development and advancement of MeVisLab as well as the communication with the MeVisLab users community is pursued as a joint effort between MeVis Medical Solutions and Fraunhofer MEVIS. A part of the modules contained in the MeVisLab distribution are directly contributed by Fraunhofer MEVIS.” MeVisLab’s user friendly node based system makes it very comprehensible, even for beginners. Many of the existing implemented algorithms are taken directly from ITK, which is convenient since it allows the user to keep these algorithms when leaving the prototyping state. 4.1.2 Matlab Matlab is a cross-platform environment created by MathWorks, used for numerical computing. Matlab is really good for solving image processing tasks, many thanks to the Image Processing Toolbox and image viewing capabilities. For this project, it was used for prototyping, mainly during the vessel analysis part, see section 4.5. The program language is very easy to use and 26 CHAPTER 4. METHOD AND IMPLEMENTATION allows for quick import of images into matrices – most functions in Matlab are matrix based. Thanks to Matlab’s matrix based syntax, many operations can be done on multiple data elements without the necessity of writing for-loops. However, where Matlab shines with its versatility, it lacks in computational speed that other languages provide, such as C++. Therefore, Matlab code is often ported to another language when a working prototype has been developed. 4.1.3 Elastix Elastix is a toolbox for rigid and non-rigid registration, and was used for all registration tests during this project. The description from the developers reads as follows: “Elastix is open source software, based on the well-known Insight Segmentation and Registration Toolkit (ITK). The software consists of a collection of algorithms that are commonly used to solve (medical) image registration problems. The modular design of Elastix allows the user to quickly configure, test, and compare different registration methods for a specific application. A command-line interface enables automated processing of large numbers of data sets, by means of scripting.” Elastix is easy to get started with and has a well documented users manual. 4.2 Vessel finding approaches The vessel finding approaches involves trying to find the blood vessels themselves and sorting all other voxels away. 4.2.1 Region growing One of the most intuitive ways to find all vessels would be to locate one or several places in the image where most of the blood must pass, and search outwards from there. If the scan includes some of the chest area, the aorta is a good point to start. Otherwise, one point in each common carotid vessel should be enough. If region growing could be executed here, the problem would be more or less solved. However, as previously discussed this is not entirely possible. Due to the intensity overlap and close proximity of bone, the region growing will leak out and include bone parts such as vertebrae and parts of the scull. In some few cases, where the vessels are better separated from bone structure, it might be possible to minimize leakage to a point where it is no longer critical. But by doing so, it is likely to have included too little of the vessels themselves. The region growing method works very well though, if the only goal is to strip the skull bone. It is possible to place a seed point at arbitrary locations inside the brain, and then region grow the brain with an upper threshold set just so that none of the skull bone is included. If there are any vessels in the head that were excluded as well, they can be selected by some closing operations. Still, the threshold parameter is very difficult to adjust. This method was tested early on, both in Matlab and MeVisLab, and was abandoned not long after. It requires a lot of parameter tweaking and is, by far, not robust enough on its own. 4.2.2 Centerline tracking The centerline tracking was tested with the Tubular Tracking [19] node in MeVisLab. This algorithm takes a seed point from where it tries to track the centerline of a tube shaped structure, such as a blood vessel, by fitting a cylindrical kernel. The kernel is always moved bi-directional 4.3. BONE SUBTRACTING APPROACHES 27 along the already found centerline, and the rotation is tested in several steps. The algorithm also allows the user to test multiple hypothesis, which makes it possible to find vessel branching. This method is good for tracking uniform vessels, but lacks the versatility of finding all vessels in the neck and head. Furthermore, since the algorithm has to check for multiple hypotheses in every single time step, in order to find branches, it quickly becomes an immense task to compute. 4.2.3 Vesselness calculation MeVisLab has a built-in algorithm for direct calculation of the vesselness in the image. It could also be done by manually calculating the Hessian matrix for every voxel and use its eigenvalues to get a scalar field as a result. Both ways were tested during this project. In order to actually find the vessels, it is essential to know the diameter of the vessels. Generally, the blood vessels in the neck are much thicker than those in the head. Even if the two are split up, it is still impossible to set an exact diameter that fits every vessel. Therefore, the algorithm has to be run several times with different kernel sizes. This takes a lot of time – filtering a 5123 image with a 73 kernel involves around 46 billion operations, though this number can be reduced drastically by using a rough ROI mask. The vesselness approach is difficult to use on its own since it inevitably finds other tissue that is cylindrically structured. Figure 4.1 shows an early result given with a coarse bone subtraction followed by a vesselness enhancement. Figure 4.1: Blood vessel segmentation where the vessel intensities have been amplified with a vesselness filter. 4.3 Bone subtracting approaches Instead of trying to find the actual vessels in the neck and head, which we have seen is a very challenging task, they could be visualized if all obscuring bone would be removed. This would mean that no left-over tissue would overlap the vessels intensity-wise and could easily be hidden by thresholding during the visualization. This approach was embraced when the described approaches above turned out to give insufficient results. The two main advantages of finding the bone instead of the vessels is, first of all, that bone structure varies less than vessel structure from patient to patient, and second of all, it does not affect the vessel data the same way. For 28 CHAPTER 4. METHOD AND IMPLEMENTATION instance, this approach is much more reasonable for segmenting the vessels in the upper head, since a skull stripping algorithm will by no risk affect the vessels inside the brain. 4.3.1 Gradient based method Even though contrast filled blood vessels and bone suffers from an intensity overlap in the CT-scans, they differ a lot in the way they connect with surrounding tissue. The lumen of the vessels, that contains the contrast agent, is enclosed by three layers of vessel tissue, with the arteries having the thickest walls. This gives the appearance of a gradually decreasing intensity from the lumen out towards the surrounding tissue. Bones on the other hand are more cancellous on the inside, in the marrow, and denser towards the outer (cortical) layers. This can be exploited to find the bones, without including the vessels. The method is based on three steps: 1. Find image edges 2. Distinguish bone edges and fill the insides 3. Improve mask and mask away all bone tissue The first step is done by either using a morphological gradient or calculating the real gradient of the image and converting it to a scalar field. The first is given by first doing a grayscale dilation of the original, from which the grayscale erosion of the original is subtracted. Both these methods are implemented in MeVisLab and appeared to take approximately the same time to calculate, even though the real gradient is a bit faster. During testing, a step length of two voxels outside the current voxel seemed to be a good setting for the gradient calculation. After this step, only the edges of bone, cartilage, vessels and skin are well visible. It is at this stage clear that the bone edges are much more prominent than the rest of the edges. Thus, applying a lower threshold to the gradient image will remove edges that do not belong to bone. Simultaneously, the image is converted to a binary mask, that only contains the edges of bone. A filling filter, also implemented in MeVisLab, can then be used to fill up cavities, i.e., the inside of the bones, consisting mainly of marrow. This however works far form perfectly, since leakages are not prevented. Finally, to make sure that there will not be a thin layer of bone left (even a single voxel thin layer can obscure almost all view), the mask is dilated with a simple 33 cross kernel. The mask can now be used to hide all voxels, in the original volume, that it covers. The vessels are then best visualized with a MIP volume rendering. 4.3.2 Bone registration The problem when trying to find bone is that whatever method is used, it is very difficult to find it all. Parts of marrow and cartilage are likely to be left unfound. As mentioned in section 3.8, one of the newest techniques to do bone subtraction, and mainly skull stripping, is registration. The concept here is to match a correctly segmented bone structure to another patients bone structure by moving, scaling, rotating and distorting it. When the matching is done, the transform can be applied to any mask, used to remove the bone. ITK is well developed for doing registration on multi-dimensional images, but the number of functions and parameters can be frightening to use for someone who has never worked with registration before. Fortunately, it has been made easy with Elastix, mentioned in section 4.1.3. Some things have to be done before Elastix can be used, though. The first step is to have a bone mask. This is the paradoxical problem since a bone mask is the result we want to achieve by doing the registration. So alternatives are to either create a mask by manually masking every slice separately, or to create a rough mask by for instance using thresholding and morphological operations. For this project many different masks were 4.4. COMBINING APPROACHES 29 tested, where the most detailed one was extracted by thresholding a CT volume of a deceased person, with no contrast fluid in the blood vessels. To speed up the registration process, it is possible to use a ROI mask surrounding only the head in the fixed image. This can also contribute to a better end result as lots of information, such as noise around the head can simply be ignored. For the final result, first a registration with only affine transformation was used, followed by a non-rigid B-spline transform registration, using the affine registration output as input. This turned out to be a very time consuming approach. When doing registration on a 512x512x510 voxel volume with a ROI mask around the bone, it still took around 5 minutes to get a final result. This was on a dual CPU computer with 12 cores, clocked to 2.4 GHz, and 32 GB of RAM. The results are not good enough to be used for examination due to the loss of vessel data in many regions. Figure 4.2: The result of doing bone subtraction with the registration approach. Even though this was a nice data set, there are still pieces of bone fragments left, and some vessel data removed. 4.4 Combining approaches It is fully possible to use techniques for both subtracting bone and to find vessels. Stephanie Behrens [20] proposes an approach where most of the bone is first masked away, and the vessels are then extracted with an edge based level-set segmentation. However, what it finally came down to was to do a bone subtraction with some restrictions, inspired by A. Alysassin et al [21]. The basic idea is to, by region growing, do a composite bone mask that contains all the bone in the image, both dense and porous, as well as some of the vessels where the region growing has leaked. The remaining thing to do is to remove the vessel data from this mask. This is done with another region growing from the common carotid arteries, outwards. Now here is the problem: If the first region growing leaks from bone to vessel, the second one will obviously leak from vessel to bone, thus removing too much of the composite mask. This leakage can be limited in the following manner: 30 CHAPTER 4. METHOD AND IMPLEMENTATION 1. Find only the densest bone in the image and create a mask of this. 2. Dilate this mask to make it thick enough. 3. Subtract this mask from the original image where the vessel region growing will be made. If done correctly, this will have created a gap between most of the vessels and porous bone, stopping the leakage. The reason for not doing it in the bone region growing step is that it might create a gap so that the region growing finishes before it can collect all bone. For instance, if a seed point is placed on the top of the skull, the spine might not be included in the composite mask. Instead, in worst case now, there will be pieces of bone still in the final segmentation. The final algorithm works as follows: 1. Create an image, M ID, containing all bone and high intensity vessels (such as the carotid). 2. Create an image, HIGH, containing only the densest bone. 3. Dilate HIGH and subtract it from M ID, giving M ID2 . 4. Create a composite bone mask, Mcomposite , by region growing all bone from the top of the scull. The thresholds have to make sure that all bone is included. This will leak into vessels. 5. Create a restriction mask, Mvessels , by region growing the vessels in M ID2 , and dilate it. 6. Subtract Mvessels from Mcomposite to create a final bone mask, Mbone . 7. Subtract Mbone from the original image and do a region growing on the result from the carotid vessels. Here, the thresholds can go from Imagemin to very large value, for instance 2000 HU. Its only purpose is to remove small pieces of garbage, far from the vessels. This technique was used for the segmentation in the final result images. 4.5. VESSEL ANALYSIS 31 4.5 Vessel analysis In the end of this project I was given a sub-task, namely to extract the contour of a vessel cross cut in 2D, given a center point. Sectra’s software engineers have implemented a centerline tracking algorithm for blood vessels, based on fuzzy connectedness [22]. It allows for segmentation of a single vessel from two chosen points, A to B. Among other things this is used for giving assistance during diagnosis of stenosis. When plaque builds up inside the vessel, the diameter of the lumen decreases. Hence, if the diameter changes drastically over a short section, the chance of stenosis is high. Figure 4.3: Centerline algorithm in Sectra’s internal tool VRTTest. Two mouse clicks are used to place start and stop for the centerline. This can be done either in 3D or 2D. To do this comparison, an MPR (128 x 128 pixels) is created for three part of the centerline, simultaneously, so that every image plane is orthogonal to the centerline direction at that point. Further, another algorithm calculates the contour of the vessel cross cut. Finally, the minimum and maximum diameter of the contour can be derived and compared to the other two contours. The bigger the difference between the minimum diameters, the higher chance of stenosis. Calculating the contour can be done in many ways. Previously, an optimized level-set method has been used to do this. The main demands on the algorithm is that it has to be fast (< 0.1s per image) and it should not leak into adjacent vessels, for instance from an artery into a vein. The first attempt was to use thresholding and labeling, i.e., the MPR would be thresholded into a binary image so that vessel-like pixels would get the value one and everything else zero. Then a labeling algorithm would sort other regions out from the one containing the center point. This approach was naive and worked very poorly, since it required only a single pixel to leak and was also slow due to the many read and write instructions to every pixel. The method was improved quite a bit by implementing a K-means clustering algorithm. This algorithm converged to automatically set thresholds which assigned pixels in the image to separate clusters: lumen, plaque, vessel tissue and other tissue. This made the algorithm more robust, but still had problem with leakage. 32 CHAPTER 4. METHOD AND IMPLEMENTATION The way to go was to use a more simple type of active contour (also known as snake) – an approach where the contour behaves according to several conditions. The contour iteratively converges towards the contour of the vessel lumen. Moreover, what the algorithm does is to give every point on the contour a certain energy depending on the underlying pixel intensity, as well as position compared to its adjacent contour points. This is basically how it works: 1. A contour is initiated as a circle around the given center point. The point positions are stored in an array. 2. For every point, the underlying pixel value is checked. There are three important key values: lumen-to-outside border, Tlow , lumen mean, Tmid , and lumen-to-plaque border, Thigh . The point is given energy according to a function that has its max (1) at Tmid , is zero at Tlow and Thigh and is negative if lower than Tlow or higher than Thigh . 3. The point is also pulled towards its two closest neighbors to make sure that the ”tension” between points strives to be uniform around the whole contour. The farther away two points are from one another, the more powerful the pulling force will be. 4. If the energy, derived from step 2 is positive, the point will move outwards, expanding the contour. If it is negative, the contour will contract. The movement direction of any point is a mix between the direction away from the center point and the normal of the contour at the current point. The normal is given by the vector, which is orthogonal to the vector between a points left neighbor minus its right neighbor. 5. When all points are moved a new center point is calculated, based on the geometrical center of the contour. 6. The area inside the contour is calculated and compared to the area from previous iteration. If the difference is small, the algorithm stops, since the contour hopefully has converged to the lumen contour. 7. The array, holding all points, is returned. The final algorithm adjusts for more than just the above mentioned situations. For instance, sometimes the centerline goes through plaque, which will result in bad center points for certain MPR. If this happens, the movement of the contour will be inverted, which is bad. Therefore, the first thing to examine is if the poorly placed center point can be saved. If the center point value is of plaque, the initialized contour points are checked to see if any of them are outside plaque. If so, the center point is moved there instead – preferably to the point with a value closest to Tmid . If not, it is more desirable to return no contour at all and say that this was a hopeless case, rather than giving an erroneous result. Chapter 5 Results 5.1 Bone subtraction segmentation The following section contains the result achieved with the method described in section 4.4. The method was tried out on several data sets with various results. Not all of them are shown in this report. It is obvious that the better the image is, the better the segmentation will be. Image noise, bad contrast agent distribution and tooth fillings are all lowering the possibility of doing a good segmentation. 34 CHAPTER 5. RESULTS Figure 5.1: Final segmentation of a CT head and neck image, with the combined bone subtraction and vessel finding algorithm. These images are captured from Sectra’s internal tool VRTTest. 5.1. BONE SUBTRACTION SEGMENTATION 35 36 CHAPTER 5. RESULTS Figure 5.2: The same segmentation shown with voxels of lower HU included and excluded respectively. This is good if only either the cerebral vessels or carotid vessels are supposed to be examined. 38 CHAPTER 5. RESULTS Figure 5.4: Segmentation of the carotid and vertebral vessels. The zoomed in figure shows that the patient suffers from stenosis near the carotid bifurcation. 5.2. VESSEL ANALYSIS 39 5.2 Vessel analysis This section holds the results of the 2D vessel segmentation algorithm. Also here, many data sets were used for testing, but not all of them are shown in the result images. Testing indicates that the algorithm certainly works well for most cases, but suffers from problems with heavily varying intensities in the MPR (mostly caused by noise). The exact speed of the algorithm is difficult to establish, partly because it varies a lot depending on the vessel size, partly because it is so fast. Most of the time, a final contour is calculated in the matter of milliseconds. The contour in the following images was calculated with C++ code. Figure 5.5: Successful contour calculation of the common and interior carotid vessel. The lower image shows that the vessel is diagnosed with stenosis with a risk factor of 53-65% 5.2. VESSEL ANALYSIS 41 Figure 5.7: More results showing that the algorithm is capable of segmenting: large, noisy vessels (top); vessels that are very small and close to another vessel (second); highly calcified vessels (bottom two). 42 CHAPTER 5. RESULTS 5.3 Evaluation Since there are few people on Sectra that have extended medical background, it has been difficult to determine if a result is good or not. Also, many people that do have medical background are not used to look at 3D images and might get confused. My main source of evaluation has been Chunliang Wang, employee at Sectra and researcher at CMIV, having both a medical and philosophical doctors degree. According to him, the final results of the vessel segmentation looks good. My other source of evaluation is a doctor in Holland, whom I have not met in person. My results were brought there during a business trip and he meant that the results looked good enough to invest money into. If this segmentation could have been used, more or less automatically, for the last 10 patients that had a CT-scan on the head and neck area, they would have done so. Overall, the registration approach is to slow and does not produce results that are good enough. However, the combined approach with region growing and morphology does produce results that could be used for medical examinations. Sectra mentioned to present this thesis as work in progress and will hopefully develop the method further. Chapter 6 Conclusion 6.1 Discussion Developing tools for medical imaging is very challenging, due to many reasons. First of all, the results have to be very good and reliable. If they are not, doctors might not be able to make a correct diagnosis. Secondly, input images may vary a lot from patient to patient, therefore making some algorithms very parameter sensitive and difficult to automate. As I have stated several times already, it is important to get results that are not misleading. In terms of blood vessel segmentation, this is mainly showing parts of vessels that should not be there, i.e., visualizing the blood vessel lumen thicker than it really is. The reason for this is that the doctors still only use the 3D visualizations as a pre-step in the examination. If they suspect there might be a problem, further investigations will be made based on the pure 2D slices. Removing too much of a vessel is also a problem, though it is not as misleading as removing too little. If a vessel looks thinner than it should, it can easily be confirmed, from the 2D images, whether it really is or not. Having this in mind and comparing the methods of finding the blood vessels themselves and removing the bone, it is possible to draw a conclusion. The first technique involves tracking down either the edge of the vessels in some way or finding their center lines and growing these outwards. But how can we decide if the right amount of vessel is captured during the segmentation? Both the outcome of getting too much and too little is possible. The limit of which within a vessel exists has to be defined during the segmentation process, thus it can be difficult to adjust the results during inspection to see if the border thresholds were chosen well. However, when removing the bone surrounding the vessels, the only way the vessels themselves might be erroneously visualized is if parts of them are masked away together with adjacent bone. Of course we want to keep as much of the vessels as possible, but this method is superior due the fact of two things: Data is never, in any way, added to the final image, only removed. Also, only vessels that are in close proximity to the bone mask risk being partly removed. Just by knowing which vessels are in the risk zone makes it possible to see if they are badly segmented or indeed suffers from stenosis etc. There is obviously the case where there are still pieces of bone tissue left after the segmentation. However, these cases might not even be disturbing, and if they are, they are probably located in an area where it is not as important to investigate blood vessels, compared to the Carotid vessels and inside the brain. I tried to find a way to be able to segment the blood vessels in both head and neck simultaneously. The most difficult part to segment is the lower skull base: the carotid canal etc. As I have learned during this project, this area is not that interesting to look at during a 3D-visualization, due to the difficulties of getting good segmentations results there, which could also explain why there are almost no research on doing segmentation for head and neck simultaneously. One conclusion that I have come to is that if the data set is bad, the result will be bad, no 44 CHAPTER 6. CONCLUSION matter how good your segmentation algorithm is. Bad data can depend on movement from the patient or bad timing with the contrast agent. Unfortunately, this seems to be a quite common problem. If the contrast agent is at wrong position when capturing the image, small vessels will disappear completely. Another big problem is dental restorations. Old dental fillings are made of amalgam, which the x-rays bounce against. The result is a fan like shape with high voxel intensities, around the tooth region.These artifacts can be difficult to remove but fortunately, the blood vessels around this area are not as important as many others. It can still be annoying and obscure the visualization. A problem with the registration approach is that it is initially made for smaller image adjustments, such as to counter patient movements. When doing BSCTA, the patient is first scanned without contrast agent injected into the vessels, and then with it. At that time, the patient will most definitely have moved slightly. The images are therefore aligned with registration before their difference is calculated. But the variation from patient to patient can be huge, both regarding global size, position and noise, but also the inner structure of bone tissue. This can make it difficult to match images from different patient well. A solution to this is to use an atlas of bone masks, proposed in [18]. Unfortunately, I did not have the time to create such an atlas. However, the largest issue is knowing what to mask away after the registration is completed. The derived transform could be applied to any mask, though, if the mask is just a non-detailed blob, it will not matter whether the registration is good or not. The ultimate mask would be a perfect segmentation of all the bone from the patient in the moving image. But this is what we want to achieve by doing a registration in the first hand. So, it is kind of a Catch-22 – the paradoxial situation where we cannot get a segmentation of the bone until we have a segmentation of the bone. Of course, there are ways to get a bone mask, for instance, by manually painting the mask slice by slice. Another way is to extract the mask from an image volume where the patient was scanned without contrast agent in the vessels. In that case, there is no intensity overlap and a simple threshold segments the image as needed. Unfortunately, I only had access to a single CT image of this type. Despite this fact, one should not assume that the registration will be flawless just because the mask is. As said, placement of tissue varies a lot between patients. For instance, there are those who have a lot of space between the vertebral arteries and the vertebras. Others have almost none, which gives the problem where it looks like the arteries and vertebras are one unit. If the first case is matched to the second, the edge of the vertebras might get stretched to also cover the artery, thus removing parts of it during mask application. The confined region growing approach results in some very good segmentations. The algorithm is also very quick. The problem is its lack of automation. For every image that will be segmented, a number of thresholds have to be specified, which in itself is time-consuming. 6.2 Future work Registration is a trendy technique to use for medical image segmentation. The biggest problem, as for now, is that when used for bone removal, the risk of also removing vessels is imminent. Even though it is mostly possible to see if the vessel was removed by the algorithm (and not hidden due to a vascular defect) the result can be misleading. If the registration could be combined with a method to limit the masking, that would be a huge improvement. The second problem is the time it takes to do registration on huge volumes. If the process could be implemented to take advantage of the parallelism in modern graphics processors, the computation time could probably be decreased to only a fraction of that with a CPU. Blood vessel segmentation in head and neck should also probably be treated differently, as H. Shim et al [23] propose with their partition-based extraction of the cerebral arteries. This is 6.2. FUTURE WORK 45 due to the fact that the vessels in the head are not very similar to the ones in the neck. This of course leads to the necessity to find the border between the two regions, which could be future work for this project. Also, to be able to automate the thresholds for the region growing approach would be a huge benefit. Bibliography [1] C. Kirbas and F. Quek, “A review of vessel extraction techniques and algorithms,” ACM Comput. Surv., vol. 36, pp. 81–121, June 2004. [2] O. Wirjadi, “Survey of 3d image segmentation methods,” 2007. [3] O. Cuisenaire, S. Virmani, M. E. Olszewski, and R. Ardon, “Fully automated segmentation of carotid and vertebral arteries from contrast enhanced cta,” pp. 69143R–69143R–8, 2008. [4] M. Freiman, L. Joskowicz, N. Broide, M. Natanzon, E. Nammer, O. Shilon, L. Weizman, and J. Sosna, “Carotid vasculature modeling from patient ct angiography studies for interventional procedures simulation,” International Journal of Computer Assisted Radiology and Surgery, vol. 7, no. 5, pp. 799–812, 2012. [5] H. A. F. G. van Andel, H. W. Venema, G. J. Streekstra, M. van Straten, C. B. L. M. Majoie, G. J. den Heeten, and C. A. Grimbergen, “Removal of bone in ct angiography by multiscale matched mask bone elimination,” Medical Physics, vol. 34, no. 10, pp. 3711–3723, 2007. [6] D. Morhard, C. Fink, C. Becker, M. Reiser, and K. Nikolaou, “Value of automatic bone subtraction in cranial ct angiography: comparison of bone-subtracted vs. standard ct angiography in 100 patients,” May 2008. [7] M. van Straten, M. Schaap, M. L. Dijkshoorn, M. J. Greuter, A. van der Lugt, G. P. Krestin, and W. J. Niessen, “Automated bone removal in ct angiography: Comparison of methods based on single energy and dual energy scans,” Medical Physics, vol. 38, no. 11, pp. 6128–6137, 2011. [8] WikiRadiography, “Hounsfield unit.” http://www.wikiradiography.com/ page/Hounsfield++unit. Online; accessed 2013-04-24. [9] P. Mattsson and A. Eriksson, “Segmentation of carotid arteries from 3D and 4D ultrasound images,” Master’s thesis, Linköping University, SE-581 83 Linköing, Sweden, 2002. LiTH-ISY-EX-3279. [10] Diffen, “Ct scan vs mri.” www.diffen.com/difference/CT_scan_vs_MRI. Online; accessed 2013-04-25. [11] S. Pan and M. Kudo, “Original paper: Segmentation of pores in wood microscopic images based on mathematical morphology with a variable structuring element,” Comput. Electron. Agric., vol. 75, pp. 250–260, Feb. 2011. [12] K. Zhao et al, “Auto-threshold bone segmentation based on ct image and its application on cta bone-subtraction,” Photonics and Optoelectronic (SOPO), pp. 1–5, 2010. BIBLIOGRAPHY 47 [13] B. Bouraoui, C. Ronse, J. Baruthio, N. Passat, and P. Germain, “3D segmentation of coronary arteries based on advanced mathematical morphology techniques,” Computerized Medical Imaging and Graphics, vol. 34, pp. 377–387, 2010. [14] M. Kass, A. Witkin, and D. Terzopoulos, “Snakes: Active contour models,” International Journal of Computer Vision, vol. 1, pp. 321–331, Jan. 1988. [15] S. Grosskopf, C. Biermann, K. Deng, and Y. Chen, “Accurate, fast, and robust vessel contour segmentation of CTA using an adaptive self-learning edge model,” Medical Imaging 2009: Physics of Medical Imaging, vol. 7258, 2009. [16] R. Marcin, “Vessel Detection Method Based on Eigenvalues of the Hessian Matrix and its Applicability to Airway Tree Segmentation,” Oct. 2009. [17] M. Avriel, Nonlinear programming : analysis and methods. Publications, 2003. Mineola, NY: Dover [18] H. A. Kirisli, M. Schaap, S. Klein, L. A. Neefjes, A. C. Weustink, T. Van Walsum, and W. J. Niessen, “Fully automatic cardiac segmentation from 3d cta data: a multi-atlas based approach,” pp. 762305–762305–9, 2010. [19] P. H.-O. Friman O, Hindennach M, “Multiple hypothesis template tracking of small 3d vessel structures,” Medical Image Analysis, pp. 160–171, 2010. [20] S. Behrens, “Automatic level set based cerebral vessel segmentation and bone removal in ct angiography data sets,” 2012. [21] A. M. Alyassin and G. B. Avinash, “Semiautomatic bone removal technique from CT angiography data,” in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series (M. Sonka and K. M. Hanson, eds.), vol. 4322 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, pp. 1273–1283, July 2001. [22] C. Wang and Ö. Smedby, “Coronary artery segmentation and skeletonization based on competing fuzzy connectedness tree,” in Medical Image Computing and Computer-Assisted Intervention MICCAI 2007, vol. 4791 of Lecture Notes in Computer ’ Science, pp. 311–318, Springer Berlin Heidelberg, 2007. [23] H. Shim, I. D. Yun, K. M. Lee, and S. U. Lee, “Partition-based extraction of cerebral arteries from ct angiography with emphasis on adaptive tracking,” in Proceedings of the 19th international conference on Information Processing in Medical Imaging, IPMI’05, (Berlin, Heidelberg), pp. 357–368, Springer-Verlag, 2005.